1.13. Алгоритм цифрового управления по критерию быстродействия

Решение задач оптимизации систем управления по критерию максимального быстродействия использует стратегию, предложенную Л.С. Понтрягиным и его учениками. Однако существует еще и другая проблема - определение моментов и знаков оптимальных управляющих воздействий а также вида переходного процесса при заданных начальных условиях и ограничениях на управляющее воздействие.

Доказано, что оптимальной является стратегия при которой принимает максимальное значение, принадлежит к классу кусочно-непрерывных функций с конечным числом точек разрыва первого рода на конечном интервале времени. При этом теорема об «» интервалах позволяет утверждать, что число переключений управляющего воздействия равно порядку дифференциального уравнения динамической системы.

Сложность определения моментов переключения заключается в том, для каждого момента переключения необходимо знать свои постоянные интегрирования, которые могут быть определены по начальным и конечным условиям для управляемой переменной.

Опыт показывает, что даже для дифференциального уравнения второго порядка, для которого достаточно информации для определения постоянных интегрирования, не всегда можно получить точное решение при определении моментов переключения. Это связано с тем, что необходимо решать систему трансцендентных уравнений, решение которых можно найти только приближенно.

Рассмотрим метод, позволяющий аналитически решить задачу перевода замкнутой системы из одного состояния в другое за конечное число периодов квантования. Не является препятствием для этого и наличие чистого запаздывания. Однако метод распространяется только на линейные динамические модели.

Сущность метода заключается в следующем. По дифференциальному уравнению или передаточной функции линейной динамической системы, задавшись периодом квантования, получают -передаточную функцию системы с фиксатором нулевого порядка .

Период квантования можно выбирать произвольно, но лучше таким, чтобы при максимальном воздействии регулируемая величина достигала - процентов от нового желаемого состояния.

Выберем такой оптимальный цифровой фильтр -того порядка, который обеспечил бы перевод системы за -периодов квантования из начального состояния в конечное (рисунок 1.10).

Практически реализуемые цифровые системы управления имеют конечное время переходного процесса и, следовательно, конечное число шагов или периодов квантования при переходе из одного установившегося состояния в другое. Единичное ступенчатое входное воздействие по заданию является наиболее сложным, поскольку оно имеет разрыв первого рода при , где - безразмерное относительное дискретное время, выражаемое в числе периодов квантования, .

Рисунок 1.10 - Структурная схема цифровой САУ

Можно задать значения переменных системы автоматического управления, изображенной на рисунке для каждого конкретного периода в таком виде:

(1.89)

(1.90)

(1.91)

-преобразование задающей величины имеет вид:

, (1.92)

а для выходной и управляющей:

, (1.93)

. (1.94)

Область применения -преобразования распространяется на непрерывные передаточные функции, число полюсов которых по крайней мере на один больше числа нулей, поэтому .

Разделив зависимости (1.93) и (1.94) на выражение (1.92), получим:

, (1.95)

где ; ; .

,  (1.96)

где ; ; .

Из соотношения (1.95) следует, что

. (1.97)

Передаточная функция замкнутой системы между задающим

сигналом и регулируемой величиной равна:

. (1.98)

Определим из этого выражения передаточную функцию регулятора:

. (1.99)

Из сравнения выражений (1.95) и (1.98), следует, что

, (1.100)

а из сравнения выражений (1.95) и (1.96)

. (1.101)

Таким образом, передаточная функция цифрового регулятора может быть найдена, если подставить значения из зависимости (1.100) и из функции (1.101) в выражение .

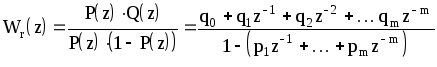(1.102)

Значения коэффициентов регулятора и можно определить из следующих соображений:

. (1.103)

Приравняв коэффициенты при одинаковых степенях числителей и знаменателей, можно заметить, что

; ; .

; ; .

Кроме того, подставив во второе выражение значения и приравняв к единице, находим:

. (1.104)

Таким образом, начальное значение управляющего воздействия определяется суммой коэффициентов объекта полинома числителя дискретной передаточной функции. Известно, что эта сумма убывает с уменьшением периода квантования, поэтому, чем он меньше, тем больше управляющее воздействие. Естественно, что в каждой системе имеется ограничение на управляющее воздействие, поэтому это обстоятельство следует учитывать при расчете цифрового фильтра.

В данной работе предполагаем, что переходный процесс в системе заканчивается за число тактов, равное числу коэффициентов полинома числителя дискретной передаточной функции линейной части. Этот случай справедлив для измерительных систем, работающих в режиме отработки ступенчатого входного сигнала и цифрового регулятора.

Если линейная часть имеет чистое запаздывание , то дискретная передаточная функция, соответствующая ей принимает вид:

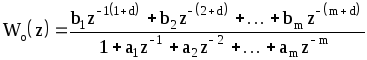, (1.105)

где - целое число периодов квантования, соответствующее

величине чистого запаздывания, .

При этом коэффициенты модели регулятора с передаточной функцией

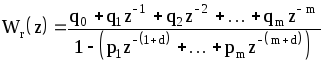(1.106)

должны удовлетворять следующим условиям:

, ;

, ;

Их можно определить из соотношений:

;

; ; ;

=.

; ; ; =.

Таким образом вычисляют коэффициенты передаточной функции оптимального цифрового фильтра.

Зная -передаточную функцию оптимального фильтра можно найти -передаточную функцию замкнутой системы по каналу задание -управляющее воздействие . Вычислив значения управляющего воздействия в каждый из периодов, можно определить моменты переключения оптимального по быстродействию устройства управления.