1.3 Условие устойчивости линейных импульсных систем, описанных разностными уравнениями

Для устойчивой импульсной системы должно выполняться условие

при ,

где

Для того чтобы необходимо, чтобы каждое слагаемое при стремилось к нулю. Это условие будет вы­полнено, если ,

, поэтому

при и .

На комплексной плоскости корни характеристического уравне­ния должны располагаться внутри единичного круга, рисунок 1.7.

Если , то процесс будет монотонным затухающим, если , то процесс будет колебательным.

Если , то система находится на границе устойчивости.

Если , то система неустойчива.

Алгебраический критерий устойчивости импульсных

систем

С помощью замены переменных (дробно-линейного преобразова­ния можно отобразить поверхность единичного круга в плоскости в левую полуплоскость комплексного пе­ременного .

Такое преобразование называется конформным.

Пусть , тогда покажем, что .

Сделав в характеристическом уравнении замену переменных , получим новое характеристическое уравнение, к ко­торому применимы критерии устойчивости Гурвица и Михайлова. Если эти критерии выполняются, то импульсная система устойчива.

Частотный критерий устойчивости импульсных систем,

описываемых разностными уравнениями

Пусть дано характеристическое уравнение импульсной системы

Если известны его корни, то характеристическое уравнение можно переписать в виде

В критерии Михайлова осуществлялась замена в характеристи­ческом уравнении , т.е., вектор скользил по границе устойчивости. Поскольку границей устойчи­вости импульсных систем является круг единичного радиуса, то произведем замену

,

где - угол , а не частота.

Приращение аргумента функции

равно

(1.11)

1. - внутри единичного круга, рисунок 1.3.

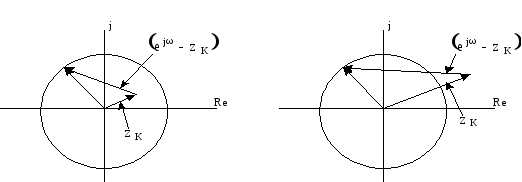
Рисунок 1.3 - Расположение корней характеристического уравнения

В этом случае

2. - снаружи единичного круга, рисунок 1.3,б. В этом случае

следовательно, CAP устойчива, если годограф последова­тельно проходит против часовой стрелки квадрантов при из­менении .

Если

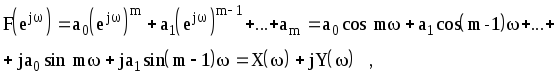
где - четная функция, то, следовательно, - симметричная относительно дей­ствительной оси комплексной плоскости. Это говорит о том, что достаточно изменять в пределах . Поэтому импульсная система будет устойчива, если годограф начинается на вещественней полуоси и поворачивается против часовой стрел­ки на угол при изменении ,

(1.12)

На рисунке 1.4 показаны годографы для устойчивых систем первого, второго и третьего порядка.

1.4 Дискретное преобразование Лапласа

Решетчатая функция получается при модуляции после­довательности мгновенных импульсов единичной площади с периодом повторения сигналом .

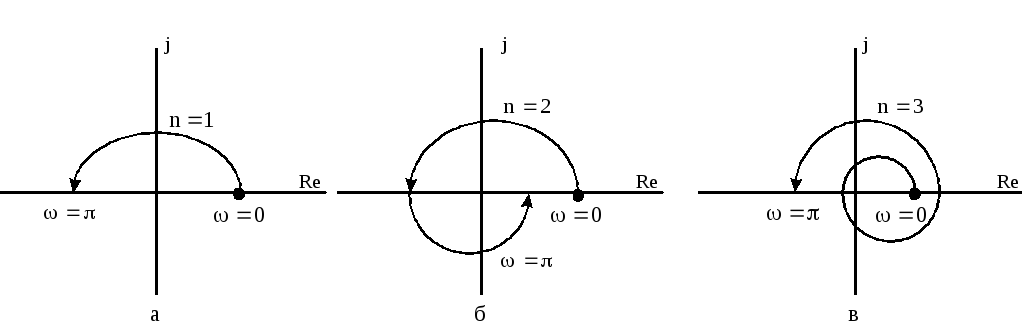
Рисунок 1.4 - Виды годографов устойчивых систем

Действие амплитудно-импульсного модулятора сводится к пе­ремножению , поэтому

, (1.13)

где , - функция Дирака.

Поэтому

,

так как перемножение происходит только в моменты .

Изображение по Лапласу элементарного -того импульса .

Преобразование последовательности импульсов представим в виде

. (1.14)

Изображение решетчатой функции по Лапласу называется диск­ретным преобразованием Лапласа.

.

Для случая, когда в качестве аргумента берется относитель­ное время , выражение для -преобразования принимает вид

, (1.15)

где

параметр дискретного преобразования Лапласа, - относитель­ная частота .

Метод, предложенный Я.3.Цыпкиным, позволяет как и при ана­лизе непрерывных систем ввести понятия о передаточных и частот­ных функциях, а также о частотных характеристиках импульсных систем.

Для смещенной расчетной функции

. (1.16)

Например,

Предел этого ряда - сумма бесконечной геометрической прогрессии

(1.17)

Оператору "" можно в дискретном преобразовании поставить в соответствие выражение .

Поскольку изображение решетчатой функции зависит от , то функция на комплексной плоскости переменной будет периодической вдоль мнимой оси

(1.18)

Оригинал решетчатой функции может быть найден с помощью обратного преобразователя Лапласа

. (1.19)

-преобразование - можно рассматривать как модифика­цию дискретного преобразования Лапласа, использующего подста­новку .

Формула -преобразования получит вид

. (1.20)

Для обратного преобразования

. (1.21)

Такая модификация приводит к тому, что изображение становится функцией переменной , а область устойчивости характеризуется единичным кругом на комплексной плоскости , и -преобразования являются совершенно эквивалентными.