2.3 Стационарные случайные процессы
По степени зависимости статистических характеристик от времени случайные процессы делятся на стационарные и нестационарные.
Стационарным в
широком смысле слова называют процесс
,
математическое ожидание которого
постоянно, а корреляционная функция
зависит только от разности аргументов.
Стационарные
случайные процессы, для которых
статистические характеристики, полученные
путем осреднения по времени одной
реализации в большом интервале времени
приближенно совпадают с характеристиками,
полученными осреднением по множеству
реализаций, называются эргодическими.
Для стационарной эргодичной случайной
функции
при
.
Для эргодического случайного процесса
;
(2.25)
;
(2.26)
.
(2.27)
При
корреляционная функция равна дисперсии
случайной функции
.
(2.28)
Под временем
корреляции понимают интервал времени
,
начиная с которого
и
практически некоррелированы,
.
Для сопоставления корреляционных функций их нормируют,
.
(2.29)
Взаимная корреляция функций двух случайных процессов:
.
(2.20)
2.4 Основные свойства корреляционной функции и спектральной плотности стационарных случайных процессов
Двухстороннее преобразование Фурье корреляционной функции называется спектральной плотностью
;
(2.22)
.
(2.22)
Спектральная плотность является положительной функцией во всем диапазоне частот.
Так как
,
а
- четная функция, то
.
(2.23)
Аналогично
.
(2.24)
и
- четные функции своих аргументов,
.
Если
монотонно убывает, то и спектральная
плотность монотонно убывает.
Чем быстрее убывает корреляционная функция, тем шире спектральная плотность и наоборот.
Наличие колебаний корреляционной функции свидетельствует о наличии периодической составляющей в случайном процессе.
Если
,
то случайная функция содержит постоянную
составляющую «
».
Для центрированной случайной величины
(2.25)
Для взаимной корреляционной функции и ее спектральной плотности справедливы соотношения:
(2.26)
(2.27)
2.5 Прохождение случайных воздействий через линейную сау
Если известна
импульсная переходная функция линейной
САУ
,
то реакция ее на входное воздействие
будет
.
Кроме того, известно, что
.
Найдем связь математических ожиданий
входной и выходной величин линейной
САУ.
,
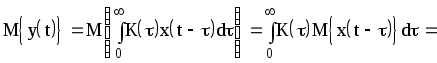
поскольку
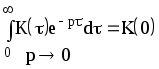- есть коэффициент
усиления линейной части и численно
равен площади импульсной переходной
функции.
Таким образом,
.
(2.28)
Теперь найдем связь между спектральными плотностями входной и выходной величин. Для этого рассмотрим
Здесь
.
Здесь
.
Таким образом,
(2.29)
где
- амплитудно-частотная характеристика
линейной САУ;
- функция, комплексно сопряженная с
.
Зная спектральную плотность входного сигнала, можно определить корреляционную функцию выходного.
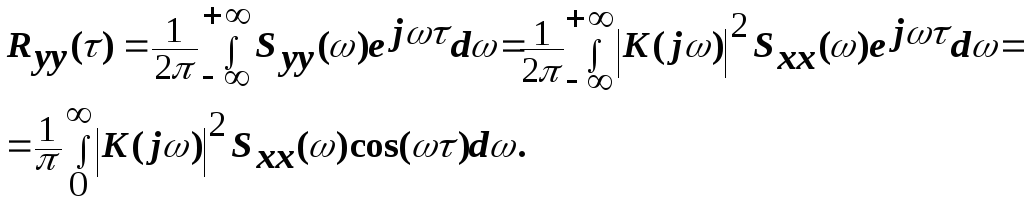(2.30)
Из выражения (2.30) следует, что дисперсия выходной величины равна
.
(2.32)
Пример.
Пусть на вход системы
действует сигнал с постоянной спектральной
плотностью
.
Необходимо найти дисперсию выходного сигнала.
;
.
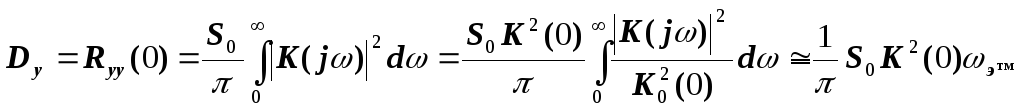- эффективная полоса
пропускания системы, приближенно равна
частоте, при которой
.
Если известна эффективная полоса пропускания системы, а входной сигнал слабо меняется в этом диапазоне, то дисперсию можно приближенно считать по формуле:
.
(2.32)
Найдем связь между спектральной плотностью входного сигнала и взаимной спектральной плотностью входного и выходного.
(2.33)
.
(2.34)
Это позволяет, используя пассивный эксперимент, определять АФХ исследуемой линейной системы.