1.7 Дискретная передаточная функция

Если динамическая система описывается дифференциальным уравнением, то его можно представить уравнением в конечных разностях вида:

.

Используя теорему о смещении решетчатой функции в -преобразовании при нулевых начальных условиях получим:

.

Отношение -преобразования выходной величины к -преоб­разованию входной при нулевых начальных условиях называется дискретной передаточной функцией.

Для статических объектов коэффициент усиления можно найти используя теорему о конечном значении оригинала функции.

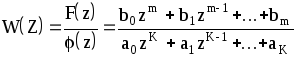; (1.38)

. (1.39)

Для физической реализации алгоритмов вычисления значений решетчатой функции необходимо использовать левые разности, которые учитывают предыдущие а не последующие значения решетчатой функции при вычислении разностей.

;

.

В этом случае передаточные функции будут полиномами в отрицательных степенях. Если имеется передаточная функция с полино­мами, имеющими в положительной степени, то их легко перевести в передаточные функции с отрицательными степенями . Для этого необходимо умножить числитель и знаменатель на Поскольку , то в числителе не может оказаться положитель­ных степеней .

. (1.40)

Системы с астатизмом содержат интегральную составляющую, следо­вательно они имеют полюс при .

. (1.41)

Если на такую систему действует входной сигнал , то уста­новившаяся скорость изменения выходного сигнала будет равна

. (1.42)

Если система имеет чистое запаздывание , , то согласно теореме о сдвиге влево соответствующая импульсная передаточная функция ,

где , - период дискретности.

В итоге дискретная передаточная функция принимает вид: .

1.8 Получение оригинала из уравнений в конечных разностях и с помощью -преобразования

Процедура получения решения уравнения в конечных разностях аналогична процедуре решения дифференциальных уравнений операторным методом. Для этого разностное уравнение с помощью основ­ных теорем преобразуют в алгебраическое.

Пусть имеется разностное уравнение:

.

Подвергая левую и правую часть -преобразованию, получаем:

, или

.

Решаем полученное уравнение относительно изображения иско­мой переменной.

.

Подвергая полученный результат обратному преобразованию, находим оригинал в виде решетчатой функции.

.

В итоге получим линейно изменяющуюся решетчатую функцию.

Получение оригинала по -преобразованию.

-преобразование позволяет легко найти оригинал функции. Это связано с его особенностями, которые объясняются свойствами решетчатой функции. Если - аналитическая функция, то ее можно разложить в ряд Тейлора. Однако, если она имеет изолированные особые точки в виде полюса, то ее можно разложить в ряд Лорана, главная часть которого состоит из конечного числа членов, равного порядку полюса. Для решетчатой функции каждое значение ее есть изолированная особая точка в виде полюса, поскольку представляет интеграл от - функции, имеющей бесконечно большое значение за бесконечно ма­лый интервал и равный значению непрерывной функции в моменты .

Разложим в ряд по отрицательным степеням:

. (1.43)

Поскольку

, если ,

, если ,

то можно вычислить коэффициенты , в разложении , ко­торое называют преобразованием Лорана.

Умножив левую и правую часть равенства (1.42) на , получим:

.

Интегрируя левую и правую часть равенства по замкнутому контуру и учитывая свойства интеграла, получаем:

,

или .

Но , поэтому оригинал решетчатой функции вычисля­ется по формуле:

.

Если полюсы простые, а

, где

, то

. (1.44)

Если полюсы кратные то

,

где - кратность корня,

- число полюсов.

Более простой метод получения по вытекает из разложения ее в ряд Лорана по отрицательным степеням . При этом осуществляется непрерывное деление полинома числителя на полином знаменателя. Это удобно при использовании ЭЦВМ.

Например

Численные значения решетчатой функции на выходе цифровой системы можно получить путем замены -передаточной функции уравнением в конечных разностях.

Пусть передаточная функция цифровой системы

, .

Этой передаточной функции соответствует уравнение в конеч­ных разностях:

,

Разделив коэффициенты на и решив уравнение относительно , получают значения искомой выходной величины че­рез ее значения в предшествующие моменты времени и значения входной величины в соответствующие моменты времени.

По этому уравнению легко реализовать алгоритм вычисления решетчатой функции на выходе цифровой системы при заданном входном воздействии.