1.2 Решетчатые функции и разностные уравнения

Решетчатой называется функция, которую образуют ординаты непрерывной функции , соответствующие дискретным рав­ноотстоящим друг от друга значениям независимой переменной, рисунок 1.2. Она равна нулю, когда и обозначается ;

- период дискретности; - любое целое число.

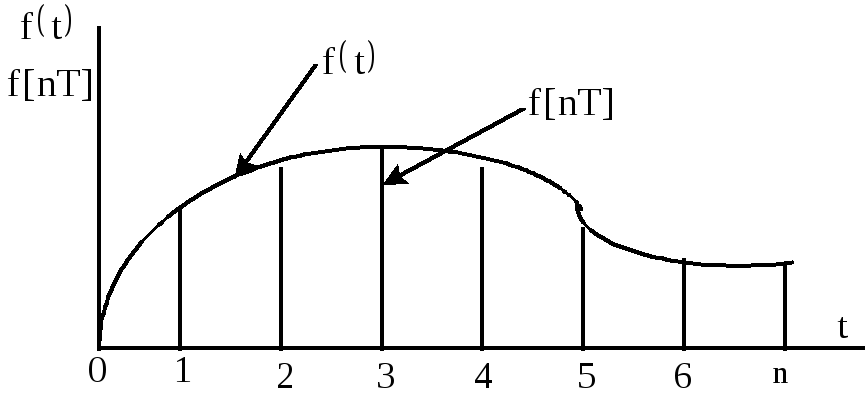
Рисунок 1.2 - Вид непрерывной и решетчатой функции

Для выявления поведения непрерывной функции между дискрет­ными моментами вводят промежуточное фиксированное время , которое может изменяться от до .

Такая функция называется смещенной.

Использовав относительное время, решетчатую функцию запишем , или , где может изменяться в пределах от до .

Скорость изменения решетчатой функции характеризуется ее первой разностью:

.

Разность второго порядка, или вторая разность

,

или

.

Разность -того порядка определяется выражением

, (1.4)

где - биномиальные коэффициенты.

При рассмотрении цифровых систем используются разностные уравнения, определяющие соотношения между дискретной функцией и ее разностями различных порядков . Их можно записать так:

,

или

,

где - известная дискретная функция.

При воздействии на линейную часть прямоугольных импульсов, имеющих разрывы, интегрирование возможно проводить для линейных уравнений только в промежутках времени, где разрывы отсут­ствуют. Это связано с тем, что наличие разрывов приводит к из­менению постоянных интегрирования, которые определяются два ра­за за период. Этот метод построения переходного процесса явля­ется слишком громоздким и возможен для конкретных цифровых рас­четов, исключающих анализ и синтез в общем виде.

Применение разностных уравнений позволяет избежать указан­ных недостатков. Рассмотрим методику получения уравнений в ко­нечных разностях.

Разностное уравнение характеризует связь между переменными, разделенными целым числом периодов. Для возможности проведения анализа всей системы необходимо иметь все уравнения динамики в одной форме (например, в виде разностных уравнений). Найдем уравнение объекта в виде разностного уравнения. Для этого ре­шим дифференциальное уравнение объекта

(1.5)

Пусть ,

тогда ; ; .

Постоянную интегрирования найдем из граничных условий в начале и конце периода.

При

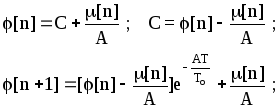
(1.6)

В итоге получили разностное уравнение (1.6).

При решении системы разностных уравнений возникает необхо­димость исключения промежуточных переменных. Это удобно выпол­нять оперативным методом. С этой целью каждую переменную представим в виде ,

где - номер наименьшего периода.

.

В итоге получили алгебраическое уравнение.

При физической реализации алгоритмов управления используют­ся левые конечные разности. Познакомимся с ними в процессе по­лучения уравнения в конечных разностях для дифференциального уравнения второго порядка. Наиболее простым способом получения уравнений в конечных разностях по дифференциальным является метод замены производных соответствующими разностями.

В рассматриваемом случае порядок, дифференциальных уравне­ний второй, поэтому используя соотношения:

(1.7)

Дифференциальное уравнение можно записать через конечные раз­ности, например:

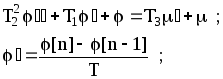
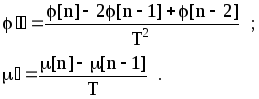
Подставив значения , , , получим:

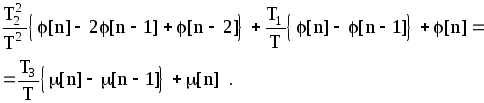
Приведя подобные члены и сделав обозначения:

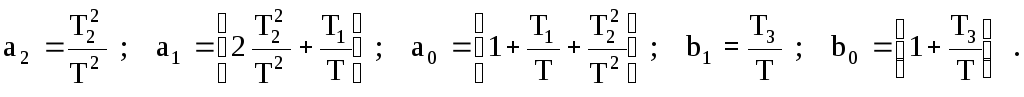
получаем

(1.8)

Второй метод получения уравнений в конечных разностях при­ближенный. Он тем точнее, чем меньше . Для уравнения (1.5) при использовании второго метода легко получить уравнение в конечных разностях, которое имеет вид

(1.9)

Если сравнить выражение (1.6) и (1.9), то мы увидим, что они отличаются друг от друга, поскольку (1.9) является прибли­женным, а (1.6) - точным. Приближенность (1.9) объясняется тем, что мы фактически используем для решения исходного дифференци­ального уравнения численный метод интегрирования.

Если разложить коэффициенты при и выраже­ния (1.6) в ряд Маклорена и удержать только два первых члена, то

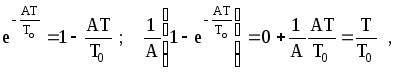
т.е. коэффициенты (1.9) являются первым приближением коэффици­ентов (1.6) при разложении их в ряд Маклорена в окрестности точки .

Второй способ более универсален, поскольку не требует зна­ния правой части дифференциального уравнения и его решения.

Решение разностных уравнений

Линейные импульсные системы описываются линейными разност­ными уравнениями с постоянными коэффициентами. Они подчиняются принципу суперпозиции, поэтому их полное решение состоит из сум­мы решений однородного и неоднородного уравнения.

Пусть дано однородное уравнение

где - номер текущего периода (аналог времени );

- порядок разностного уравнения.

Составим характеристическое уравнение, введя оператор

,

Отсюда характеристическое уравнение принимает вид

Решение однородного уравнения находим в виде

(1.10)

где - корни характеристического уравнения.

- постоянные коэффициенты, определяемые по начальным условиям для решения неоднородного уравнения.

Если имеет -тую кратность, то решение запишем в виде

Частное решение неоднородного разностного уравнения находим в форме правой части (аналогично обыкновенным дифференциальным уравнениям).

Если - правая часть, то, когда не совпадает ни с одним корнем, частное решение записывается в виде

если совпадает с одним из корней кратности "" то