2.8 Фильтр Винера - Колмогорова

Фильтр Винера - Колмогорова (2942 - 2942 гг.) позволяет получить минимальную дисперсию ошибки путем преобразования входного сигнала в выходной , рисунок 2.3.

(2.52)

Рисунок 2.3 - Расчетная схема фильтра

Используя характеристики случайных воздействий, получаем:

(2.52)

Это уравнение называется уравнением Винера - Хопфа - Колмогорова.

- весовая функция фильтра может быть получена в результате решения интегрального уравнения, которое основано на классических методах преобразования Фурье и известного как метод спектральной факторизации, применение которого возможно только для стационарных процессов. Оценки можно найти только после того, как найдена функция веса, т.е. ее нельзя получить в темпе работы системы, что ограничивает область применения метода.

Всякая измеренная величина наряду с полезным сигналом содержит случайную помеху . Задача фильтрации состоит в том, чтобы возможно лучше отделить полезную составляющую общего сигнала от помехи . С этой целью необходимо убедиться в стационарности случайных процессов и , найти их статистические характеристики: математическое ожидание, дисперсию, корреляционную функцию, спектральную плотность. На основании полученной информации необходимо найти такую динамическую систему, которая бы обеспечила минимальную разницу между полезным сигналом и сигналами на выходе фильтра.

Импульсная переходная функция динамической системы будет оптимальна, если обеспечит условие:

(2.53)

Разность полезного сигнала и сигнала, прошедшего фильтр, , содержит две составляющие: -погрешность от частичного прохождения помехи через фильтр; - погрешность от искажения формы полезного сигнала при прохождении фильтра. Задача фильтрации заключается в минимизации суммарной погрешности и, как правило, является компромиссной задачей.

Обозначим тогда .

Спектральные плотности составляющих ошибки определяются так:

Спектральная плотность ошибки на выходе фильтра равна сумме составляющих:

Поскольку , то результирующее значение спектральной плотности можно вычислить так:

Поскольку , а средний квадрат ошибки

, то, минимизируя по и , приходим к следующей системе уравнений:

Из выражения для первой частной производной следует, что при .

Учитывая это соотношение можно записать из выражения для второй частной производной:

(2.54)

В этих выражениях звездочки обозначают оптимальные значения переменных. Если удается реализовать фильтр с оптимальными параметрами, то спектральная плотность ошибки может быть определена по формуле:

(2.55)

Из полученного выражения следует, что, если спектры полезного сигнала и помехи не перекрываются, то в интервале частот, где , а и на всем интервале частот, при которых .

Рисунок 2.4 - Графики спектральной плотности

Таким образом, если полезный сигнал и помеха имеют один и тот же спектр частот, то нельзя получить спектральную плотность ошибки меньше: .

Литература

1 Пугачев В.И. Методические указания и программы расчета основных

характеристик систем автоматического управления. Краснодар, Изд.

КубГТУ, 1996, - 77с.

2 Изерман Р. Цифровые системы управления. - М.:Мир,1984г.-541 с.

3 Куо Б. Теория и проектирование цифровых системы управления.

- М.: Машиностроение, 1986, - 447 с.

_{ПРИЛОЖЕНИЕ}

_{Пример расчета замкнутой стохастической системы с использованием пакета Mathcad}

_{Рассмотрим систему, изображенную на рисунке 1.2. Пусть передаточные функции остались прежними, а параметры САУ имеют конкретные значения:}

_{, , , .}

_{, .}

_{, .}

_,

_.

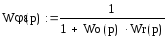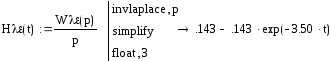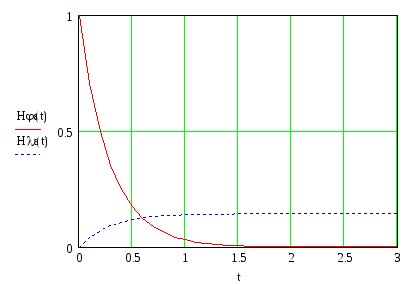
Переходные функции замкнутой системы по каналам: задание – ошибка управления ( и возмущение – ошибка управления (

_{, ,}

Как видно из графиков, в системе имеет место статическая ошибка по каналу – возмущение – ошибка управления.

Интегральные квадратичные оценки при единичном входном воздействии можно найти непосредственным интегрированием:

_{, .}

_{, .}

_{Для определения дисперсии ошибки при произвольном случайном входном воздействии используем частотные характеристики замкнутой системы по соответствующим каналам.}

_{Примем: , ,}

_{, , ,}

_,

_,

_,

_,

_,

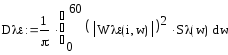_{, , ранее ().}

_{, , ранее ().}

Как видно из расчетов, результаты получились близкими к предыдущим.

Графики амплитудно-частотных характеристик замкнутой системы по каналам: задание – ошибка управления ( и возмущение – ошибка управления (

_{К сожалению, полученные аналитические результаты не всегда можно применить в реальных условиях. Дело в том, что минимальная дисперсии ошибки управления может иметь место при неустойчивой системе. Это обстоятельство заставляет минимизировать дисперсию ошибки при дополнительном условии – заданной относительной степени затухания переходного процесса. При этом на линии равной степени затухания в качестве рабочей точки берут точку с максимальным отношением Кр/Ти (а не правее максимума, как для детерминированных систем).}

_{Для рассматриваемого случая:}

_{, .}

_{Очевидно, что при отрицательном коэффициенте усиления замкнутая САУ будет неустойчива.}

_,

_,

_,

_.

_{, ,}

_,

_{, ,}

_,

_,

Итак, при Кр = 7: ,

при _:

.

Таким образом, использование Mathcad позволяет легко производить расчеты стохастических параметров систем управления.

97