2.7 Синтез сау при заданной структуре

Постановка задачи такова: даны статистические характеристики случайных воздействий , структура системы и все передаточные функции, указаны настроечные параметры . Необходимо найти оптимальные значения , обеспечивающие минимум выбранного критерия качества

, .

Последовательность решения данной задачи такова.

Находят зависимость дисперсии или СКО от варьируемых параметров, используя табулированные интегральные соотношения (2.33), (2.34).

Приравнивая нулю частные производные по искомым переменным, получают систему алгебраических уравнений с неизвестными:

;

. . . . . . . . .

.

Решая совместно систему уравнений, находят параметры системы , обеспечивающие экстремум .

Если необходимо найти , то методика остается прежней, изменяется только система уравнений, которая принимает вид:

;

. . . . . . . . . . . . . . . . .

.

Решая полученную систему уравнений, находят оптимальные значения .

Если квадратичная форма

является положительно определенной, то точке соответствует минимум, если отрицательно определенной, то максимум функции.

В соответствии с критерием Сильвестра квадратичная форма будет положительно определенной, если

; и т.д.

и отрицательно определенной, если

; и т.д.

Здесь

;

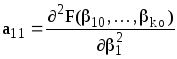и т.д.

;

Пример.

Пусть система состоит из регулятора (рисунок2.2) с и объекта с . Возмущение действует на вход регулятора.

Определить , при котором .

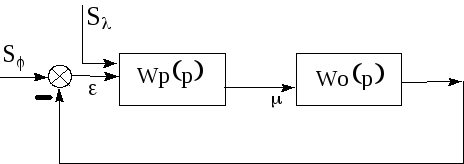
Рисунок 2.2 - Структурная схема САУ

Решение задачи осуществляется в следующем порядке:

Находятся выражения передаточных функций замкнутой системы по соответствующим возмущениям и .

;

; ;

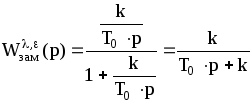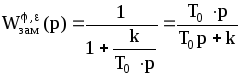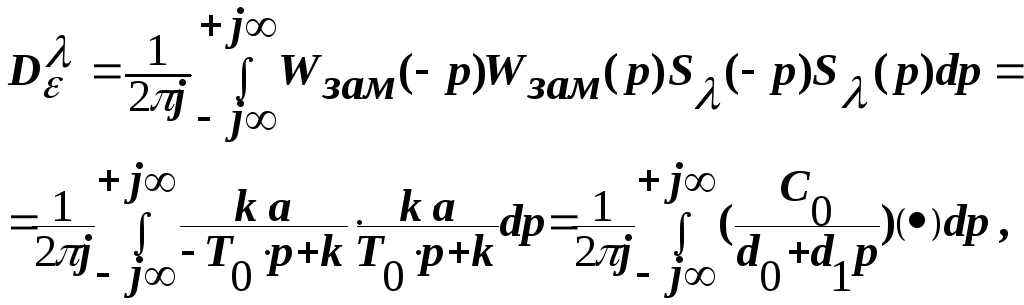
где - обозначен сопряженный множитель.

Степень знаменателя , поэтому

,

где

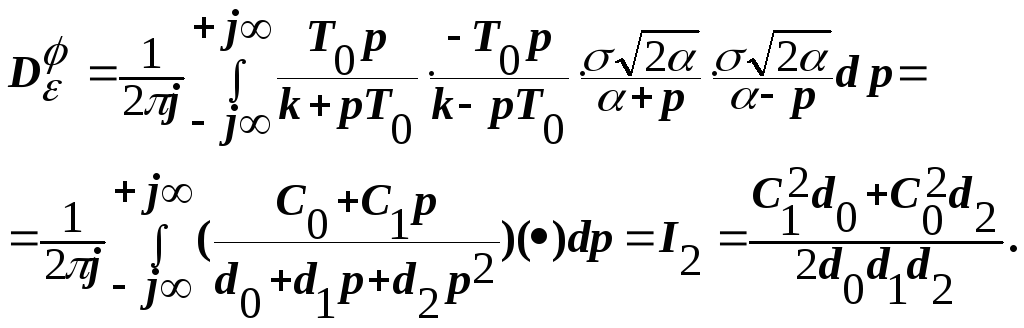
Здесь, как и раньше, пустая скобка под интегралом обозначает сопряженное выражение.

.

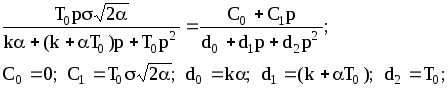
Таким образом,

;

;

.

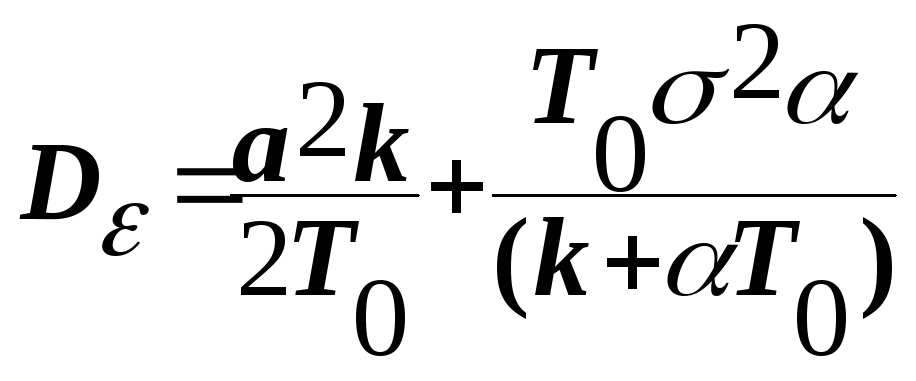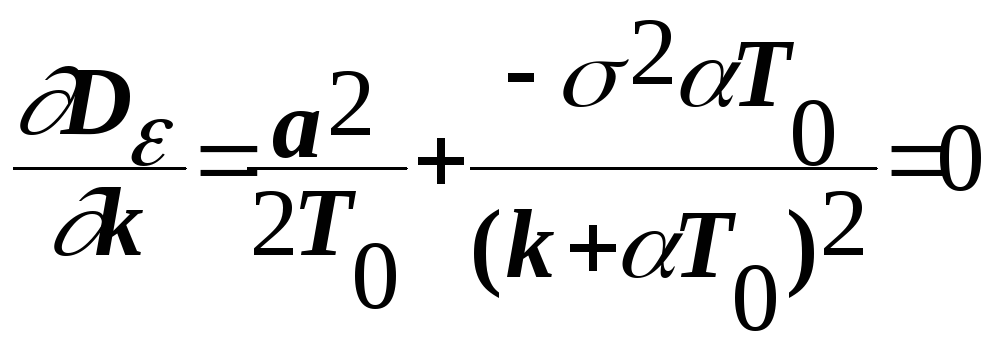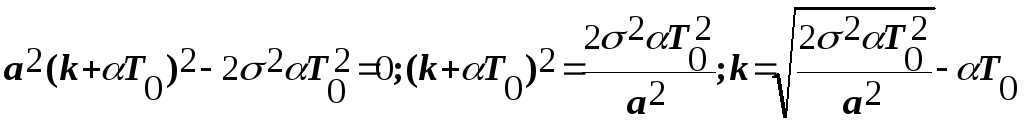Отсюда

.

Легко видеть, что , следовательно, оптимальное значение коэффициента усиления регулятора минимизирует дисперсию ошибки.

В случае сложных выражений для и аналитическое определение оптимальных параметров может быть затруднено. В это случае пользуются приближенным способом, по которому строят графики спектральных плотностей, квадрата модуля АФХ. Перемножая их и суммируя, находят дисперсию ошибки.

Как и при детерминированных входных воздействиях (ступенчатое, импульсное) по реакции на них судят о свойствах линейной системы, так и при случайных воздействиях можно судить о фильтрующих ее свойствах по реакции на единичный белый шум. Это обстоятельство существенно облегчает анализ линейных систем (их сравнение) при наличии случайных воздействий. Конечно, каждая система по-разному будет реагировать на случайные воздействия различного спектра, однако часто можно сказать, что лучше система та, у которой СКО на единичный белый шум меньше.

Вычисление дисперсии в этом случае сводится к оценке интервала

где

Степень полинома числителя должна быть по крайней мере на единицу меньше степени полинома знаменателя.

Разложим полином на четные и нечетные члены:

,

где ; .

Определим следующие отношения:

;

;

где ; ;

; .

Обозначим

Очевидно . Доказана теорема, что если корни полинома лежат в левой полуплоскости, то справедливо рекуррентное соотношение:

В итоге можно получить:

Следует отметить, что рассмотренные задачи в настоящее время легко решаются с помощью математического пакета Mathcad [7].