2.6 Анализ систем регулирования при стационарных случайных воздействиях

Пусть на вход объекта (рисунок 2.1) с передаточной функцией , как по каналу управления , так и по каналу возмущения , действует возмущение:

, (2.35)

где - математическое ожидание возмущающего воздействия, - центрированное значение возмущающего воздействия.

Рисунок 2.1 - Структурная схема САУ

Кроме того, на вход регулятора с передаточной функции подается задающее воздействие в виде:

, (2.36)

где - помеха по каналу задания, ; - полезная составляющая задающего воздействия.

Под ошибкой управления САУ будем понимать величину

, (2.37)

где - случайная функция,

. (2.38)

При стохастическом анализе САУ ее точность может быть оценена по различным критериям:

- по математическому ожиданию , являющемуся систематической погрешностью;

- по дисперсии , т.е. оценке случайной ошибки ;

- по среднему квадрату ошибки (СКО) системы.

Для замкнутой САУ сигнал ошибки в операторной форме равен:

. (2.39)

Отсюда следует, что математическое ожидание ошибки

. (2.40)

Анализ выражения (2.26) показывает, что от систематической ошибки легко избавиться, подав на соответствующие входы сигналы и соответствующих знаков и величин.

, (2.42)

где - корреляционная функция ошибки; - спектральная плотность ошибки.

При оценке качества САУ на основе минимума СКО определяется математическое ожидание квадрата ошибки или СКО системы:

; (2.42)

. (2.43)

Средний квадрат ошибки объединяет математическое ожидание и дисперсию и характеризует качество САУ в целом. При СКО равен ее дисперсии. Ограничиваются оценкой дисперсии в том случае, когда математическое ожидание ошибки мало. СКО нашел широкое применение в задачах синтеза, так как только для критерия минимума СКО задачи синтеза решается аналитически. Если ошибка не должна выходить за определенные пределы, то СКО пользоваться нельзя так как он учитывает с одинаковым весом и большие и маленькие ошибки и не фиксирует отклонения выше допустимых.

СКО, обусловленный стационарными случайными воздействиями, может определяться как с помощью корреляционных функций, так и спектральных плотностей.

Для рассматриваемой системы спектральная плотность ошибки

.

В этом выражении неизвестны и . Их можно вычислить, проанализировав соответствующие сигналы и найдя корреляционные функции. 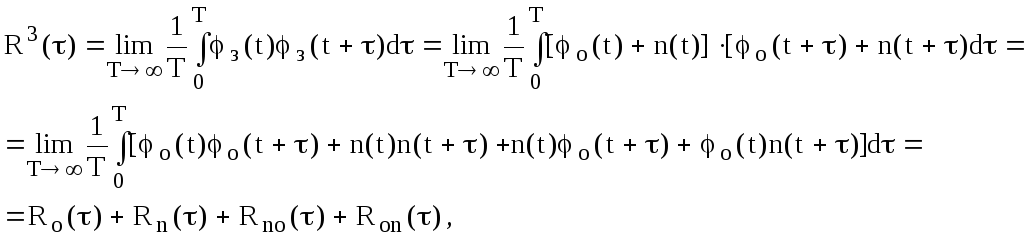(2.44)

где и - взаимные корреляционные функции полезного сигнала и ошибки; и - автокорреляционные функции.

Используя формулу (2.22), связывающую корреляционную функцию и спектральную плотность, получаем:

. (2.45)

Если помеха не коррелированна с полезным сигналом, то

, поэтому

. (2.46)

Для регулярного сигнала , поэтому . Аналогично находится .

Дисперсия сигнала ошибки определяется по выражению:

. (2.47)

Вычисление интеграла вида осуществляется следующим образом.

Преобразуют интеграл и приводят к табличному виду. Известно, что есть дробно-рациональная функция с вещественными коэффициентами,

,

где - есть функция комплексно сопряженная с функцией . Аналогично можно поступить и с .

Например, .

На этом основании искомый интеграл представляем в виде:

,

или, заменив , получим

.

Этот интеграл табулирован, причем

, (2.48)

где ; ;

; (2.49)

; (2.50)

и т.д.

Пример.

Для системы изображенной на рисунке 2.2, предположим , а .

.

Предположим, пропорциональный регулятор и интегрирующий объект имеют передаточные функции

; .

Помеха и действуют по одному каналу, поэтому

;

;

;

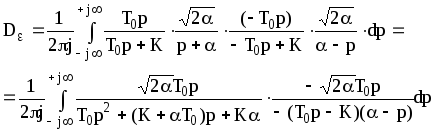
Для полиномов числителя и знаменателя, записанных в виде сопряженных множителей, находим:

; ; ; ; ;

.

Если на систему действует одновременно и , то результирующая дисперсия будет равна сумме дисперсий от каждого возмущения.