2.2 Характеристики случайных процессов

Случайной функцией некоторой независимой переменной называют функцию, значение которой является случайной величиной. Если независимой переменной является время , случайная функция называется случайным или стохастиче­ским процессом. Функция, полученная в результате опыта неслучайна, поскольку закон ее известен. Случайность проявляется в непредсказуемости результатов другого опыта. Совокупность всех реализаций (результатов опыта) представляют случайную функцию или процесс. Для характе­ристики случайных процессов служат моменты случайной функции или ее многомерные функции распределения вероят­ности и плотности вероятности.

Функцией распределения вероятности (интегральный закон распределения) называют вероятность того, что случайная величина примет значение меньше некоторого фиксированного значения

(2.2)

где - символ вероятности.

Соответственно одномерная плотность вероятности есть производная от функции распределения вероят­ностей

. (2.2)

Величина показывает ве­роятность того, что случайная величина находится в интервале до . Если рассмотреть пару значений , полученных в момент времени и , то двумерный закон распределения вероят­ности

, (2.3)

выражает вероятность того, что в момент времени , а в момент времени .

Двумерная плотность вероятности может быть определена так:

.

Она показывает вероятность того, что в момент времени значение случайного процесса находится в пределах , а в момент - в пределах .

Значение , взятые в различные моменты времени

независимы друг от друга. Вероятность совпадения собы­тий, заключающихся в нахождении и между и , в момент времени и между и в момент времени равна произведению вероятностей каждого из этих собы­тий, поэтому

Хотя многомерные законы распределения случайных про­цессов полнее характеризуют процесс, но они громоздки, с ними трудно работать. На практике пользуются одно - или двумерным законом распределения. Например, марковские процессы полностью характеризуются двумерным законом (двумерной плотностью вероятности). Вероятность нахожде­ния в заданном интервале от до в момент зависит только от состояния в предшествующий момент и не зависит от состояния в другие ранее предшествую­щие моменты.

Свойства плотности распределения вероятности:

.

Математическим ожиданием случайной величины на­зывается среднее значение бесконечного множества реали­заций , вокруг которого группируются все реализации данного процесса. Это неслучайная величина (функция).

. (2.4)

называется центрированной случайной функ­цией, .

Для практических расчетов используется формула

. (2.5)

Здесь не истинное значение, а оценка из-за конеч­ного значения ;

- значение случайной функции -й реализации в момент времени .

Степень разброса реализаций относительно харак­теризуется дисперсией случайного процесса, являющейся неслучайной и неотрицательной функцией

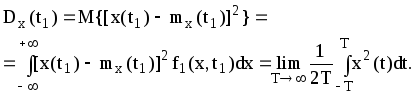(2.6)

Среднеквадратическое отклонение - СКО равно

.

В общем случае и являются функциями времени и определяются для каждого момента как средние по множе­ству

, (2.7)

где - число реализаций, берется для получения не­смещенной оценки, которая исключает систематическую по­грешность из-за использования не истинного значения математиче­ского ожидания, а его оценки .

Связь между значениями случайного процесса в раз­личные моменты времени устанавливается с помощью корре­ляционной функции, определяемой как математическое ожидания произ­ведения значений центрированной случайной функции, взя­той для двух моментов времени и :

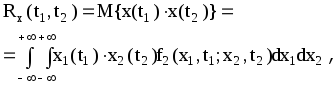(2.8)

где - двумерная плотность вероятности.

При .

Здесь мы опускали точки над случайной функцией, предпо­лагая ее центрированное значение.

Основные свойства корреляционной функции:

является четной функцией, .

не зависит от аддитивной детерминированной со­ставляющей в случайном процессе.

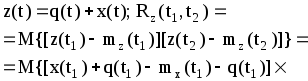
. (2.9)

где - центрированная случайная величина.

Если в случайный процесс детерминированная функция входит сомножителем, то его корреляционная функция опре­деляется выражением:

, ;

(2.20)

Взаимной корреляционной функцией случайных функций и является математическое ожидание произведения эти центрированных функций, взятых в различные моменты времени и .

(2.22)

Взаимная корреляционная функция не обладает свойством симметрии относительно аргументов (не является четной).

.

Если случайная функция состоит из суммы двух некоррелированных (несвязанных, независимых) случайных функций, то выполняется условие:

, (2.22)

где .

Для математического ожидания справедливы соотношения: математическое ожидание суммы случайных функций равно сумме математических ожиданий каждой из них

; . (2.23)

если случайная функция имеет в качестве сомножителя детерминированную функцию, то

, (2.24)

где .