
- •Гоу впо Кубанский государственный технологический университет
- •Печатается по решению Редакционно-издательского совета КубГту
- •1 Цифровые системы управления
- •1.1 Способ управления с помощью эвм
- •1.2 Решетчатые функции и разностные уравнения
- •1.3 Условие устойчивости линейных импульсных систем, описанных разностными уравнениями
- •1.4 Дискретное преобразование Лапласа
- •1.5 Определение периода квантования при дискретном измерении без потери информации непрерывного сигнала
- •1.6 Основные свойства -преобразования
- •1.7 Дискретная передаточная функция
- •1.8 Получение оригинала из уравнений в конечных разностях и с помощью -преобразования
- •1.9 Цифровые аналоги типовых законов управления
- •1.10 Анализ цифровых систем управления
- •1.11 Анализ устойчивости цифровых систем.
- •1.12. Аналитический синтез алгоритма управления цифрового вычислительного устройства
- •1.13. Алгоритм цифрового управления по критерию быстродействия
- •1.14 Особенности реализации цифровых законов управления при использовании сервомоторов постоянной скорости
- •2.2 Характеристики случайных процессов
- •2.3 Стационарные случайные процессы
- •2.4 Основные свойства корреляционной функции и спектральной плотности стационарных случайных процессов
- •2.5 Прохождение случайных воздействий через линейную сау
- •2.6 Анализ систем регулирования при стационарных случайных воздействиях
- •2.7 Синтез сау при заданной структуре
- •2.8 Фильтр Винера - Колмогорова
1.14 Особенности реализации цифровых законов управления при использовании сервомоторов постоянной скорости
Широкое распространение при автоматизации производственных процессов имеют цифровые системы, использующие в качестве исполнительного механизма сервомотор постоянной скорости. Расчет таких цифровых систем является не простой задачей. Это связано с тем, что в системах управления, использующих сервомоторы постоянной скорости нельзя обеспечить амплитудно-импульсную модуляцию из за ограничений на величину управляющего сигнала а также частого отсутствия фиксаторов нулевого или других порядков.
Наиболее распространенным вариантом реализации управляющих воздействий является вариант, при котором роль фиксатора нулевого порядка выполняет выходной триггер, включающий пусковую аппаратуру электрического исполнительного механизма постоянной скорости. При этом изменяется не амплитуда выходного сигнала цифрового регулятора, реализуемого алгоритмически, а длительность включения выходного триггера.
Строго говоря, замена амплитудно-импульсной модуляции первого рода широтно-импульсной, применение сервомотора постоянной скорости переводит рассматриваемую систему из класса линейных в класс нелинейных цифровых систем.
Практика внедрения систем управления и инженерных методов их настройки требует рекомендаций по их расчету и сравнительному анализу с идеальными моделями систем, подлежащих аналитическому исследованию, дающему приближенные результаты, удовлетворяющие практику.
Рассмотрим ПИД- закон регулирования с независимыми параметрами настройки, описываемый уравнением:
![]() (t)=k
(t)=k![]() (t)+
(t)+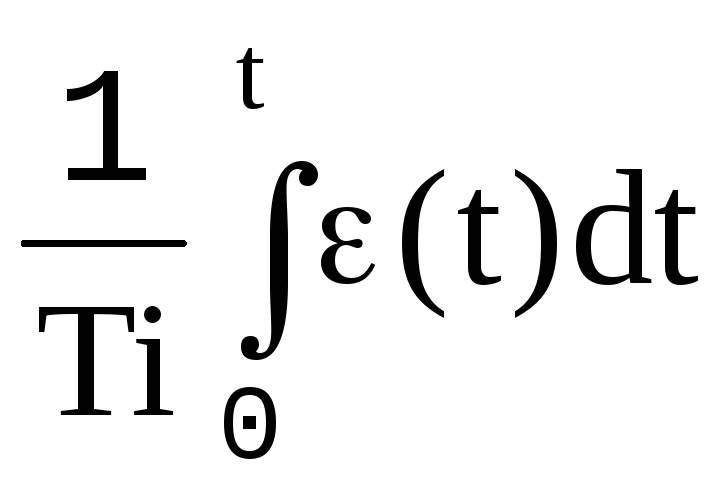 +Tg
+Tg![]() ,
(1.107)
,
(1.107)
где
![]() (t)-
перемещение регулирующего органа,
(t)-
перемещение регулирующего органа,
Ti - постоянная времени интегрирования регулятора,
Tg - постоянная времени дифференцирования регулятора,
![]() (t)-
ошибка управления.
(t)-
ошибка управления.
Обозначив период дискретизации через Т и преобразовав интегро-дифференциальное уравнение в уравнением в конечных разностях, используя замену процедуры интегрирования процедурой суммирования по методу трапеций, получим:
![]() ,
(1.108)
,
(1.108)
где n- текущее дискретное время, n=t/T, n=0,1,2,...,
 .
(1.109)
.
(1.109)
Для цифрового регулятора, описываемого рекуррентным уравнением в конечных разностях (2), переходная функция имеет вид:

Рисунок 1 -График переходной функции идеального цифрового ПИД- регулятора
Как следует из выражения (2), значения управляющего воздействия в дискретные моменты времени будут равны:
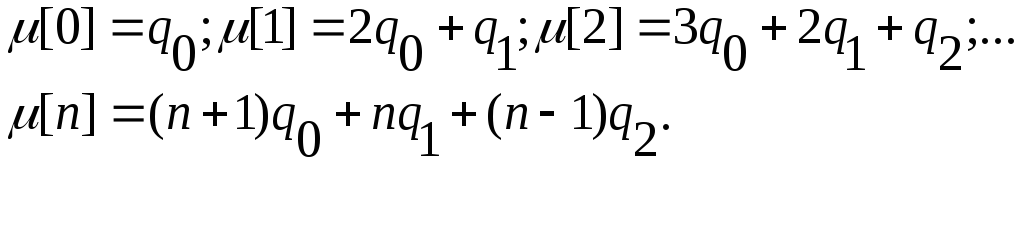
Если учесть то обстоятельство, что управляющее воздействие сдвинуто на такт относительно ошибки управления, то передаточная функция регулятора должна иметь вид:
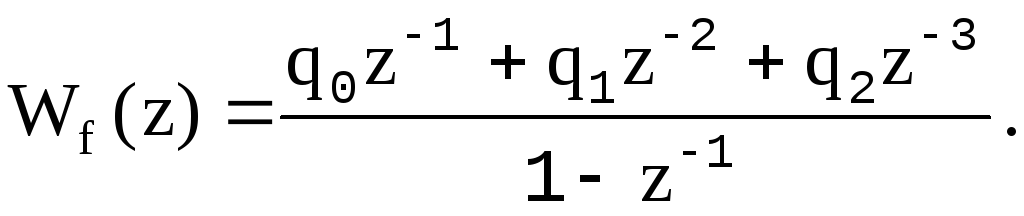 (1.10)
(1.10)

Рисунок 2- График переходной функции реального цифрового ПИД- регулятора
Для расчета цифровой системы управления не имеет значения место задержки сигнала на такт, поэтому его можно отнести к объекту управления, предполагая закон управления идеальным (без сдвига).
Программная реализация закона управления должна проводиться с учетом ограничения на величину управляющего воздействия, что эквивалентно уменьшению общего коэффициента усиления цифрового фильтра и не должна приводить к потере устойчивости. Проверка устойчивости должна проводиться при отсутствии ограничения на управляющее воздействие.
Поскольку уравнение динамики исполнительного механизма с постоянной скоростью перемещения имеет вид
 ,
то это приводит к необходимости
исследования нелинейной системы.
,
то это приводит к необходимости
исследования нелинейной системы.
Цифровой фильтр воздействует на исполнительный механизм постоянной скорости, работающий в режиме включений и отключений при компенсации возмущений и перемещающийся в одну и ту же сторону, т.е. в скользящем режиме. Это обстоятельство позволяет рассматривать его как идеальное интегрирующее звено с z-передаточной функцией, которую легко получить из соотношений:
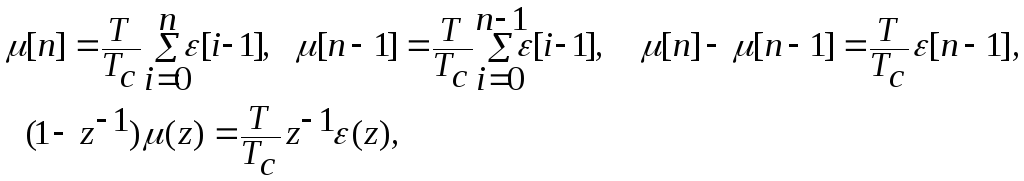
 (1.111)
(1.111)
Результирующая передаточная функция цифрового фильтра совместно с исполнительным механизмом (цифрового закона управления) будет иметь вид:
 (1.112)
(1.112)
Здесь коэффициенты g0, g1, g2 учитывают постоянную времени сервомотора Tс:
![]() (1.113)
(1.113)
Если цифровой фильтр реализует ПИ -закон управления, то общая передаточная функция закона управления совместно с сервомотором постоянной скорости будет:
 (1.114)
(1.114)
Здесь
![]() (1.115)
(1.115)
В процессе реализации цифрового управления при наличии сервомотора постоянной скорости следует учитывать следующие обстоятельства:
1) для реализации закона управления необходимо ставить сглаживающий фильтр (например, методом скользящего среднего) ошибки управления и использовать сглаженные значения;
2) релейный триггер, включающий исполнительный механизм, должен иметь достаточную зону нечувствительности, чтобы исключить появление автоколебаний в системе управления;
3) минимальное время включения исполнительного механизма должно обеспечивать перемещение сервомотора на 1-2 процента его максимального хода;
4) период дискретности Т следует выбирать таким, чтобы в режиме нормальной работы компенсация возмущений проходила включениями исполнительного механизма на время не превышающее 0,5Т.
Как следует из передаточной функции закона регулирования (1.112), получен астатизм 2-го порядка, что может привести к неустойчивой работе системы или снижению ее запаса устойчивости. Для исключения этого обстоятельства в системах стабилизации следует вводить сигнал обратной связи по положению исполнительного механизма или цифровым фильтром реализовать ПД -закон управления.
В последнем случае передаточная функция цифрового фильтра равна:
![]() (1.116)
(1.116)
где q0
= (k+![]() );
q1
= -
);
q1
= -![]() ).
(1.117)
).
(1.117)
Передаточная функция цифрового закона управления при этом принимает вид:
![]() (1.118)
(1.118)
Здесь
![]() (1.119)
(1.119)
Сдвиг на два такта можно отнести к объекту, а регулятор считать идеальным пропорционально-интегральным. Действительно, по формуле (1.118) можно записать уравнение в конечных разностях для случая отсутствия запаздывания:
![]() (1.120)
(1.120)
Принимая нулевые начальные условия, получаем:
![]() (1.121)
(1.121)
Реализация ПД- закона цифровым фильтром совместно с сервомотором постоянной скорости обеспечивает результирующий ПИ-закон управления, соотношения коэффициентов которого с коэффициентами непрерывного регулятора равны:
![]() (1.122)
(1.122)
Здесь Kp и Tii – параметры эквивалентного непрерывного ПИ-регулятора.
Очевидно, что при реализации цифровым фильтром «П»- закона управления, общий закон регулирования будет интегральный:
![]() ,
где
,
где
![]() (1.123)
(1.123)
Возникает вопрос, а можно ли отнести сервомотор к объекту управления в виде интегрирующего звена? Это облегчило бы пересчет параметров непрерывного регулятора в параметры цифрового по соотношениям (1ю123). Ответ должен быть однозначным: нет. Этому препятствуют следующие причины:
1) постоянная времени сервомотора, как правило, значительно меньше эквивалентной постоянной времени объекта, поэтому выходная величина реального объекта и с интегрирующей составляющей от сервомотора будут существенно отличаться;
2) система со статическим цифровым законом управления должна иметь статическую ошибку управления по возмущающему воздействию, действующему на объект, чего не будет в реальной системе;
3) такая система не позволяет реализовать ограничение на управляющее воздействие, что всегда имеет место в реальной системе и должно быть учтено при цифровом управлении, о чем говорилось ранее.
Таким образом, реализация цифрового закона управления должна проводиться по следующему алгоритму:
1) определить постоянную времени сервомотора;
2) определить минимальную длительность включения сервомотора, обеспечивающую 1% перемещение регулирующего органа;
3) отнеся сервомотор постоянной скорости к объекту управления и считая его идеальным интегрирующим звеним, произвести расчет оптимальных параметров непрерывного регулятора с желаемым законом управления;
4) найти период квантования цифрового регулятора, обеспечивающий отсутствие потери информации в системе управления;
5) дополнив математическую модель объекта управления дополнительным звеном чистого запаздывания равным двум периодам квантования, произвести пересчет оптимальных параметров регулятора и найти новый период квантования, который будет незначительно отличаться от предыдущего;
6) произвести пересчет параметров непрерывного регулятора в параметры цифрового.
Для проверки правильности проведенных расчетов целесообразно иметь имитационную модель цифровой системы, позволяющую построить переходный процесс с учетом ограничения на управляющее воздействие и скорость перемещения сервомотора. Практика расчетов показывает, что цифровой регулятор, учитывающий при реализации закона управления сервомотор постоянной скорости, обеспечивает устойчивую работу системы при наличии ограничения на управляющее воздействие а также на скорость перемещения сервомотора ( величину перемещения сервомотора за один период квантования, которая не должна превышать T/Tc).
2 Статистическая динамика
2.1 Основные задачи статистической динамики
Если структура и параметры системы управления остаются неизменными (фиксированными), а входное воздействие - заранее заданной функцией времени, то такая система называется детерминированной, а ее модель - детерминированной моделью.
В статистических (стохастических) моделях параметры и структура модели могут изменяться случайным образом, а входной сигнал является случайной функцией времени или случайной величиной.
Теория случайных процессов разработана советскими учеными Н.А. Колмогоровым, А.Я. Хинчиным, В.С. Пугачевым, В.В. Солодовниковым, а также зарубежными специалистами Н.Винером, К.Шенноном, Шерманом, Калманом и др. Впервые задача статистического синтеза была поставлена и решена на примере экстраполяции и интерполяции стационарных случайных последовательностей Н.А.Колмогоровым в 2940-2942 гг. Норберт Винер в 2945 г. распространил эту теорию на непрерывные случайные процессы и предложил решение задачи определения оптимальной системы с постоянными параметрами, находящейся под влиянием случайных стационарных воздействий.
В процессе работы системы автоматического управления - САУ на полезные сигналы накладываются помехи, являющиеся случайными функциями. Поэтому выходные координаты системы практически всегда представляют случайные функции времени. Достаточно общим статистическим критерием функционирования САУ является среднеквадратическая ошибка воспроизведения полезного сигнала СКО в условиях воздействия помех. Минимальное значение СКО соответствует оптимальным условиям функционирования САУ. Поэтому первой задачей статистической динамики является оценка СКО системы управления. Недостатком СКО в качестве критерия оптимизации работы САУ является то, что малое значение достигается лишь для средней, а не мгновенной ошибки. Поэтому в тех системах, не допускаются большие, хотя и кратковременные отклонения, желательно применение других методов.
Второй задачей статистического анализа является получение аналитических зависимостей, связывающих величину СКО с основными параметрами САУ. Это позволяет выбирать параметры системы такими, которые обеспечивают заданное или минимальное значение СКО. Если при заданной структуре САУ не удается получить требуемое качество управления, необходимо ее изменить с целью повышения фильтрующих свойств системы.
Третьей задачей статистического анализа является определение спектра флуктуаций выходной величины САУ, который зависит как от характеристик случайных воздействий, так и от параметров САУ. Эта задача играет важную роль при согласовании характеристик системы с последующими автоматическими устройствами.
Четвертой задачей статистического анализа является построение моделей на основе результатов наблюдений - идентификация в узком и широком смысле слова.
