- •Гоу впо Кубанский государственный технологический университет
- •Печатается по решению Редакционно-издательского совета КубГту
- •1 Цифровые системы управления
- •1.1 Способ управления с помощью эвм
- •1.2 Решетчатые функции и разностные уравнения
- •1.3 Условие устойчивости линейных импульсных систем, описанных разностными уравнениями
- •1.4 Дискретное преобразование Лапласа
- •1.5 Определение периода квантования при дискретном измерении без потери информации непрерывного сигнала
- •1.6 Основные свойства -преобразования
- •1.7 Дискретная передаточная функция
- •1.8 Получение оригинала из уравнений в конечных разностях и с помощью -преобразования
- •1.9 Цифровые аналоги типовых законов управления
- •1.10 Анализ цифровых систем управления
- •1.11 Анализ устойчивости цифровых систем.
- •1.12. Аналитический синтез алгоритма управления цифрового вычислительного устройства
- •1.13. Алгоритм цифрового управления по критерию быстродействия
- •1.14 Особенности реализации цифровых законов управления при использовании сервомоторов постоянной скорости
- •2.2 Характеристики случайных процессов
- •2.3 Стационарные случайные процессы
- •2.4 Основные свойства корреляционной функции и спектральной плотности стационарных случайных процессов
- •2.5 Прохождение случайных воздействий через линейную сау
- •2.6 Анализ систем регулирования при стационарных случайных воздействиях
- •2.7 Синтез сау при заданной структуре
- •2.8 Фильтр Винера - Колмогорова
1.12. Аналитический синтез алгоритма управления цифрового вычислительного устройства
В качестве критерия оптимизации при выборе параметров цифрового регулятора примем:
закончить переходный процесс на единичное ступенчатое воздействие за определенное время, переходный процесс должен быть апериодическим.
В основу метода положено представление процесса на выходе системы степенным рядом. Рассмотрим структурную схему системы с цифровым регулятором.
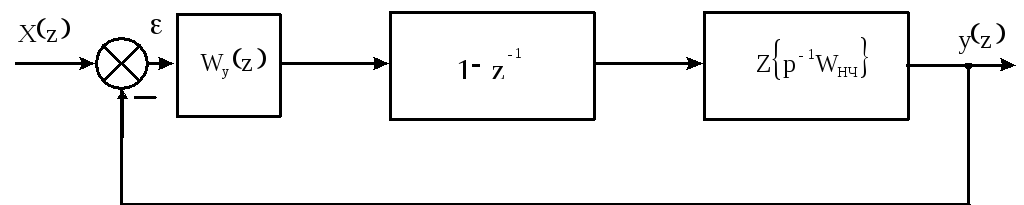
Рисунок 1.9 - Структурная схема системы с цифровым регулятором
Найдем передаточную функцию замкнутой системы между заданным значением X(Z) и ошибки управления (Z).
|
|
(1.76) |
где
|
|
(1.77) |
Решетчатая функция ошибки может быть найдена так:
|
|
(1.78) |
Примем первый
порядок астатизма системы, поскольку
система предназначается для стабилизации
регулируемой величины, и, следовательно,
будет обладать нулевой статической
ошибкой регулирования. В этом случае
передаточная функция замкнутой системы
![]() должна делится на
должна делится на
![]() и, следовательно, ее можно представить
так:
и, следовательно, ее можно представить
так:
|
|
(1.79) |
Из выражений (1.78) и
(1.79) следует, что изображение ошибки
системы, имеющей астатизм первого
порядка, при обработке единичного
сигнала равно
![]() , которое можно представить суммой
бесконечного ряда:
, которое можно представить суммой
бесконечного ряда:
|
|
(1.80) |
В этом выражении
![]() при
при
![]() .
Кроме того,
.
Кроме того,
![]() ,
когда
,
когда
![]() .
Здесь
.
Здесь
![]() - безразмерное (относительное) время
переходного процесса.
- безразмерное (относительное) время
переходного процесса.
Передаточная функция замкнутой системы между заданным и действительным значением регулируемой величины:
|
|
(1.81) |
Из выражения (1.81) можно записать алгоритм цифрового вычислительного устройства
![]() или
или
|
|
(1.82) |
Таким образом,
задача синтеза алгоритма цифрового
управления сводится к определению
![]() ,
или для астатической системы
,
или для астатической системы
![]() .При
этом необходимо удовлетворить следующие
требования:
.При
этом необходимо удовлетворить следующие
требования:
1. Алгоритм ЦВУ должен
быть физически реализуем. Это условие
заключается в сравнении степени полинома
числителя и знаменателя
![]() относительно переменной
относительно переменной
![]() .
При этом
.
При этом
![]() определяется по выражению (1.82).
определяется по выражению (1.82).
2. Замкнутая система должна быть устойчива.
3. Передаточная
функция
![]() должна быть полиномом минимальной
степени
должна быть полиномом минимальной
степени
![]() .
.
Поскольку непрерывная
часть цифровой системы управления (ЦСУ)
инерционная и, следовательно, переходная
функция
![]() непрерывна и
непрерывна и
![]() ,
то
,
то
![]() будет делиться на
будет делиться на
![]() .
.
|
|
(1.83) |
где
![]() .
.
Степень полинома
![]() на единицу (или более) меньше степени
полинома
на единицу (или более) меньше степени
полинома
![]() .
.
Пусть ряд,
образовавшийся из передаточной функции
![]() имеет вид:
имеет вид:
|
|
(1.84) |
Используя выражение (1.82), передаточную функцию цифрового устройства можно записать так:
|
|
(1.85) |
Если
![]() ,
то степень полинома числителя
,
то степень полинома числителя
![]() на единицу больше степени полинома
знаменателя, т.е. алгоритм ЦВУ не
реализуем. Следовательно, условие
реализуемости алгоритма
на единицу больше степени полинома
знаменателя, т.е. алгоритм ЦВУ не
реализуем. Следовательно, условие
реализуемости алгоритма
![]() заключается в том, чтобы
заключается в том, чтобы
![]() делилась на
делилась на
![]() (или на
(или на
![]() ,
где
,
где
![]() - индекс передаточной функции линейной
части - разница степеней полиномов
знаменателя и числителя относительно
- индекс передаточной функции линейной
части - разница степеней полиномов
знаменателя и числителя относительно
![]() ).
Таким образом, должно выполняться
условие:
).
Таким образом, должно выполняться
условие:
|
|
(1.86) |
Из требования устойчивости вытекают следующие особенности формирования закона цифрового управления:
1. Так как
![]() ,
то устойчивость замкнутой САУ определяется
наличием полюсов или нулей передаточной
функции
,
то устойчивость замкнутой САУ определяется
наличием полюсов или нулей передаточной
функции
![]() на окружности единичного радиуса или
вне ее.
на окружности единичного радиуса или
вне ее.
2. Полюс
![]() во внимание не принимается.
во внимание не принимается.
Если полюс
![]() на окружности или вне ее и этот полюс
на окружности или вне ее и этот полюс
![]() .
Передаточные функции
.
Передаточные функции
![]() представляются полиномами относительно
представляются полиномами относительно
![]() вида (1.83), поэтому
вида (1.83), поэтому
![]() ,
если одна из функций
,
если одна из функций
![]() или
или
![]() имеет нуль равный
имеет нуль равный
![]() .
Но так как
.
Но так как
![]() есть степенной ряд, то пусть
есть степенной ряд, то пусть
![]() .
В этом случае неустойчивый полюс
устраняется неустойчивым нулем алгоритма
ЦВУ. Поскольку ЦВМ работает неточно
из-за ошибки квантования, то это приводит
к смещению полюсов и нулей
.
В этом случае неустойчивый полюс
устраняется неустойчивым нулем алгоритма
ЦВУ. Поскольку ЦВМ работает неточно
из-за ошибки квантования, то это приводит
к смещению полюсов и нулей
![]() и, следовательно, к неустойчивости всей
системы. Отсюда вывод:
и, следовательно, к неустойчивости всей
системы. Отсюда вывод:
неустойчивые
полюса передаточной функции
![]() должны быть нулями передаточной функции
должны быть нулями передаточной функции
![]() .
.
Если
![]() - нуль передаточной функции
- нуль передаточной функции
![]() ,
то передаточная функция
,
то передаточная функция
![]() должна иметь полюс, равный
должна иметь полюс, равный
![]() ,
или передаточная функция
,
или передаточная функция
![]() должна иметь ноль, равный
должна иметь ноль, равный
![]() ,
т.е.
,
т.е.
![]()
Поскольку все полюса
![]() совпадает с началом координат, то
компенсировать нуль, равный
совпадает с началом координат, то
компенсировать нуль, равный
![]() ,
она не может.
,
она не может.
Пример. Произвести синтез алгоритма ЦВМ, обеспечивающего переходный процесс без перерегулирования и заканчивающимся за минимальное время.
Дано

Решение
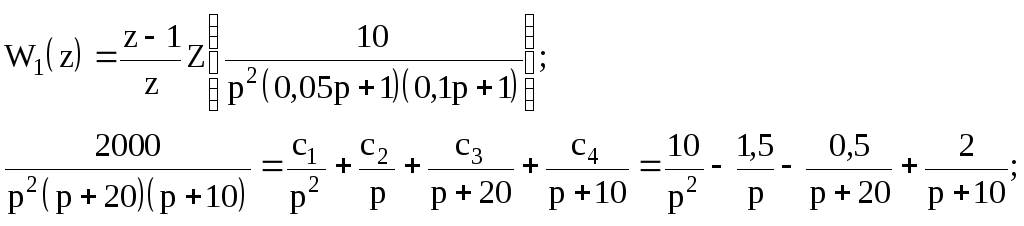
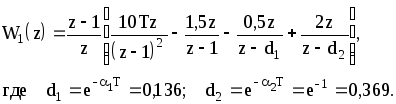
С учетом
![]() после несложных преобразований получаем
после несложных преобразований получаем
![]() .
.
Числитель можно записать в виде:
![]()
где
 .
.
Теперь можно найти
передаточную функцию замкнутой системы
Ф(z).
Она должна делиться на
![]() (условие физической реализуемости
алгоритма ЦВМ) и на
(условие физической реализуемости
алгоритма ЦВМ) и на
![]() (условие устойчивости).
(условие устойчивости).
Поэтому примем:
|
|
(1.87) |
где
![]() - неопределенный множитель. Из выражения
(1.87) видно, что Ф(z)
- полином минимальной степени,
удовлетворяющий приведенным выше
требованиям.
- неопределенный множитель. Из выражения
(1.87) видно, что Ф(z)
- полином минимальной степени,
удовлетворяющий приведенным выше
требованиям.
Так как
![]() обладает астатизма первого порядка, то
передаточная функция ошибки должна
делиться на
обладает астатизма первого порядка, то
передаточная функция ошибки должна
делиться на
![]() Кроме того, из (1.87) следует что
Кроме того, из (1.87) следует что
![]() - полином второй степени относительно
- полином второй степени относительно
![]() ,
следовательно,
,
следовательно,
|
|
|
где
![]() - величины, подлежащие определению.
- величины, подлежащие определению.
Подставив значение
![]() в выражение (1.87), получим:
в выражение (1.87), получим:
|
|
из которого следует
![]()
С учетом полученного результата
|
|
Алгоритм ЦВМ,
определяемый поставленными требованиями
с учетом
![]() ,
имеет вид:
,
имеет вид:
|
|
Ошибка системы при
отработке единичной ступенчатой функции
![]() при
при
![]() имеет вид:
имеет вид:
![]()
откуда числовая последовательность
![]()
т.е. ошибка обращается
в нуль, начиная с момента
![]() ,
поэтому время регулирования равно
,
поэтому время регулирования равно
![]() ,
переходный процесс монотонный.
,
переходный процесс монотонный.

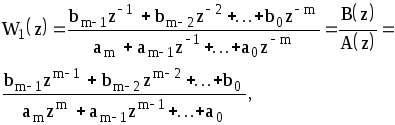
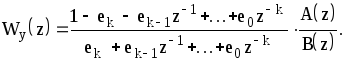
 (1.88)
(1.88)