8. Осевая деформация

Осевая деформация стержня возникает в случае, когда вся внешняя нагрузка сводится к силам, действующим по оси стержня. Из шести внутренних усилий отлична от нуля только продольная сила . Для определения продольной силы используется метод сечений. Продольная сила связана с нормальным напряжением условием статической эквивалентности

(2.9)

Согласно гипотезе Бернулли при осевой деформации . Из формулы (2.7), выражающей закон Гука для линейной деформации, следует . Условие статической эквивалентности (2.9) с учетом приводится к виду

(2.10)

Для каждого материала существует некоторый предельный уровень нормального напряжения (- опасное напряжение), при достижении которого в материале возникают необратимые деформации (пластичный материал) или начинается разрушение (хрупкий материал).

Эти опасные уровни нормального напряжения обозначаются (предел текучести) и (предел прочности). Величины напряжений и определяются опытным путем (методика испытаний подробно рассмотре­на в лабораторных работах №№ 1,2).

В расчетах по методу допускаемых напряжений условие прочности материала записывается в виде

, (2.11)

где k - коэффициент запаса по прочности, k>1;

- допускаемое нормальное напряжение

Условие прочности при растяжении – сжатии:

(2.12)

В стержнях постоянного поперечного сечения наибольшие напряжения возникают в сечении, в котором действует наибольшая (независимо от знака) продольная сила, - опасное сечение. Для определения положения опасного сечения строится график (эпюра) изменения продольной силы по длине стержня.

Три типа задач, вытекающие из условия прочности (2.12):

• проверка прочности ;

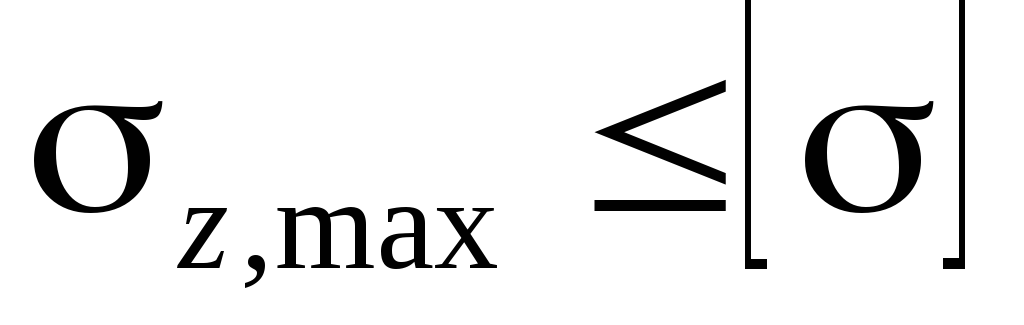• подбор поперечного сечения ;

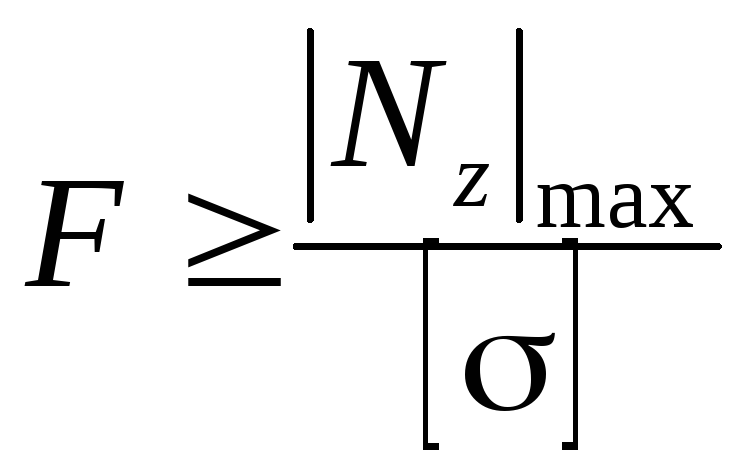• определение несущей способности .

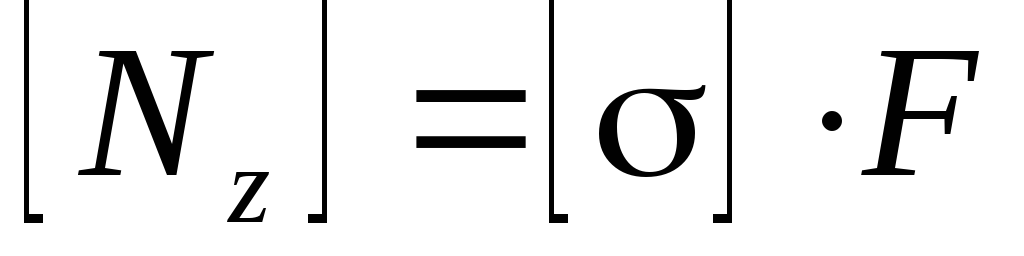Для вычисления удлинений при осевой деформации составляется интеграл вида

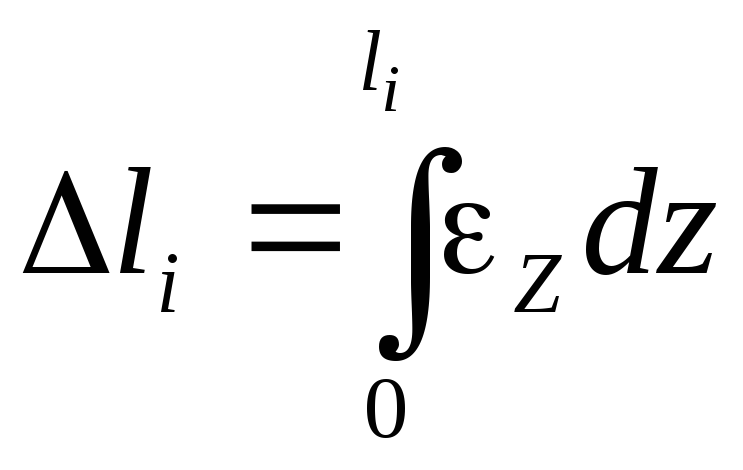(2.13)

Подстановка под интеграл из формулы (2.7) и из формулы (2.10) дает

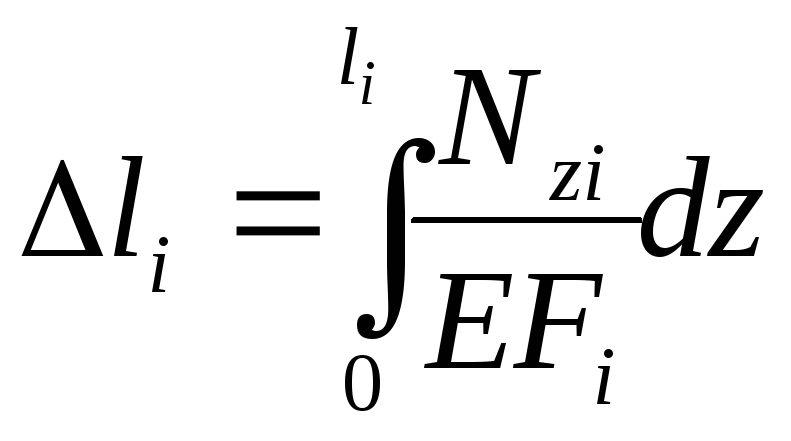(2.14)

На практике часто продольная жесткость является величиной постоянной .

Вынося за знак интеграла постоянную , формулу (2.14) можно переписать в виде

, (2.15)

где - площадь эпюры продольной силы (с учетом знака) на участке стержня длины . Если дополнительно принять и , то формула (2.14) принимает вид

(2.16)

1. Статически неопределимые задачи при осевом действии сил

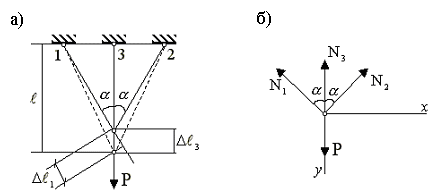
На рис.2.6.а показана статически неопределимая шарнирно–стержневая система.

Для определения усилий в элементах системы вырезается узел с силой Р (рис.2.6.б) и составляются уравнения равновесия сил, действующих в узле:

, , (2.17)

,

(2.18)

Два уравнения равновесия (2.17) и (2.18) содержат три неизвестных усилия , - данная система один раз статически неопределимая.

Для решения задачи составляется уравнение, которое связывает деформации отдельных элементов системы (уравнение совместности деформаций). Под действием силы Р узел системы переместится вертикально вниз (на рис.2.6.а пунктирной линией показаны положения элементов после деформации системы). Из рассмотрения картины деформации следует

(2.19)

Рис.2.6

Уравнение совместности деформаций (2.19) с помощью закона Гука для осевой деформации переписывается в усилиях

(2.20)

Принимается , .

Учитывая, что и , формула (2.20) принимает вид

(2.21)

Уравнения (2.17), (2.18), (2.21) образуют систему, достаточную для решения задачи. После элементарных преобразований в ответе получается:

, (2.22)