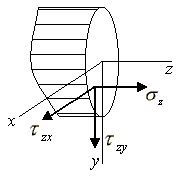
4. Внутренние усилия в поперечном сечении стержня

Составим шесть уравнений равновесия для левой отсеченной части:

; ;

;

; ;

.

Интегралы в этих выражениях имеют специальные обозначения и названия:

 ‑ продольная сила; (2.1)

 ‑ поперечная сила; (2.2)

 ‑ поперечная сила; (2.3)

 ‑ изгибающийся момент (относительно оси x); (2.4)

 ‑ изгибающийся момент (относительно оси y); (2.5)

 ‑ крутящий момент (относительно продольной оси) (2.6)

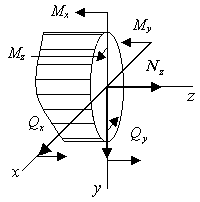
Введенные шесть функций определяют шесть внутренних усилий, которые действуют в поперечных сечениях прямоосного призматического стержня (рис.2.3.б).

а)	б)
Рис.2.3.

5. Деформации

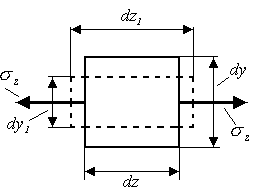
Нормальные напряжения вызывают изменение линейных размеров (длин) элементарных отрезков. Линейные отрезки увеличиваются в длине (); линейные отрезки и уменьшаются в длине () (рис.2.4.а). Мерой изменения линейных размеров в окрестности точки является относительная линейная деформация , которая определяется по формуле:

.

Деформации определяются аналогично.

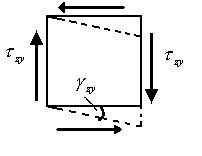
Касательные напряжения вызывают искажение формы элементарного параллелепипеда (рис.2.4.б), - деформация сдвига.

а)	б)
Рис.2.4

6. Закон Гука

Связь напряжений с деформациями устанавливается опытным путем (см. лабораторные работы ). Аппарат сопротивления материалов базируется на линейной связи напряжений и деформаций:

, (2.7) где - модуль продольной упругости (модуль Юнга);

, (2.8) где - модуль сдвига.

Приведенные формулы выражают Закон Гука для линейной деформации и деформации сдвига.

7. Гипотеза плоских сечений

Гипотеза плоских сечений (гипотеза Бернулли) составляет основу аппарата сопротивления материалов. Ее суть заключена в следующем положении: при простейших видах деформации стержня любое поперечное сечение остается плоским и перпендикулярным к оси стержня.

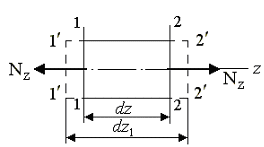
При осевом растяжении или сжатии поперечные сечения перемещаются поступательно вдоль оси z стержня (рис.2.5.а). Все элементарные отрезки dz (параллельные оси z) после деформации получают одинаковое приращение длины, равное . Следовательно, относительная линейная деформация этих отрезков является величиной постоянной.

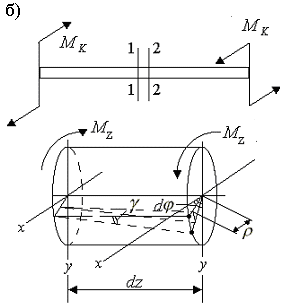
При чистом кручении поперечные сечения поворачиваются относительно оси z стержня (рис.2.5.б). Из картины деформации элементарной части стержня следует соотношение , или ( - удаленность слоя материала от оси z стержня).

Рис.2.5

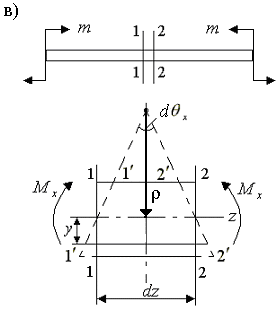
При чистом изгибе поперечные сечения поворачиваются относительно оси x (рис.2.5.в). Элементарный отрезок , удаленный от оси стержня на величину y, получает приращение длины равное . Относительная линейная деформация определяется выражением . Представляя как , получаем (где - радиус кривизны нейтрального слоя).