5. Задача 5 "Плоский поперечный изгиб стержня".

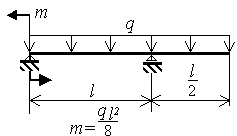
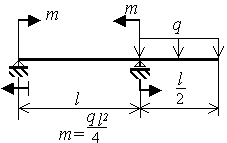
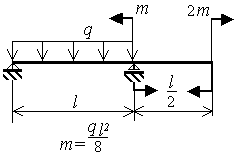
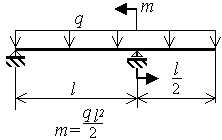
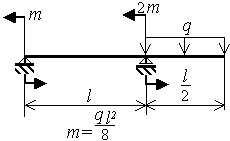
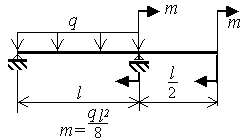
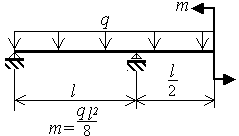
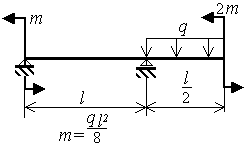
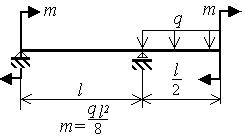
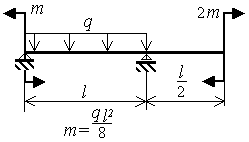
Шарнирно опертая однопролетная балка с консолью нагружена равномерно распределенной нагрузкой q и моментами m (рис.3.9)

Требуется:

1. Вычертить в масштабе схему балки и указать числовые значения размеров и нагрузок.

2. Построить эпюры изгибающего момента М_x и поперечной силы Q_y (эпюры М_x и Q_y расположить обязательно под схемой балки).

3. Подобрать поперечное сечение балки в виде двутавра.

4. Проверить прочность балки в точках, расположенных на нейтральной оси.

Исходные данные приведены в таблице 5 и на рис.3.9.

Рис.3.9

Таблица 5

Номер схемы (рис.5)	1	2	3	4	5	6	7	8	9	0	А
, м	4	5	6	7	4	5	6	7	4	6	В
q кН/м	10	12	14	16	18	20	10	12	14	16	А

Принять

Пример решения задачи.

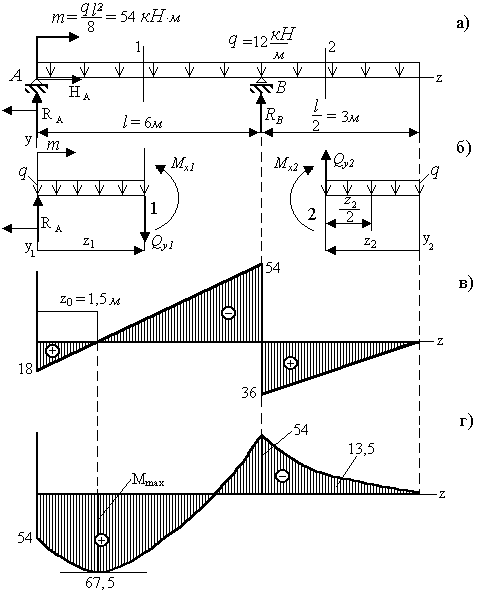
Схема балки приведена на рис.3.10.а.

1. Построение эпюр внутренних усилий в балке.

Для определения реакций опор составляются уравнения равновесия:

(точка А совпадает с шарниром левой опоры)

(3.11)

(точка В совпадает с шарниром правой опоры)

(3.12)

(3.13)

Из уравнения (3.11) определяется реакция R_В

или .

Из уравнения (3.12) определяется реакция R_А

или

Проверка: ;

или .

Рис. 3.10

Для определения внутренних усилий в пролете балки проводится сечение 1 (рис.3.10.б). В сечении 1 показываются положительные внутренние усилия и М_х1.

Длина отсеченной части ‑ переменная величина .

Для отсеченной части составляются два уравнения равновесия

;

или (3.14)

;

(3.15)

Переменная z₁ может принимать любое значение в пределах пролета балки, то есть .

Для определения усилий, действующих в поперечных сечениях консольной части балки проводится сечение 2 (Рис.3.10.б). Длина отсеченной части ‑ переменная величина z₂. В сечении 2 показываются положительные внутренние усилия , М_х2.

Для отсеченной части составляется два уравнения равновесия

; или (3.16)

, или (3.17)

Диапазон изменения переменной z₂: .

По полученным выражениям для , М_х строятся эпюры усилий.

Поперечная сила изменяется по длине балки по линейному закону и . Для построения графика линейной функции вычисляются значения функции в двух точках, ‑ в начале и в конце каждого участка.

, , , ,

, ,

Для построения эпюры поперечной силы проводится ось z (рис.3.10.в). Выбирается масштаб эпюры (произвольно) и в начале и конце каждого участка балки откладываются вычисленные значения . В сопротивлении материалов принято характерные ординаты эпюр сопровождать числовыми значениями и указывать знаки усилий.

Эпюра изгибающего момента М_х строится аналогично: проводится ось z; выбирается масштаб эпюры М_х (масштаб эпюры М_х не связан с масштабом эпюры ); в начале и конце каждого участка откладываются ординаты, равные вычисленным значениям изгибающего момента (рис.3.10.г).

В данном примере функция изгибающего момента М_х описывается параболой второй степени. Парабола второй степени строится по трем точкам: две точки граничные (начало и конец участка), а третья точка – точка экстремума функции. Условие экстремума функции М_х

(3.18)

Из теории изгиба известно, что условие (3.18) означает равенство нулю поперечной силы . На эпюре видно, что функция М_х имеет экстремум в пролете балки (нулевое значение ординаты функции ). Для определения координаты следует функцию приравнять к нулю. Согласно выражению (3.14)

или

Для вычисления экстремального значения изгибающего момента М_х в выражение (3.15) подставляется

или

В пределах консоли сечение с нулевым значением поперечной силы совпало с граничным сечением. Это означает, что функция изгибающего момента М_х достигает экстремального значения на правом краю консоли. В этом случае третья точка, необходимая для построения эпюры изгибающего момента М_х принимается в середине консоли, т.е. , или

Основное назначение эпюр и М_х заключается в определении опасных сечений в балке. Сечение с наибольшим значением изгибающего момента (независимо от знака) определяет первое опасное сечение, в котором действуют наибольшие нормальные напряжения :

(3.19)

Проверка прочности балки по нормальным напряжениям заключается в выполнении условия

(3.20)

Сечение с наибольшим значением поперечной силы (независимо от знака) определяет второе опасное сечение, в котором действуют наибольшие касательные напряжения , которые вычисляются по формуле Журавского:

(3.21)

Проверка прочности балки по касательным напряжениям выполняется по формуле

,

2. Подбор поперечного сечения балки

Подбор поперечного сечения балки производится по формуле:

(3.22)

Здесь и

- требуемый момент сопротивления поперечного сечения балки. Для подбора сечения балки в виде двутавра используются специальные таблицы, которые называются сортамент (см. приложение). В сортаменте «Балки двутавровые» в столбце находится число, ближайшие к искомому . Такими ближайшими числами являются и . Выбирается большее значение . Это число определяет строку в таблице, а левое крайнее число в строке определяет номер прокатного профиля, - двутавр №30.

3. Проверка прочности балки в точках, расположенных на нейтральной оси.

В точках, расположенных на нейтральной оси, касательные напряжения достигают максимальных значений:

Значения величин , , выписываются из сортамента для заданного номера двутавра. , , .

Примечание. В формуле Журавского величина означает ширину сечения в месте вычисления напряжений. В сортаменте этот размер обозначен , то есть . Подстановка числовых данных дает

.

Вывод:

1. Подобрано сечение балки в виде двутавра №30.

2. Прочность балки по касательным напряжениям обеспечивается