
- •К санкт-петербург 2004 афедра "Прочность материалов и конструкций"
- •Введение
- •Программа курса
- •Основные понятия
- •Осевое растяжение и сжатие прямоосного стержня
- •Механические свойства материалов
- •Основы теории напряженного и деформированного состояний в локальной области деформированного твердого тела
- •Классические теории прочности и пластичности
- •Геометрические характеристики поперечных сечений стержней
- •Кручение прямоосного стержня
- •Изгиб прямоосного стержня
- •Идеализации, применяемые в сопротивлении материалов.
- •Внешние силы.
- •Механическое напряжение
- •Внутренние усилия в поперечном сечении стержня
- •Деформации
- •Закон Гука
- •Гипотеза плоских сечений
- •Осевая деформация
- •Статически неопределимые задачи при осевом действии сил
- •Понятие о методе расчета по разрушающим (допускаемым) нагрузкам.
- •Кручение.
- •Подстановка формулы (2.24) в условие эквивалентности (2.23) дает
- •Поперечный изгиб.
- •Правило знаков для и .
- •Чистый изгиб.
- •Наибольшие нормальные напряжения в сечении стержня возникают в точках наиболее удаленных от нейтральной оси х, то есть
- •Задания на контрольные работы с примерами решения.
- •Задача 1 "Расчет прямоосного ступенчатого стержня на осевое действие сил".
- •Пример решения задачи.
- •Рассматривается равновесие нижней отсеченной части (рис3.2.Г)
- •Задача 2 "Расчет статически определимой шарнирно-стержневой системы".
- •Пример решения задачи.
- •Определение продольных сил в стержнях системы.
- •Задача 3 "Расчет статически неопределимой шарнирно-стержневой системы"
- •Пример выполнения задачи1
- •Определение грузоподъемности системы по методу допускаемых напряжений.
- •Задача 4 "Кручение прямоосного составного стержня".
- •Пример решения задачи.
- •Задача 5 "Плоский поперечный изгиб стержня".
- •Пример решения задачи.
- •Лабораторный практикум
- •Лабораторная работа № 1. "Растяжение стального образца до разрыва".
- •Для проведения испытаний используется разрывная машина, снабженная записывающим устройством. В процессе испытания автоматически вычерчивается диаграмма растяжения.(рис.4.2)
- •Определение удельной работы разрыва.
- •Лабораторная работа № 2. "Испытание на сжатие образцов из различных материалов"
- •Лабораторная работа № 3. "Исследования упругих свойств стали при растяжении – сжатии".
- •Лабораторная работа № 4. "Исследование упругих свойств стали при кручении".
- •Контрольные вопросы к защите лабораторных работ
- •Контрольные вопросы к зачету и экзамену1
- •Часть 1
- •Приложение
Пример выполнения задачи1
Абсолютно жесткий
диск опирается на шарнирно - неподвижную
опору и поддерживается двумя стальными
стержнями (рис.3.6.а). Исходные данные:
![]() .
.
-
Определение усилий в стержнях системы.
На
рис. 3.6.б показана система сил, действующих
на абсолютно жесткий диск (продольные
силы
![]() ,
,
![]() показаны положительными).
показаны положительными).
Уравнение равновесия:
![]() Рb-
Рb-![]() (a+b)-
(a+b)-
![]() с=0
2,6
NZ1+1,6
с=0
2,6
NZ1+1,6
![]() =1,4Р
(3.3)
=1,4Р
(3.3)
![]() Н0=0
(3.4)
Н0=0
(3.4)
![]() -Р+
-Р+
![]() -R0
-
-R0
-![]() =0
=0
![]() -
-![]() –
R0=P
(3.5)
–
R0=P
(3.5)
Два
уравнения равновесия (3.3) и (3.5) содержат
три неизвестные
![]() ,
,
![]() ,
R0 – данная
система статически неопределимая.
,
R0 – данная
система статически неопределимая.
Статически неопределимыми называются задачи, которые не могут быть решены с помощью одних уравнений статики (равновесия). Для решения таких задач дополнительно составляются уравнения, в которые входят абсолютные деформации стержней системы. Такие уравнения называются уравнениями совместности деформаций. Для составления этих уравнений используется картина деформации системы.
|
|
|
Рис.3.6 |
в) Рис.
3.6
Под
действием силы Р абсолютно жесткий
диск, сохраняя прямолинейную форму,
поворачивается относительно шарнира
опоры (показано на рис.3.6.а пунктирной
линией). Шарниры А и В переместятся в
новые положения А1 и В1. Длина
отрезка АА1 определяет абсолютную
деформацию первого стержня, т.е.
![]() =
=![]() l1;
аналогично
l1;
аналогично
![]() =
=![]() l2.
Из подобия треугольников ОАА1 и
ОВВ1 составляется пропорция:
l2.
Из подобия треугольников ОАА1 и
ОВВ1 составляется пропорция:
![]() (3.6)
(3.6)
Соотношение (3.6) и есть уравнение совместности деформаций.
Примечание. В данной задаче
величины
![]() l1
и
l1
и
![]() l2
положительные (стержни 1 и 2 удлиняются).
Если стержень на картине деформации
укорачивается (
l2
положительные (стержни 1 и 2 удлиняются).
Если стержень на картине деформации
укорачивается (![]() l
< 0), то в уравнении совместности
деформаций абсолютная деформация
записывается со знаком минус.
l
< 0), то в уравнении совместности
деформаций абсолютная деформация
записывается со знаком минус.
Уравнение совместности деформаций с помощью закона Гука переписывается в усилиях и вместе с уравнением равновесия (3.3) образует систему уравнений, достаточную для определения всех неизвестных задачи.
![]() или
или
![]() (3.7)
(3.7)
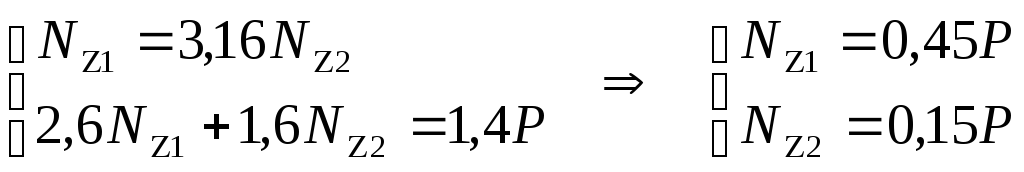 (3.8)
(3.8)
-
Определение грузоподъемности системы по методу допускаемых напряжений.
Грузоподъемность
![]() системы определяется как часть от
опасной
системы определяется как часть от
опасной
![]() нагрузки:
нагрузки:
![]() ,
где k – коэффициент
запаса по прочности.
,
где k – коэффициент
запаса по прочности.
При расчете по методу допускаемых напряжений за опасное состояние системы принимается такое, при котором хотя бы в одном элементе возникает пластическая деформация. Такой элемент называется опасным. Для определения опасного элемента вычисляется напряжение в каждом стержне системы.
Стержень 1:
![]()
Стержень 2:
![]()
Так как
![]() ,
то опасный элемент системы – стержень
1. Из условия
,
то опасный элемент системы – стержень
1. Из условия
![]() (
(![]() - предел текучести) определяется величина
опасной нагрузки
- предел текучести) определяется величина
опасной нагрузки
![]() Н=533,3 кН.
Н=533,3 кН.
Допускаемое
значение нагрузки
![]() при расчете по методу допускаемых
напряжений:
при расчете по методу допускаемых
напряжений:
![]() кН,
(3.9)
кН,
(3.9)
где k – коэффициент запаса по прочности принят равным 1,5.
-
Определение грузоподъемности по методу разрушающих (допускаемых) нагрузок.
Согласно метода расчета по разрушающим (допускаемым) нагрузкам за опасное состояние системы принимается такое, которое соответствует полному исчерпанию несущей способности.
Развитие пластической
деформации в стержне 1 сдерживается
упруго работающим материалом стержня
2.При возникновении пластической
деформации во втором стержне вся система
переходит в состояние пластического
течения. И если принять для материала
стержней диаграмму идеально
упругопластического материала (диаграмма
Прандтля)
![]() ,
то возникновение пластической деформации
во втором стержне соответствует
исчерпанию несущей способности системы
(система становится механизмом).
,
то возникновение пластической деформации
во втором стержне соответствует
исчерпанию несущей способности системы
(система становится механизмом).
Разрушающая нагрузка определяется из уравнения равновесия, составленного для системы, находящейся в предельном состоянии (рис.3.6,в).
![]()
![]() (3.10)
(3.10)
![]() Н = 610 кН
Н = 610 кН
Допускаемая нагрузка
![]() по
методу разрушающих (допускаемых) нагрузок
по
методу разрушающих (допускаемых) нагрузок
![]() кН
кН
Таким образом, метод расчета по допускаемым (разрушающим) нагрузкам выявляет резерв прочности конструкции.

