2.4. Потоки восстановления
Пусть на временной оси некоторый момент времени выбран за 0 и пусть t1, t2, t3,…> 0 – моменты наступления событий (см. рис. 1)
0
Рис. 1 Поток событий
Обозначим τ1 = t1, τn = tn – tn-1 – длины интервалов между моментами наступления событий. Отметим принципиальное отличие τ1 от всех остальных τn: если τn , n ≥ 2 отсчитываются от момента наступления предыдущего события потока, то τ1 отсчитывается от нуля на оси времени, никакого отношения к потоку не имеющего.
Случайный
поток называется потоком с ограниченным
последействием,
если
– независимые случайные величины.
Смысл слов «ограниченное последействие» следующий: будущее поведение потока после момента времени t, tn < t < tn+1, зависит лишь от конечной величины (t – tn), а от остального прошлого не зависит.
Для описания потока с ограниченным последействием достаточно задать функции распределения Ak (x) = P{ τk < x}, k ≥ 1.
Поток с ограниченным последействием, для которого Ak (x) = A(x) для k ≥ 2 (заметьте: A1 (x) это не касается) называется процессом восстановления. В последнем случае вместо слов «наступило событие потока», часто говорят «наступило восстановление».
Пусть Nt – число событий, наступивших на интервале (0,t). Функция H(t) = M{Nt} называется функцией восстановления. Функция h(t) = H´(t), если она существует, называется плотностью восстановления. По смыслу h(t)dt (или dH(t)) есть вероятность того, что на интервале [t, t + dt] наступит событие потока. (интенсивность равна параметру потока)
Выведем теперь одно из основных уравнений – уравнение для H(t). Имеем
P{Nt = n} = P{tn < t, tn+1 ≥ t}.
Но, с другой стороны
P{tn < t} = P{tn+1 < t} + P{tn < t, tn+1 > t },
откуда
P{tn < t, tn+1 > t } = P{tn < t} – P{tn+1 < t}.
Поэтому для H(t) = M{Nt} имеем
.
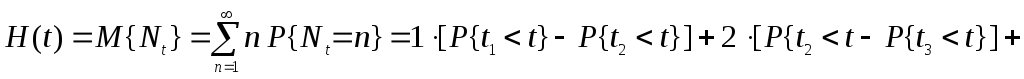
Так как tn = τ1 + τ2 + τ3 …+ τn, то
P{t1 < t} = F1 (t) = A1 (t),
,
,
……………………………………………………..
.
Поэтому
.
Итак, функция восстановления удовлетворяет интегральному уравнению
.
(16)
Решить его можно через преобразования Лапласа-Стилтьеса. Действительно, применяя это преобразование к обеим частям уравнения, получим
,
откуда
.
(17)
Зная
A*(s)
и
,
отсюда находится H*(s),
а по таблицам обратного преобразования
Лапласа-Стилтьеса и H(t).
Пример
Пусть A(x) = 1 – e-λx, A1(x) = 1 – e-µx. Тогда
,
.
Поэтому
,
и отсюда
.
Рассмотрим теперь некоторые следствия из уравнения (16) и его решения (17)
1.
Пусть
и λ = 1/a.
Заметим, что A*(0)
= A(∞)
– A(0)
= 1.
Тогда
,
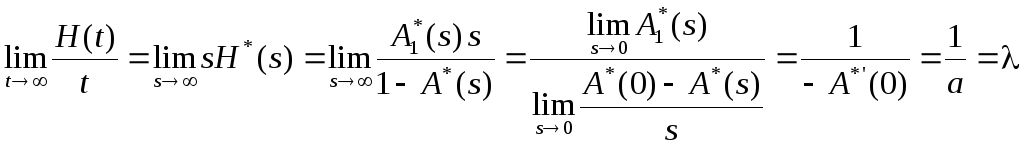то
есть при t
→∞
ведет себя как λt.
2. Пусть Q(t) – неотрицательная интегрируемая на (0,∞) функция. Тогда по свойствам преобразования Лапласа-Стилтьеса
.
По свойствам преобразования Лапласа-Стилтьеса
Окончательно
,
. (18)
Эта формула называется основной теоремой теории восстановления.
2.5. Распределение величины перескока и недоскока для потоков восстановления
Рассмотрим некоторый произвольный момент времени t в потоке восстановления, который окружают моменты tn и tn+1 наступления событий потока. Величина tn+1 – t = γ(t) называется временем (или величиной) перескока, а величина γ* = t – tn – величиной недоскока (см. рис. 2).
0
t
Рис.2. Перескок и недоскок
Для процесса γ(t), характеризующего величину перескока, обозначим
P(γ(t) < x) = F(t ,x),
тогда
F(t + Δt, x) = F(t, x + Δt) – F(t, Δt) + F(t, Δt)A(x) + ο(Δt).
Разложим функцию F по приращению аргументов в ряд Тейлора с точностью до ο(Δt):
.
Уничтожая F(t, x) в обеих частях и сокращая на Δt, получим
.
В
стационарном режиме
,
тогда
,
следовательно
,
полагая x → ∞, получим
,
откуда
F´(0) =1/a = λ.
Таким образом, функция распределения F(x) величины перескока имеет вид
.
Для процесса γ*(t), характеризующего величину недоскока, обозначим
P(γ*(t) < x) = G(t, x),
P(x ≤ γ*(t) < x + dx) = g(t, x)dx,
тогда
,
и следовательно
.
В стационарном режиме g(t, x) ≡ g(x), поэтому g(x) удовлетворяет уравнению
,
решение которого имеет вид
g(x) = C(1 – A(x)).
Интегрируя
это равенство по
в интервале
,
получим
,
откуда следует, что
C =1/a = λ.
Таким образом
g(x) = λ(1 – A(x)),
а для функции распределения G(x) величины недоскока можно записать
.