1.6. Процесс размножения и гибели

Процессом размножения и гибели называется однородная цепь Маркова с непрерывным временем, принимающая значение i=0,1,2,…, для которой за время Δt возможны переходы из состояния i лишь в соседние состояния: i – 1 и i + 1, то есть для инфинитезимальных характеристик которой выполнены следующие условия

,

.

Такие процессы достаточно адекватны многим реальным процессам в биологии, физике, социологии, демографии, экономике, теории массового обслуживания.

Для удобства обозначим

q_ii-1 = µ_i , q_ii+1 = λ_i,

тогда можно записать

p_ii+1(Δt) = λ_iΔt + o(Δt), p_ii-1(Δt) = µ_iΔt + o(Δt),

p_ii(Δt) =1 – (λ_i + µ_i)Δt + o(Δt).

Если значение процесса интерпретировать как число заявок в некоторой системе массового обслуживания, то λ_iΔt + o(Δt) есть вероятность поступления новой заявки в систему с i заявками, а µ_iΔt + o(Δt) – вероятность окончания обслуживания заявки и её ухода из системы за время Δt.

Прямая и обратная системы дифференциальных уравнений Колмогорова для процесса гибели и размножения имеют вид

, (15)

. (16)

Найдём стационарное распределение вероятностей значений процесса гибели и размножения.

Система уравнений Колмогорова для стационарных вероятностей π_j в этом случае примет вид

π_j-1λ_j-1 – π_j(λ_j + µ_j) + π_j+1µ_j+1 = 0, j=1,2,…, (17)

-π₀λ₀ + π₁µ₁ = 0, (18)

. (19)

1.7. Метод Хинчина

Применяя метод Хинчина, обозначим

z_j = π_j-1λ_j-1 – π_jµ_j,

тогда из (18) получим z₁ = 0, а из (17) запишем равенства z_j = z_j+1, следовательно, имеет место равенство π_j-1λ_j-1 – π_jµ_j = 0, откуда получим равенство

.

Вероятность π₀ найдём из условия нормировки (19)

,

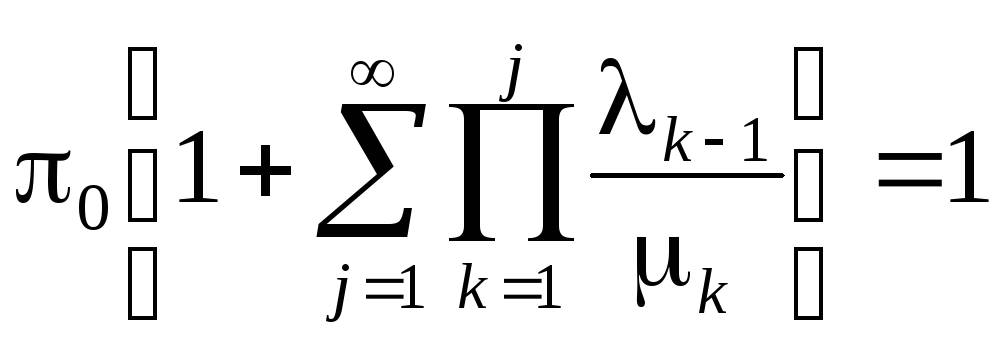откуда получим

.

Здесь возможны два случая, связанные со сходимостью ряда:

1),

тогда стационарные вероятности существуют и равны

.

2),

тогда не существует стационарного распределения для рассматриваемого процесса гибели и размножения.

1.8. Процесс чистого размножения

Далее рассмотрим нестационарный процесс чистого размножения, когда все µ_j = 0. Для n > i найдём T_in. Система (2) в этом случае имеет вид

1 – λ_iT_in+ λ_iT_i+1n = 0,

откуда получим

.

Рассмотрим среднее значение времени перехода процесса чистого размножения в состояние с бесконечно большим номером, то есть

.

Здесь также возможны два случая, связанные со сходимостью ряда.

1) Если ряд расходится, то это означает, что в состояние с бесконечно большим номером система перейдёт за бесконечно большое время. Этот случай вполне естественный.

2) Если же ряд , это соответствует тому, что система за конечное время переходит в состояние с бесконечно большим номером. В физике это соответствует неуправляемой цепной реакции (взрыв), а для биологических систем – явлению эпидемии.

1.8. Пуассоновский процесс

Рассмотрим процесс m(t), который называется пуассоновским и является цепью Маркова с непрерывным временем, точнее нестационарным процессом чистого размножения. Для вероятностей

P_m(t) = {m(t) = m}

система дифференциальных уравнений Колмогорова имеет вид

,

.

1.9. Метод производящих функций

Для решения этой системы дифференциально-разностных уравнений воспользуемся методом производящих функций, обозначив

,

систему уравнений Колмогорова перепишем в виде уравнения

,

дополнив которое начальным условием

G(z,0) = 1,

решение G(z,t) запишем в виде

,

откуда получим, что вероятности P_m(t) имеют вид

,

то есть вид пуассоновского распределения с параметром λt, что оправдывает название случайного процесса.