4.7.2. Решение уравнения (12) методом матричной экспоненты
Однородную систему линейных дифференциальных уравнений (12) с постоянными коэффициентами можно также решать методом матричной экспоненты, поэтому имеет место следующее утверждение.
Теорема 2. Распределение вероятностей
P(m, t) = P(m(t) = m).
числа событий, наступивших в MAP-потоке за время t, определяется следующим равенством
,
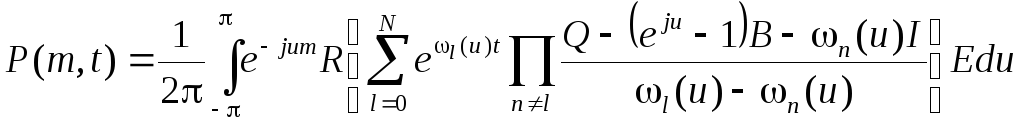(20)
где n(u) – собственные числа матрицы Q – (eju – 1)B.
Доказательство.
Решение системы (12), удовлетворяющее начальному условию (13), можно записать в виде произведения начального вектора R и матричной экспоненты
.
(21)
Значения матричной экспоненты можно определять либо суммой матричного ряда, либо применяя формулу Сильвестра, которая в общем виде записывается следующим образом
,
где n – собственные числа матрицы A.
Применяя формулу Сильвестра к матричной экспоненте в равенстве (21), получим равенство
,
определяющее скалярную характеристическую функцию
h(u, t) = Mejum(t) = H(u, t)E
числа событий, наступивших в потоке за время t
.
Применяя к этой характеристической функции обратное преобразование Фурье по переменной u, получим равенство (20).
Теорема доказана.
4.7.3. Исследование модели полумарковского потока
Основное уравнение для полумарковского потока имеет вид
.
(22)
Для нахождения его частного решения определим начальное условие в виде
H(z, u, 0) = R(z),
где R(z) – стационарное распределение вероятностей значений двумерного случайного процесса {s(t), z(t)}.
Нахождение распределения r(z)
Докажем следующее утверждение.
Лемма. Распределение вероятностей R(z) определяется равенством
,
(23)
где
производная в нуле
имеет вид
,
(24)
здесь распределение вероятностей r является решение системы уравнений
r = rP, rE = 1, (25)
а величина определяется равенством
.
(26)
Доказательство.
Так как для R(z) выполняется также тождество
R(z) ≡ H(z, 0. t),
то вектор R(z) является решением, полученного из (22), уравнения
,
поэтому его можно записать в виде
,
совпадающем
с (23). Здесь необходимо найти вектор
.
Так как компоненты R(s, z) вектора R(z) по определению равны
R(s, z) = P{s(t) = s, z(t) < z},
то
R = R(∞) = {P[s(t) = s]},
поэтому из (23) получим
.
(27)
В силу необходимого условия сходимости несобственного интеграла можно записать равенство нулю подынтегрального выражения при x →∞, получим систему уравнений
(28)
для
компонент вектора
,
здесь P = A(∞).
Так как систему (28) совпадает с системой уравнений Колмогорова для стационарного распределения вероятностей r значений вложенной цепи Маркова, то выполняется равенство
,
совпадающее с (24), где λ – некоторая мультипликативная постоянная, значение которой найдём следующим образом.
Подставляя (24) в (27), получим
,
здесь использовано равенство r = rP.
Так как в силу условия нормировки RE = 1, то получаем равенство
,
совпадающее с (26).
Лемма доказана.
Отметим, что F(x) является функцией распределения длин интервалов SM-потока.