3.2. Методы исследования полумарковских процессов
3.2.1. Метод дополнительной переменно для исследования процесса марковского восстановления
Пусть для процесса марковского восстановления k(t), заданного стохастической матрицей Р и набором функций распределения Ak(x), требуется найти стационарное распределение вероятностей P(k) = P{k(t) = k}.
В силу того, что процесс k(t) марковским не является, определим случайный процесс z(t) – длину интервала от момента t до момента очередного отказа (замены элемента). Тогда двумерный процесс {k(t), z(t)} является марковским, поэтому для его распределения вероятностей
P(k,z,t) = P{k(t) = k, z(t) < z}
можно записать следующие равенства
Здесь
разность P(k,z,t)
– P(k,Δt,t)
характеризует то, что за время Δt
процесс k(t)
не изменил состояния, а величина z(t)
лежит в интервале от Δt
до z,
сумма
показывает, что за время Δt
процесс k(t)
перешел из состояния v
≠ k
в состояние k.
Последнее равенство перепишем в виде
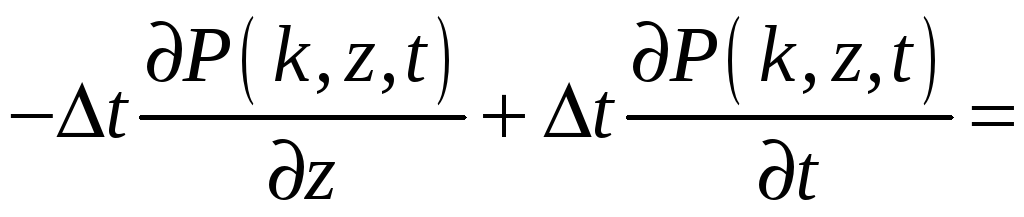
Разделим левую и правую части на Δt
,
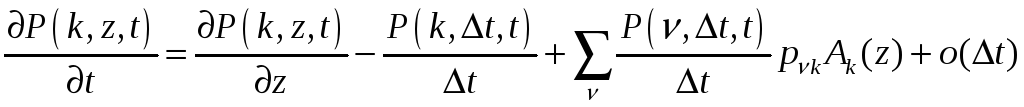где
.
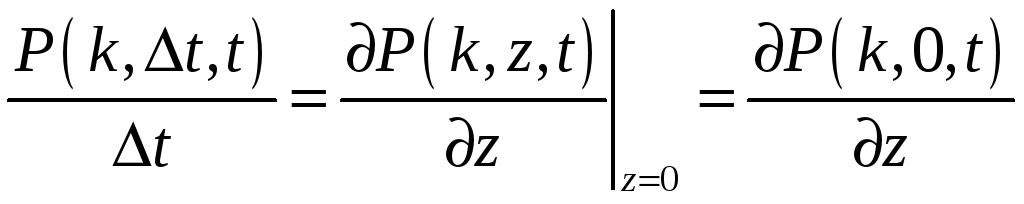Тогда получим равенство
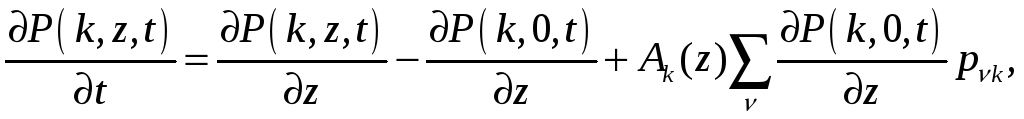
которое для стационарного распределения P(k,z,t) = P(k,z) перепишем в виде
Интегрируя левую и правую части этого равенства, получим
.
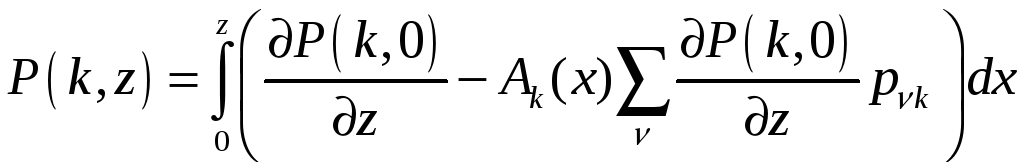В силу условия согласованности вероятностных распределений, одномерное распределение Р(k) запишем следующим образом
.
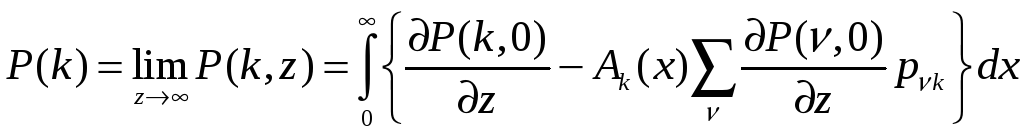(7)
Так как подынтегральная функция является монотонной, то можно записать следующее равенство
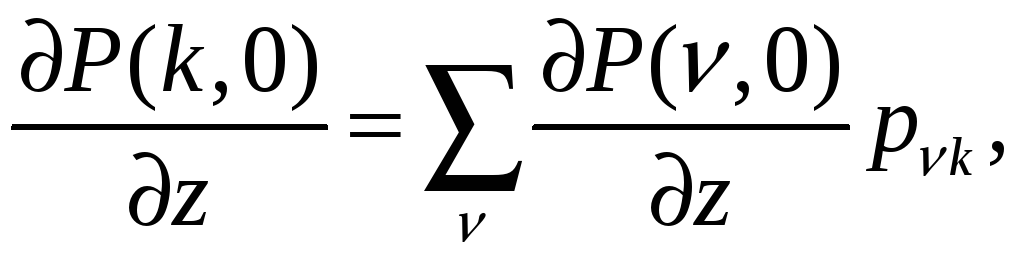
которое совпадает с системой уравнений Колмогорова
для стационарного распределения вероятностей r(k) состояний вложенной цепи Маркова (n), поэтому
(8)
Мультипликативную постоянную C найдём из условия нормировки. Применяя равенство (8), перепишем (7)
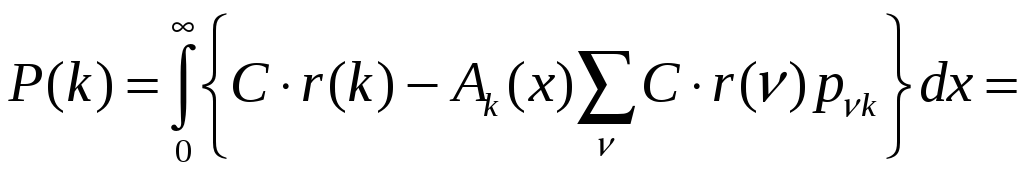
где ak – среднее значение срока службы элемента вида k. Таким образом
P(k) = C r(k) ak
а в силу условия нормировки запишем
откуда получим
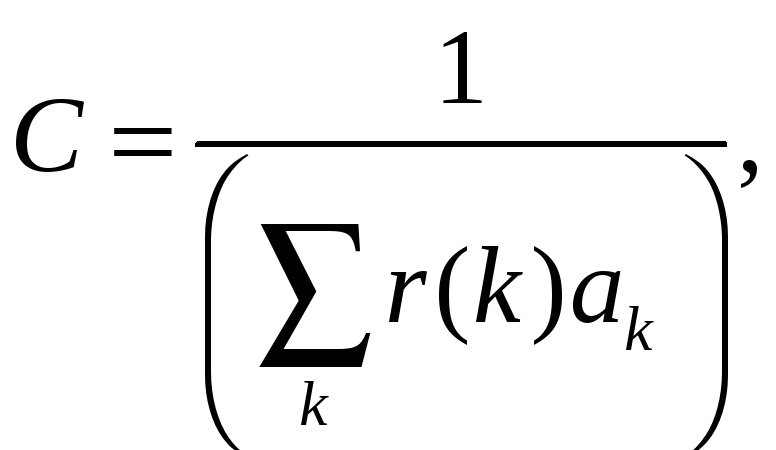
следовательно, стационарное распределение вероятностей P(k) значений процесса марковского восстановления k(t) имеет вид
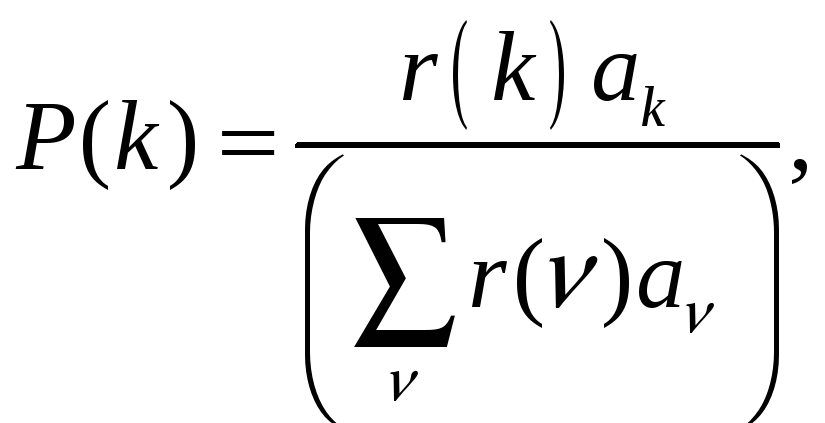(9)
где ak – среднее значение срока службы элемента вида k
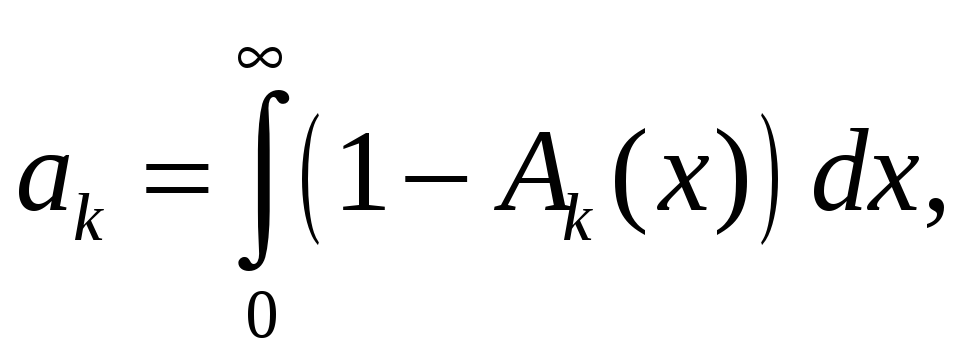
r(k) – стационарное распределение вероятностей состояний вложенной цепи Маркова (n).
3.2.2. Исследование полумарковского процесса методом дополнительной переменной y(t)
Пусть для полумарковского процесса k(t), заданного полумарковской матрицей A(x) необходимо найти стационарное распределение вероятностей P(k) = P{k(t) = k}.
Для исследования полумарковского процесса k(t), определяемого полумарковской матрицей A(x), применение случайного процесса z(t) требует введения ещё одной дополнительной переменной, поэтому рассмотрим случайный процесс y(t), равный длине интервала от момента последнего отказа (замены элемента) до текущего момента времени t. В этом случае двумерный процесс {k(t), y(t)} является марковским процессом.
Обозначим
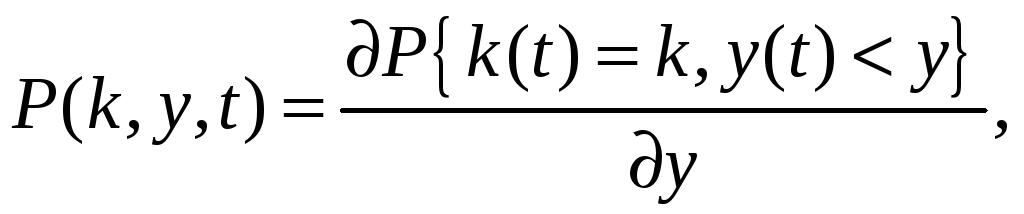(10)
тогда для этого распределения вероятностей можно при tn < t < tn+1 = tn + (n+1) записать следующее равенство
,
из которого получим уравнение
.
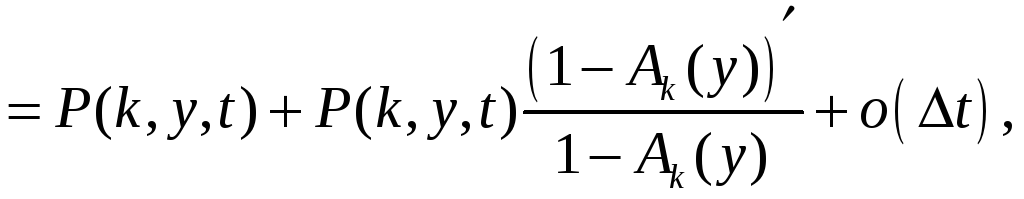
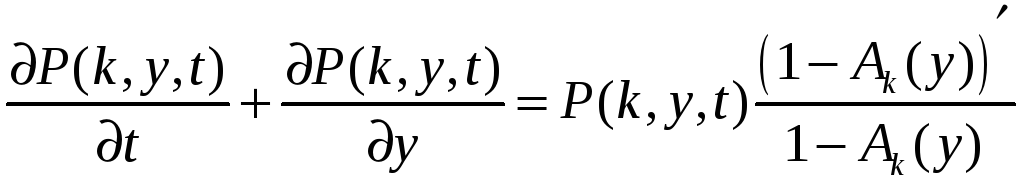Для стационарного распределения P(k,y,t) = P{k,y} это уравнение перепишем в виде
.
(11)
Для нахождения частного решения этого уравнения необходимо записать краевое по y условие для решения P(k,y) уравнения (11). Такое краевое условие получим следующим образом. При tn<t<tn+1=tn+(n+1) в силу (10) можно записать
.
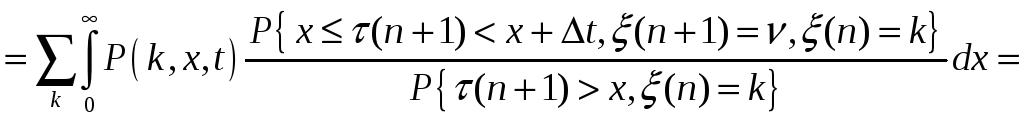
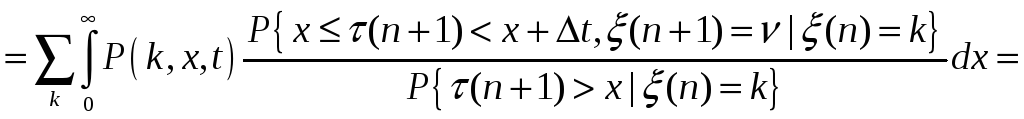
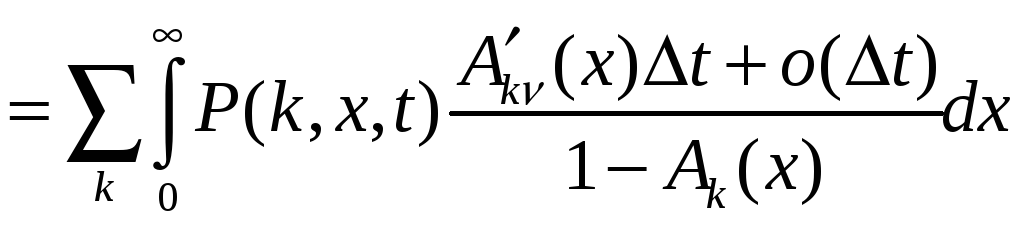Поделив левую и правую части этого равенства на t и полагая, что t сходится к нулю, получим равенство
,
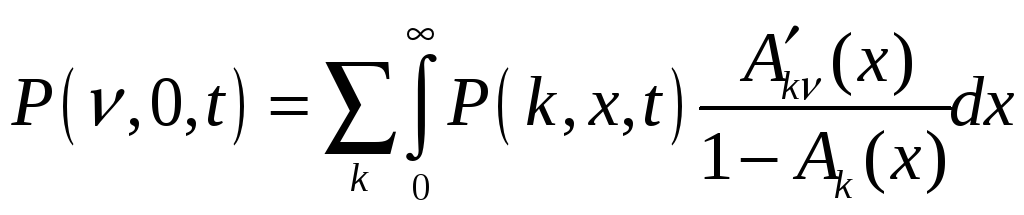которое в стационарном режиме имеет вид
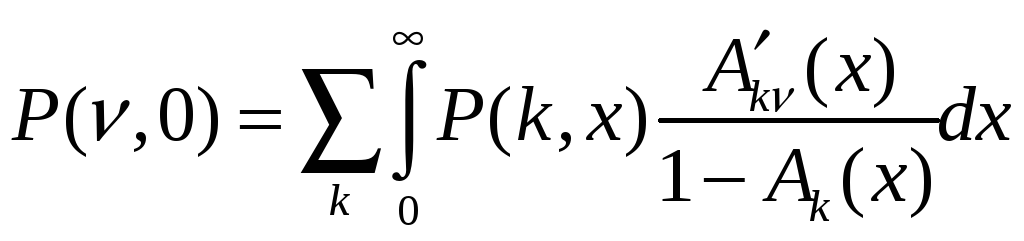(12)
и определяет краевое условие при y = 0 для решения P(k,y) уравнения (11). Общее решение уравнения (11) можно записать в виде
. (13)
Для определения постоянных C(k), воспользуемся краевым условием (12), подставив в которое (13), получим равенство
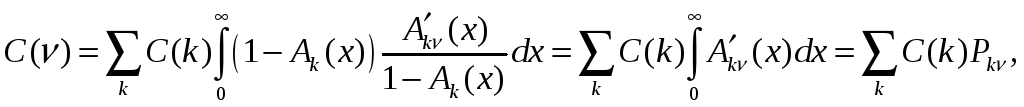
которое совпадает с системой уравнений Колмогорова для стационарного распределения вероятностей r(k) значений вложенной цепи Маркова, поэтому
,
и в силу (13) запишем
.
В силу определения (10) функций P(k,y) и условия согласованности распределений одномерное маргинальное распределение P(k) имеет вид
. (14)
Отметим, что распределение (14) для полумарковского процесса совпадает с распределением вероятностей (9) для процесса марковского восстановления.