-
Сортировка простым включением
В этой сортировке массив делится на 2 части: отсортированную и неотсортированную. На каждом шаге берется очередной элемент из неотсортированной части и «включается» в отсортированную часть массива.
Пусть отсортировано начало массива A[1], A[2], ..., A[i-1], а остаток массива A[i], ...,A[n] содержит неотсортированную часть. На очередном шаге будем включать элемент A[i] в отсортированную часть, ставя его на соответствующее место. При этом придется сдвинуть часть элементов, больших A[i], (если таковые есть) на одну позицию правее, чтобы освободить место для элемента A[i]. Но при сдвиге будет потеряно само значение A[i], поскольку в эту позицию запишется первый (самый правый – с самым большим индексом) сдвигаемый элемент. Поэтому прежде чем производить сдвиг элементов необходимо сохранить значение A[i] в промежуточной переменной.
Так как массив из одного элемента можно считать отсортированным, начнем с i=2.
Выглядит это в виде следующей процедуры.
procedure InsertSort(n: integer;
var A: array[1..n] of integer);
{Процедура сортировки простым включением}
var
i, j, Tmp: integer;
begin
for i := 2 to n do begin
{Сохраняем текущий элемент}
Tmp := A[i];
{Сдвигаем элементы, большие, чем текущий}
j := i-1;
while (A[j] > Tmp) and (j > 1) do begin
A[j+1] := A[j];
j := j-1;
end;
{Вставляем текущий элемент}
A[j+1] := Tmp;
end;
end;
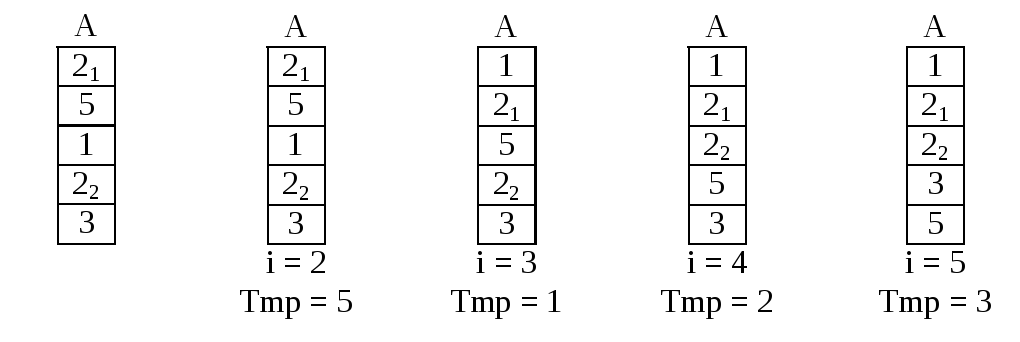
Рисунок 41. Сортировка простым включением
Этот алгоритм также имеет максимальную и среднюю временную сложности, пропорциональные O(n2), но в случае исходно отсортированного массива внутренний цикл не будет выполняться ни разу, поэтому метод имеет временную сложность Tmin(n), пропорциональную O(n). Можно заметить, что метод использует любой частичный порядок, и чем в большей степени массив исходно упорядочен, тем быстрее он закончит работу. В отличие от предыдущего метода, этот не требует дополнительной памяти, но сохраняет порядок элементов с одинаковыми значениями.
-
Сортировка методом Шелла
Метод Шелла является усовершенствованием метода простого включения, который основан на том, что включение использует любой частичный порядок. Но недостатком простого включения является то, что во внутреннем цикле элемент A[i] фактически сдвигается на одну позицию. И так до тех пор, пока он не достигнет своего места в отсортированной части. (На самом деле передвигалось место, оставленное под A[i]). Метод Шелла позволяет преодолеть это ограничение следующим интересным способом.
Вместо включения A[i] в подмассив предшествующих ему элементов, его включают в подсписок, содержащий элементы A[i-h], A[i-2h], A[i-3h] и так далее, где h – положительная константа. Таким образом, формируется массив, в котором «h – серии» элементов, отстоящих друг от друга на h, сортируются отдельно.
Конечно, этого недостаточно: процесс возобновляется с новым значением h, меньшим предыдущего. И так до тех пор, пока не будет достигнуто значение h=1.
В настоящее время неизвестна последовательность hi, hi-1, hi-2, ..., h1, оптимальность которой доказана. Для достаточно больших массивов рекомендуемой считается такая последовательность, что hi+1=3hi+1, а h1=1. Начинается процесс с hm, что hm[n/9]. Иногда значение h вычисляют проще: hi+1=hi/2, h1=1, hm=n/2. Это упрощенное вычисление h и будем использовать далее.
Теперь запишем алгоритм.
procedure ShellSort(n: integer;
var A: array[1..n] of integer);
{Процедура сортировки Шелла}
var
h, i, j, Tmp: integer;
begin
{Вычисляем величину h}
h := n div 2;
{Собственно сортировка}
while h > 0 do begin
for i := 1 to n-h do begin
j := i;
while j > 0 do begin
{Сравниваем элементы, отстоящие друг от друга}
{на расстояние, кратное h}
if A[j] > A[j+h] then begin
{Меняем элементы}
Tmp := A[j+h];
A[j+h] := A[j];
A[j] := Tmp;
j := j - h;
end else begin
{Досрочно завершаем цикл с параметром j}
j := 0;
end;
end;
end;
{Уменьшаем размер серии}
h := h div 2;
end;
end;
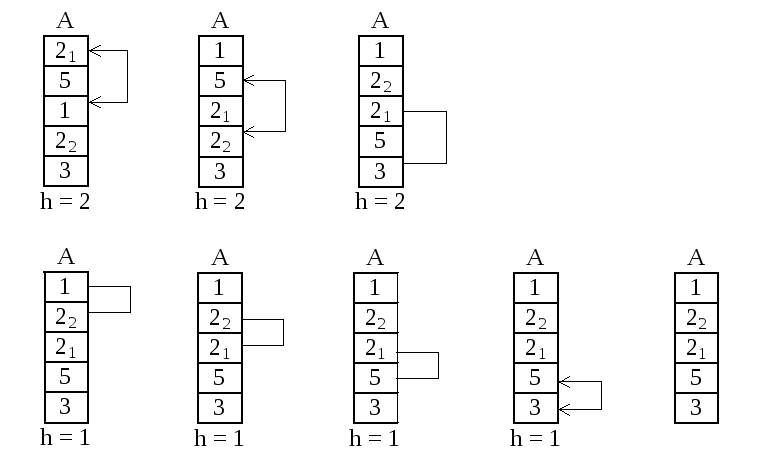
Рисунок 42. Сортировка Шелла
Как показывают теоретические выкладки, которые здесь приводить не будем, сортировке методом Шелла требуется в среднем 1,66n1,25 перемещений. Порядок элементов влияет на количество итераций внутреннего цикла while. Дополнительной памяти данный алгоритм не требует, но и не гарантирует сохранение порядка элементов с одинаковыми значениями.