4. Сбалансированные по высоте деревья поиска

Как уже говорилось ранее (см. п. 3.3.4.2), в худшем случае (дерево вырождено в линейный список) хранение данных в упорядоченном бинарном дереве никакого выигрыша в сложности операций (поиск/добавление/удаление) по сравнению с массивом или линейным списком не дает. В лучшем случае (дерево сбалансировано) для всех операций получается логарифмическая сложность, что гораздо лучше.

Идеально сбалансированным называется дерево, у которого для каждой вершины выполняется требование: число вершин в левом и правом поддеревьях различается не более чем на 1. Однако идеальную сбалансированность довольно трудно поддерживать. В некоторых случаях при добавлении/удалении может потребоваться значительная перестройка дерева, не гарантирующая логарифмической сложности. Поэтому в 1962 году два советских математика Г.М. Адельсон-Вельский и Е.М. Ландис ввели менее строгое определение сбалансированности и доказали, что при таком определении можно написать программы добавления/удаления, имеющие логарифмическую сложность и сохраняющие дерево сбалансированным.

Дерево считается сбалансированным по АВЛ (в дальнейшем просто «сбалансированным»), если для каждой вершины выполняется требование: высота левого и правого поддеревьев различаются не более, чем на 1. Не всякое сбалансированное дерево идеально сбалансировано, но всякое идеально сбалансированное дерево сбалансировано.

При операциях добавления и удаления может произойти нарушение сбалансированности дерева. В этом случае потребуются некоторые преобразования, не нарушающие упорядоченности дерева и способствующие лучшей сбалансированности.

Рассмотрим такие преобразования.

Пусть вершина a имеет правого потомка b. Обозначим через P левое поддерево вершины a, через Q и R – левое и правое поддеревья вершины b. Упорядоченность дерева требует, чтобы P < a < Q < b < R. Точно того же требует упорядоченность дерева с корнем b, его левым потомком a, в котором P и Q – левое и правое поддеревья a, R – правое поддерево b. Поэтому первое дерево можно преобразовать во второе, не нарушая упорядоченности. Такое преобразование называется малым правым вращением. Аналогично определяется симметричное ему малое левое вращение.

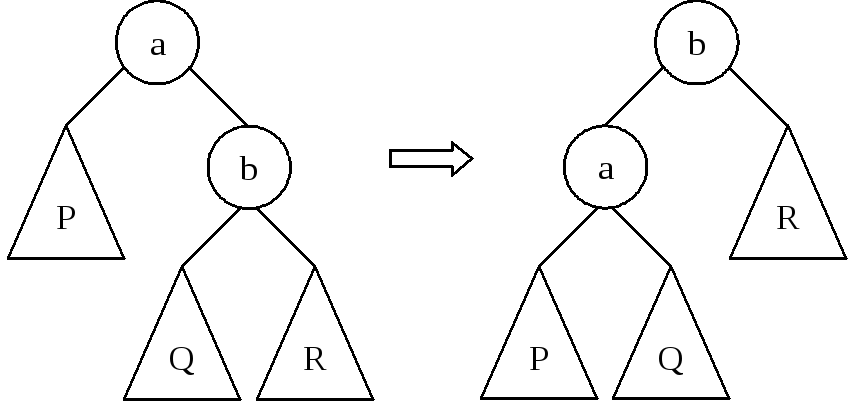
Рисунок 33. Малое правое вращение сбалансированного дерева

Пусть b – правый потомок a, c – левый потомок b, P – левое поддерево a, Q и R – левое и правое поддеревья c, S – правое поддерево b. Тогда P < a < Q < c < R < b < S. Такой же порядок соответствует дереву с корнем c, имеющим левого потомка a и правого потомка b, для которого P и Q – поддеревья вершины a, а R и S – поддеревья вершины b. Соответствующее преобразование будем называть большим правым вращением. Аналогично определяется симметричное ему большое левое вращение.

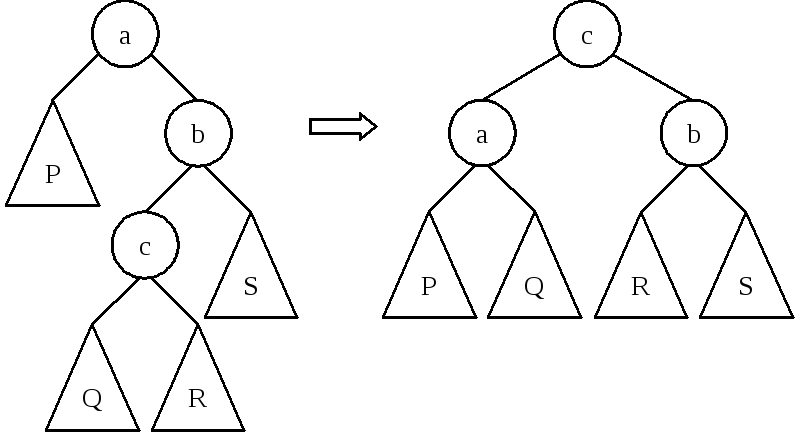
Рисунок 34. Большое правое вращение сбалансированного дерева

Теперь приведем алгоритм балансировки на языке Паскаль. В этом алгоритме опущены левые вращения (большое и малое), которые записываются симметрично.

Предварительно договоримся, что в каждой вершине дерева помимо значения элемента будем хранить показатель сбалансированности в данной вершине. Показатель сбалансированности вершины – это разница между высотами правого и левого поддеревьев данной вершины.

type

PTree = ^TTree;

TTree = record

Data: TypeElement; {поле данных}

Left, Right: PTree; {указатели на левое и правое поддеревья}

Balance: integer; {показатель сбалансированности}

end;

В сбалансированном дереве показатели сбалансированности всех вершин лежат в пределах от -1 до 1. При операциях добавления/удаления могут появляться вершины с показателями сбалансированности -2 и 2.

procedure TreeBalance(a: PTree; var CurBalance: integer);

{Балансировка двоичного дерева}

procedure SmallRightRotation(a: PTree);

{малое правое вращение поддерева с корнем a}

var

b: PTree;

val_a, val_b: TypeElement;

h_P, h_Q, h_R: integer;

begin

b := a^.Right; {b <> null}

val_a := a^.Data; val_b := b^.Data;

h_Q := 0;

h_R := b^.Balance;

h_P := (max(h_Q, h_R) + 1)- a^.Balance;

a^.Data := val_b; b^.Data := val_a;

a^.Right := b^.Right; {поддерево R}

b^.Right := b^.Left; {поддерево Q}

b^.Left := a^.Left; {поддерево P}

a^.Left := b;

b^.Balance := h_Q - h_P;

a^.Balance := h_R - (max(h_P, h_Q) + 1);

end;

procedure BigRightRotation(a: PTree);

{большое правое вращение поддерева с корнем a}

var

b, c: PTree;

val_a, val_b, val_c: TypeElement;

h_P, h_Q, h_R, h_S: integer;

begin

b := a^.Right; c := b^.Left; {b <> null,c <> null}

val_a := a^.Data; val_b := b^.Data; val_c := c^.Data;

h_Q := 0; h_R := c^.Balance;

h_S := (max(h_Q, h_R) + 1) + b^.Balance;

h_P := 1 + max (h_S, h_S-b^.Balance) - a^.Balance;

a^.Data := val_c; c^.Data := val_a;

b^.Left := c^.Right; {поддерево R}

c^.Right := c^.Left; {поддерево Q}

c^.Left := a^.Left; {поддерево P}

a^.Left := c;

b^.Balance := h_S - h_R;

c^.Balance := h_Q - h_P;

a^.Balance := max(h_S, h_R) - max(h_P, h_Q);

end;

begin {-2 <= a^.Balance <= 2}

if a^.Balance = 2 then begin

b := a^.Right;

if b^.Balance = -1 then begin

BigRightRotation(a); CurBalance := -1;

end else begin

if b^.Balance = 0 then begin

SmallRightRotation(a); CurBalance := 0;

end else begin {b^.Balance = 1}

SmallRightRotation(a); CurBalance := - 1;

end;

end;

end else begin

if a^.Balance = -2 then begin

b := a^.Left;

if b^.Balance = 1 then begin

BigLeftRotation(a); CurBalance := -1;

end else begin

if b^.Balance = 0 then begin

SmallLeftRotation(a); CurBalance := 0;

end else begin {b^.Balance = -1}

SmallLeftRotation(a); CurBalance := - 1;

end;

end;

end else begin {-2 < a^.Balance < 2, ничего делать не надо}

CurBalance := 0;

end;

end;

end;

Схематично алгоритм добавления нового элемента в сбалансированное дерево будет состоять из следующих трех основных шагов:

1. поиск по дереву.

2. вставка элемента в место, где закончился поиск, если элемент отсутствует.

3. восстановление сбалансированности.

Первый шаг необходим для того, чтобы убедиться в отсутствии элемента в дереве, а также найти такое место вставки, чтобы после вставки дерево осталось упорядоченным. Первые два шага ничем не отличаются от алгоритмов, приведенных в п. 3.3.4.1.

Третий шаг представляет собой обратный проход по пути поиска: от места добавления к корню дерева. По мере продвижения по этому пути корректируются показатели сбалансированности проходимых вершин, и производится балансировка там, где это необходимо. Добавление элемента в дерево никогда не требует более одного поворота.

Алгоритм удаления элемента из сбалансированного дерева будет выглядеть так:

1. поиск по дереву.

2. удаление элемента из дерева.

3. восстановление сбалансированности дерева (обратный проход).

Первый шаг необходим, чтобы найти в дереве вершину, которая должна быть удалена. Первых два шага аналогичны удалению элемента, приведенному в п. 3.3.4.1.

Третий шаг представляет собой обратный проход от места, из которого взят элемент для замены удаляемого, или от места, из которого удален элемент, если в замене не было необходимости.

Операция удаления может потребовать перебалансировки всех вершин вдоль обратного пути к корню дерева, то есть порядка log n вершин.

Таким образом, алгоритмы поиска, добавления и удаления элементов в сбалансированном дереве имеют сложность, пропорциональную O(log n).

Г.М. Адельсон-Вельский и Е.М. Ландис доказали теорему, согласно которой высота сбалансированного дерева никогда не превысит высоту идеально сбалансированного дерева более, чем на 45%.