Тема 3. Интерполяция и приближение полиномами Лабораторная работа № 6 интерполяционный многочлен лагранжа

Цель работы: изучить метод построения для табличной функции y(x) интерполяционного полинома в форме полинома Лагранжа, сравнить результаты интерполирования для функции F(x) в случае выбора произвольной сетки узлов интерполирования и в случае выбора узлов Чебышева, оценить погрешность интерполирования.

Постановка задачи

1. Изучить теоретические сведения.

2. Построить для заданной табличной функции y(x) аналитическую функцию в виде интерполяционного многочлена Лагранжа. Выполнить поставленную задачу в средах MATHCAD и MATLAB.

3. Определить значение функции в средних точках интервалов , , .

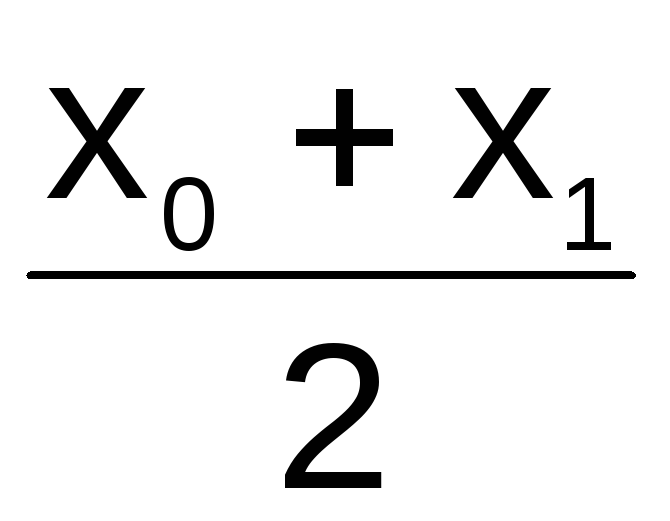4. Проверить результаты с помощью встроенных функций интерполяции.

5. Представить полученные результаты графически.

6. Задать самостоятельно дробно-рациональную функцию F(x) специального вида. Сравнить с помощью графиков результаты интерполирования для функции F(x) в случае выбора произвольной сетки узлов интерполирования и в случае выбора узлов Чебышева.

7. Найти значение функции F(x) в промежуточной точке на интервале интерполирования. Оценить погрешность замены функции интерполяционным многочленом.

8. Применить встроенные функции пакета MATLAB для решения реальной задачи интерполирования (данные взять из файла file.dat).

Содержание отчёта

1. Теоретические сведения.

2. Таблица значений исходной функции Y(x).

3. Запись интерполяционного многочлена Р(x) для заданной табличной функции (без приведения подобных).

4. Листинги для решения задачи построения интерполяционного многочлена Лагранжа в пакетах MATHCAD и MATLAB.

5. Таблица значений исходной функции F(x) (задать самостоятельно).

6. Сравнительный анализ результатов интерполирования для функции F(x) в случае выбора произвольной сетки узлов интерполирования и в случае выбора узлов Чебышева.

7. Вычисление погрешности интерполирования для произвольной точки функции F(x) (в пакете MATHCAD).

8. Решение задачи интерполирования для таблицы данных файла file.dat. Графики результата интерполирующего многочлена.

9. Выводы.

Теоретические сведения

Для произвольно заданных узлов интерполирования пользуются формулой, обычно называемой интерполяционной формулой Лагранжа.

_{Пусть на отрезке [a,b] заданы точки xk, k=0,1,…,n (узлы интерполирования), в которых известны значения функции f(x). Задача интерполирования алгебраическими многочленами состоит в том, чтобы построить многочлен степени n}

_{, (6.1)}

_{значения которого в заданных точках совпадают со значениями функции f(x) в этих точках:}

_(6.2)

_{Для любой непрерывной функции f(x) сформулированная задача имеет единственное решение. Действительно, для отыскания коэффициентов a0,a1,…,an получаем систему линейных уравнений}

_,

_{определитель которой (определитель Вандермонда) отличен от нуля, если среди точек xi, i=0,1,…,n нет совпадающих. Решение системы можно записать различным образом.}

_{Интерполяционный многочлен, представленный в виде}

_(6.3)

_{называется интерполяционным многочленом Лaгранжа (Жозеф Луи Лагранж — французский математик). Функции wi есть многочлены степени n, которые называются лагранжевыми коэффициентами:}

_(6.4)

Рассмотрим два частных случая интерполяционного полинома Лагранжа.

1. При имеем две узловые точки. Формула Лагранжа представляет в этом случае уравнение прямой , проходящей через две заданные точки:

,

где — абсциссы этих точек.

2. При получим уравнение параболы , проходящей через три точки:

,

где — абсциссы данных точек.

Отметим преимущества и недостатки многочлена Лагранжа.

Преимущества: интерполяционный многочлен Лагранжа работает как для таблиц с постоянным шагом, так и для таблиц с переменным шагом; р_ni(x) не зависит от функции f(x), откуда следует, что по одной системе узлов можно интерполировать несколько функций.

Недостатки: все слагаемые в формуле Лагранжа равнозначны, поэтому при добавление узлов таблицы многочлен Лагранжа придется полностью перестраивать.

Погрешность интерполяционной формулы Лагранжа удовлетворяет неравенству

,

где , , .

Величину ошибки можно минимизировать, если в качестве узлов интерполяции выбрать абциссы (узпы) полинома Чебышева. Многочлен Чебышева Tn(x) на интервале [-1,1] имеет ровно n действительных корней, определяемых как . Для того чтобы решить задачу интерполяции на интервале [a,b], необходимо выполнить линейное преобразование.