Содержание отчета

1. Теоретические сведения.

2. Таблица ручного счета для решения системы уравнений.

3. Листинги расчета на ЭВМ.

4. Выводы.

Теоретические сведения

Одним из наиболее распространенных методов решения систем линейных уравнений является метод Гаусса. Он может быть осуществлен с помощью разных вычислительных схем, в основе которых лежит одна и та же идея последовательного исключения неизвестных. Метод Гаусса является точным, т.е. если коэффициенты при неизвестных и правые части системы – точные числа, а все вычисления производятся без округлений, то в ответе получим точные значения неизвестных. Рассмотрим подробнее схему единственного деления.

Схема единственного деления. Для простоты рассуждений ограничимся рассмотрением системы трех уравнений с тремя неизвестными. Эти же приемы могут быть применены для системы уравнений любого порядка.

Требуется найти решение системы

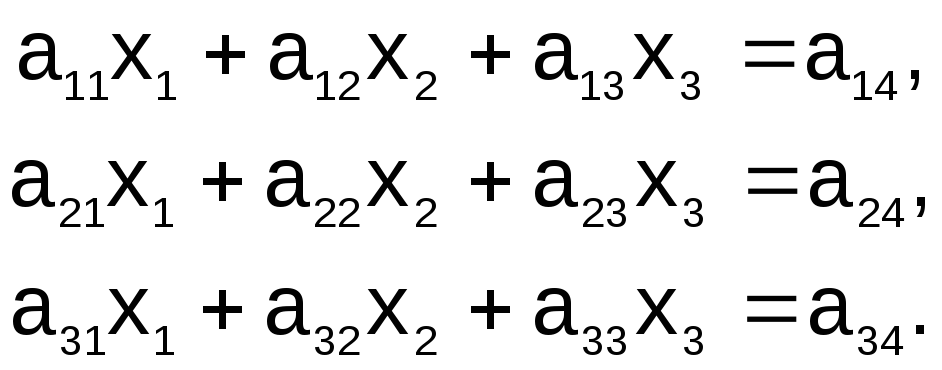(4.1)

Пусть . В противном случае уравнения переставляются так, чтобы это условие выполнялось. Разделим первое уравнение системы (4.1) на коэффициент , который будем называть «ведущим» элементом. Получим уравнение

, (4.2)

где

.

Пользуясь уравнением (4.2), можно исключить переменную х₁ из второго и третьего уравнений системы (4.1). Для этого из второго уравнения системы (4.1) вычитаем уравнение (4.2), умноженное на , а из третьего уравнения системы (4.1) вычитаем уравнение (4.2), умноженное на .

Приходим к системе

(4.3)

где

.

К полученной системе (4.3) применим те же преобразования, что и к системе (4.1). Делим первое уравнение системы на «ведущий» элемент . Получаем уравнение

, (4.4)

где

.

Исключаем переменную х₂ из второго уравнения системы (4.4). Для этого умножаем уравнение (4.4) на и вычитаем из второго уравнения системы (4.3). Получаем

, (4.5)

где .

Наконец, разделив уравнение (4.5) на , имеем

. (4.6)

Объединив уравнения (4.2), (4.4) и (4.6) с коэффициентами b, получим треугольную систему, эквивалентную данной:

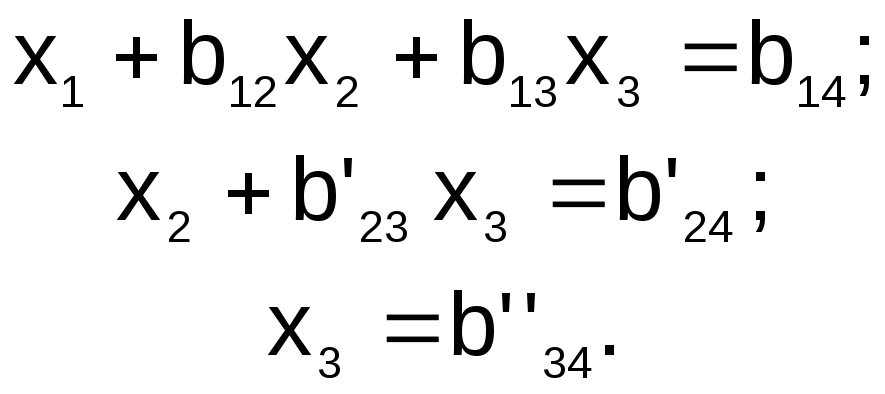(4.7)

Решение системы (4.7) и, следовательно, системы (4.1) записывается в виде

(4.8)

Итак, для решения системы (4.1) сначала строим вспомогательную треугольную систему (4.7), а затем по формулам (4.8) записываем решение системы. Процесс нахождения коэффициентов треугольной системы называется прямым ходом, а процесс получения ее решения – обратным ходом. Во избежание накопления погрешностей округления весь расчет ведем с двумя запасными знаками, которые при записи решения системы отбрасываем.

Расчетные формулы метода Гаусса в общем виде можно записать следующим образом. На некотором k-м этапе (k = 1,…,n-1) исключаем х_k с помощью преобразований, причем предполагаем, что :

(,).

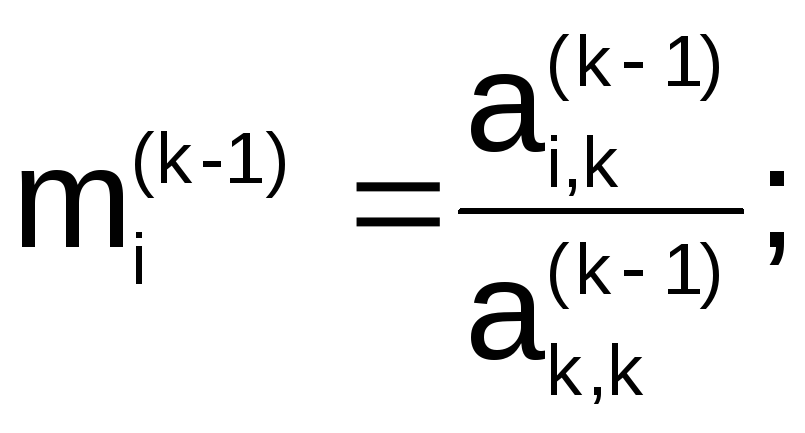
Отметим, что А = {} – расширенная матрица коэффициентов (образуется из матрицы коэффициентов добавлением столбца свободных членов).

Обратный ход для нахождения неизвестных задается формулой

, .

Применение метода Гаусса для вычисления определителя. Доказано, что определитель матрицы А равен произведению «ведущих» (или главных) элементов в соответствующей схеме Гаусса, т.е.

.

Таким образом, для вычисления определителя нужно выполнить вычисления, необходимые для осуществления прямого хода в методе Гаусса для системы , а затем найти произведение «ведущих» элементов. Вычислительная схема в этом случае такая же, как и для решения системы линейных уравнений, но только без столбца свободных членов.

Применение метода Гаусса для вычисления обратной матрицы. Обратной к матрице А называют такую матрицу , для которой выполняется условие

, (4.9)

где I – единичная матрица,

.

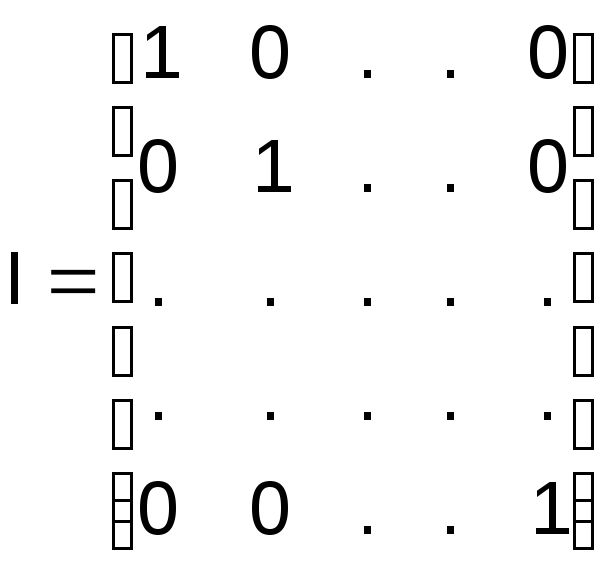Квадратная матрица называется неособенной, или невырожденной, если ее определитель отличен от нуля. Всякая неособенная матрица имеет обратную.

Для вычисления элементов обратной матрицы используем соотношение (4.9). Умножая матрицу А на матрицу и приравнивая каждый элемент произведения соответствующему элементу единичной матрицы I, получаем систему из n² уравнений с n² неизвестными. Все эти системы имеют одну и ту же матрицу коэффициентов А и отличаются только свободными членами. Так как при решении системы по методу Гаусса основные вычисления приходится производить над матрицей коэффициентов, решение всех этих систем можно объединить в одной схеме, рассматривая одновременно n столбцов свободных членов.

Число арифметических операций N, необходимых для реализации метода Гаусса, определяется следующей формулой:

,

где n – число неизвестных. Таким образом, число арифметических операций примерно пропорционально кубу числа неизвестных.

Алгоритм неприменим, когда какой-либо из ведущих элементов равен нулю или имеет близкое к нулю значение. В этом случае следует использовать модифицированный метод Гаусса, в котором в качестве ведущего элемента на каждом шаге исключения неизвестных выбирается максимальный по модулю элемент матрицы коэффициентов. Это приводит к необходимости переименовывать неизвестные, но устойчивость метода повышается.