5.3.2. Метод Ньютона

Пусть известно начальное приближение х₀ корня уравнения. Метод Ньютона (метод касательных) заключается в построении итерационной последовательности

,

сходящейся к корню уравнения х*.

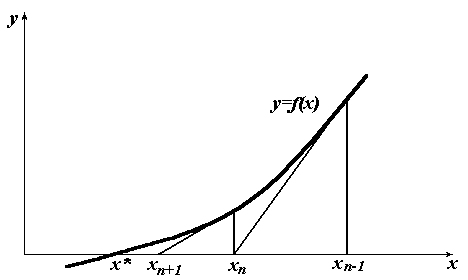
Рис. 5.3. Метод Ньютона

Если функция f(х) определена и дважды дифференцируема на отрезке [а; b], причем на концах отрезка она принимает значения разных знаков , а производные и не меняют знак на отрезке [a; b], тогда, исходя из начального приближения х₀, удовлетворяющего неравенству (в качестве начального приближения выбирается тот конец отрезка, на котором функция по знаку совпадает со своей второй производной), можно построить указанную итерационную последовательность, сходящуюся к единственному на этом отрезке корню функции f.

Метод Ньютона допускает простую геометрическую интерпретацию. Очередное приближение представляет собой абсциссу точки пересечения касательной к графику функции в точке с осью ОХ (рис. 5.3).Если по каким-либо причинам невозможно каждый раз считать производные и значения функций в точках, то допустимо каждый раз вместо f^/(x_k-1) брать f^/(x₀), т.е. производную в начальной точке.

Рассмотрим модификацию метода Ньютона для решения нелинейных систем. Пусть имеется нелинейное уравнение , где f – вектор-функция, т.е. дана система

Предположим, что в любой точке шара матрица Якоби рассматриваемой системы

невырождена, т.е. . Тогда в каждой точке шара существует обратная матрица и последовательность приближений строится следующим образом:

.

Для решения систем нелинейных уравнений лучше всего использовать метод Ньютона. Если точные значения частных производных найти не удается, можно пользоваться их приближенными значениями, найденными методом секущих.

5.4. Решение дифференциальных уравнений

Обыкновенные дифференциальные уравнения (ОДУ) широко используются для математического моделирования процессов и явлений в различных областях науки и техники. Переходные процессы в радиотехнике, кинетика химических реакций, динамика биологических популяций, модели экономического развития исследуются с помощью ОДУ.

5.4.1. Постановка задачи. Разностные схемы.

Рассмотрим на отрезке [a; b] обыкновенное дифференциальное уравнение

F(x, y, y ^/,...,y ^(k)) = 0

с граничными условиями вида

f(a, y(a), y ^/(a),...,y ^(k)(a)) = A.

Если граничные условия, т.е. значения функции и ее производных, заданы в одной точке, то говорят, что имеется задача Коши, если в двух – краевая задача. Обыкновенные уравнения делятся на линейные и нелинейные. В случае линейной задачи и само уравнение, и граничные условия являются линейными функциями относительно y, y ^/, ..., y ^(k). В случае нелинейной задачи, по крайней мере, одна из функций F или f является нелинейной.

Для дифференциального уравнения 1-го порядка теоретически можно получить точное аналитическое решение. Однако во многих случаях это сделать тяжело, а для уравнений высших порядков зачастую и невозможно. В связи с этим приходится применять численные методы решения дифференциальных уравнений. Численное решение дифференциального уравнения заключается в переходе от бесконечномерного пространства функций на отрезке [a; b] к конечномерному пространству (дискретизации) и нахождению в нем приближенного решения задачи. Этот процесс состоит из 5 этапов:

1. Выбор конечномерного пространства, в качестве которого может быть выбрано: пространство многочленов степени не выше m; пространство кусочно-постоянных функций; пространство функций на конечном множестве точек; пространство сплайнов и др.

2. Постановка задачи, эквивалентной исходной для выбранного конечномерного пространства. Рассмотрим пример.

Пусть решаемое дифференциальное уравнение имеет вид: y^/ = f₀(x) + f₁(x)∙y; y(a) = y₀. Предположим, что в качестве пространства дискретизации выбрано пространство многочленов степени не выше m, а f₀ и f₁, в свою очередь, являются многочленами степени не выше k. Тогда, полагая , получим

.

Приравняем коэффициенты при одинаковых степенях и приведем подобные. Получим систему уравнений относительно коэффициентов a₀, a₁, ..., a_m. В результате дискретизации задача сводится к решению системы алгебраических уравнений. Различные дискретизации отличаются друг от друга первыми двумя этапами.

3. Решение полученной алгебраической задачи.

4. Восстановление приближенного решения по найденным значениям.

5. Оценка погрешности между приближенным и точным решениями.

На практике нахождение решения дифференциального уравнения обычно сводится к нахождению значений неизвестной функции y в конечном множестве точек.

Пусть на отрезке [a; b] задана задача Коши: , y(a) = y₀. Рассмотрим разбиение отрезка [a; b] точками x_i с постоянным шагом h = (b – a )/n, т.е. x _i = a + ih, где i = 0, 1, …, n. Будем искать значения функции в этих точках. В качестве значения производной функции в точке можно взять одну из формул численного дифференцирования:

– (явная замкнутая схема);

– (неявная замкнутая схема);

– (неявная незамкнутая схема).

Возникающие системы уравнений называются разностными схемами для задачи Коши. Явная схема позволяет, зная у₀, последовательно найти значения функции в остальных точках. В замкнутых схемах количество уравнений совпадают с количеством неизвестных. В незамкнутой схеме уравнений n – 1, а неизвестных – n. Способ, которым незамкнутая схема будет замкнута, повлияет на найденное решение.

Методы решения линейных и нелинейных граничных задач можно разделить на два класса в зависимости от того, является ли процедура решения итерационной или нет.

I. Итерационные методы:

1) методы пристрелки (метод Ньютона, метод параллельной пристрелки и метод квазилинеаризации);

2) конечно-разностные методы (Эйлера, Адамса, Рунге–Кутта);

3) метод интегральных уравнений.

II. Неитерационные методы:

1) суперпозиции;

2) прогонки;

3) сопряженного оператора;

4) преобразования;

5) дифференцирования по параметру;

6) инвариантного погружения.

Одними из наиболее широко используемых методов решения граничных задач является конечно-разностные ме­тоды. Эти методы заключается в переходе от системы обыкновенных дифференциальных уравнений к конечной системе алгебраических уравнений путем замены производных зависимых переменных их конечно-разностным представлением и дальнейшем решении полученных алгебраических уравнений; при этом полу­чается приближенное решение задачи в узловых точках. Для линейных граничных задач соответствующие алгебраические урав­нения также линейны, и решение можно найти за один шаг. При решении нелинейных граничных задач требуются итерации, так как теперь задача должна быть линеаризована. Одним из распространенных методов является линеаризация дифференциаль­ного уравнения при помощи методов квазилинеаризации до замены производных их конечно-разностным представлением. В другом подходе производные предварительно заменяются их конечно-раз­ностным представлением, а затем полученные нелинейные алге­браические уравнения линеаризуются методом Ньютона.

В методе пристрелки, при решении граничной задачи, сначала выбирается не­которое значение для недостающего начального условия. Полу­чающуюся при этом задачу Коши можно решить одним из конечно-разностных методов. Правильность выбранного началь­ного условия проверяется в конечной точке сравнением заданного граничного условия с полученным в результате решения задачи Коши. Если эти граничные условия не совпадают, то для недо­стающего начального условия выбирается новое значение, про­цедура повторяется сначала и так продолжается до тех пор, пока не будет достигнута удовлетворительная точность. В итерацион­ных методах подобного сорта возникает вопрос о существовании регулярной процедуры выбора недостающего начального условия, обеспечивающую быструю сходимость к решению задачи. Такие методы известны: метод Ньютона, метод параллельной пристрелки, метод квазилинеаризации и др.

В методе интегральных уравнений граничная задача заменяется интегральным уравнением, которое решается с помощью квадра­турных формул.

Способ преобразования линейных граничных задач к задачам Коши методом суперпозиции основывается на принципе суперпози­ции, следуя которому можно свести решение граничной задачи к нахождению решений двух или нескольких задач Коши. Ком­бинация этих решений дает решение исходной задачи.

Менее распространенный метод прогонки. В этом методе недостающие начальные условия находятся на этапе прямой прогонки, который включает в себя построение новой задачи Коши (для параметров) и ее интегриро­вание от начальной точки. После того как недостающие началь­ные условия во второй точке найдены, искомое решение может быть найдено при помощи обратной прогонки исходной системы дифференциальных уравнений из второй точки.

Еще одну простую возможность решения граничных задач дает метод сопряженного оператора. Он основывается на по­нятии сопряженной системы уравнений, матрица коэффициентов которой является транспонированной со знаком минус матрицей коэффициентов исходной системы дифференциальных уравнений. Эта сопряженная система осуществляет связь между граничными условиями исходной задачи в начальной и конечной точках.

Метод дифференцирования по параметру, при помощи которого граничная задача сводится к задаче Коши, применяется для решения граничных задач, которые содержат физический параметр в диф­ференциальном уравнении или в граничных условиях. Исходя из известного решения для соответствующего значения параметра, решения задачи для других значений параметра можно получить интегрированием функции скорости изменения решения относи­тельно этого параметра. Для решения на каждом шаге граничных задач, которые являются линейными, можно применить один из неитерационных методов. От шага к шагу параметр меняется на малую величину, решение получает соот­ветствующее приращение, и таким образом исходная задача мо­жет быть решена в широком диапазоне значений параметра без итераций.