0. 3.2 Математическая модель теплопроводности

Из условия сохранения энергии для бесконечно малого объема следует, что скорость притока теплоты плюс скорость тепловыделения в объеме равна скорости оттока теплоты из объема плюс накопление теплоты в объеме:

,

,

где q₊, q_–, q_V, q_x – тепловой поток соответственно входящий, исходящий и выделяющийся в объеме и проходящий через поперечное сечение; S и Р – площадь поперечного сечения и периметр соответственно; V – объем; – коэффициент конвективной теплопередачи.

Упрощая это уравнение и используя уравнение теплопроводности Фурье , получаем запись первого уравнения термодинамики в виде

,

где – коэффициент температуропроводности, ;  – коэффициент теплопроводности.

Граничными условиями могут являться следующие условия:

• температура стенки равна температуре окружающей среды – Т = T_s;

• тепловой поток через границу постоянен – ;

• перенос теплоты на границе обусловлен конвекцией – ;

• перенос теплоты на границе обусловлен излучением – .

В качестве примера рассмотрим задачу по расчету температурных полей опоры теплообменника. Массивный теплообменник прямоугольной формы опирается на одну неподвижную и две подвижные опоры, каждая из опор (см. рис. 3.3) представляет собой стальную пластину размерами 5×0,5×0,03 м (высота опоры 0,5 м, толщина 30 мм). Рабочая температура корпуса теплообменника составляет 530 С, теплообменник теплоизолирован, верхние 150 мм опоры находятся внутри теплоизоляции теплообменника. Теплообменник установлен на бетоном основании. Из условий прочности температура бетона должна быть меньше 90 С. Необходимо определить температуру конца опоры.

Данная задача решается по одномерной расчетной схеме с двумя расчетными участками. Уравнение теплопроводности и граничные условия для участка внутри теплоизоляции (0 < x < l₁) запишем в виде

, Т(0) = 530, ,

для участка вне теплоизоляции (l₁ < x < l₂) –

, ,

где l₁ = 0,15 м; l₂ = 0,5 м; Т_ = 30 С; = 13,4; = 10 Вт/м²/С; Р = 10,06 м; S = 0,15 м²;  = 50 Вт/м/С.

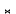
Рис. 3.3. Схематическое изображение опоры

Эта задача решается методом прогонки, изложенным в п. 4.5. Результат расчета представлен в виде графика на рис. 3.4.

Рис. 3.4. Распределение температур в опоре

3. . Математическая модель гидродинамики

В гидродинамике различают три типа задач: внешние, внутренние и струйные. К внешним задачам гидродинамики относят задачи исследования обтекания тел потоком жидкости и газа. Внут­ренние задачи связаны с изучением движения жидкости и газа в каналах и соплах. К струйным относят задачи, в которых изучают движе­ние жидкости и газа в струях, вытекающих из сопл, или в следах за телом. Важными задачами гидродинамики являются задачи о взры­ве, связанные с движением детонационных или ударных волн в различных средах. Рассматривается движение идеальной жидкости, движение сжимаемой жидкости (газа) и движение вязкой жидкости (реальной). Наиболее полно описаны движения идеальной и сжимаемой жидкостей.

Стационарное одномерное течение идеальной жидкости. Для идеальной жидкости (в частности, воду во многих случаях можно считать идеальной жидкостью) одномер­ное стационарное течение можно описать, ис­пользуя уравнения сохранения массы и энергии

и ,

где u – скорость движения жидкости. Решив эти дифференциальные уравнения, получим уравнение неразрывности

и уравнение Бернулли

.

Стационарное течение вязкой жидкости. Для вязкой жидкости одномер­ное стационарное течение можно описать, ис­пользуя уравнения сохранения массы

и энергии

,

,

Решив эти дифференциальные уравнения, получим уравнение неразрывности

и уравнение Бернулли

,

где  – коэффициент Кориолиса (принимает значение для турбулентного потока и находится в интервале от 1 до 2 для ламинарного потока); р₁₂ – величина гидравлических потерь, определяется по формулам гидравлического сопротивления;  – коэффициент Дарси.

Стационарное течение невязкой сжимаемой жидкости. Для описания этого течения запишем уравнение неразрывности

и энергии

,

,

Решив эти дифференциальные уравнения, получим уравнение неразрывности

и уравнение Бернулли

,

где k – коэффициент адиабаты.

Нестационарное одномерное течение сжимаемой жидкости (идеального газа). Состояния движущегося газа с известными термодинамиче­скими свойствами определяются заданием скорости, плотности и давления как функций от координат и времени. Для нахождения этих функций используют систему уравнений, которая представ­ляет собой выраженные в дифференциальной форме общие зако­ны сохранения массы, импульса и энергии. Эти уравнения замы­каются термическим и калорическим уравнениями состояния.

Термическим уравнением состояния называют уравнение, связывающее давление с плотностью и температурой, а калори­ческим – уравнение, определяющее зависимость внутренней энергии (энтальпии) от температуры и давления. В большинстве случаев течение газа сопровождается разного рода неравновес­ными процессами, для описания которых уравнения газовой ди­намики дополняются соответствующими кинетическими или релаксационными уравнениями. Кроме того, в уравнения вво­дят дополнительные члены, учитывающие воздействия неравно­весных процессов на газодинамические параметры. Неравновесные процессы весьма разнообразны. Наиболее часто приходится иметь дело с неравновесным возбуждением колебательных степеней свободы, неравновесной диссоциацией и рекомбинацией, нерав­новесным движением жидких или твердых частиц в условиях не­равновесной конденсации или испарения.

Уравнения сохранения массы, им­пульса (количества движения) и энергии, описывающие одномер­ное нестационарное течение идеального сжимаемого газа, ис­пользуя уравнения состояния, соответственно можно записать в следующем виде:

– уравнения сохранения массы;

– уравнения сохранения энергии;

– уравнения сохранения им­пульса,

где u – скорость течения; а – скорость звука, ; k – отношение удельных теплоемкостей (показатель адиабаты).

Из этих уравнений следуют уравнения одномерной акустики, которые описывают распространение плоских звуковых волн:

,

,

где u и а – плотность и скорость звука в невозмущенной сре­де. Представленная система уравнений является модельной при построении многих разностных схем газовой динамики.

Стационарные двумерные течения идеального газа. Урав­нения сохранения массы, импульса и энергии, описывающие дву­мерные стационарные течения идеального газа, могут быть за­писаны в следующем виде:

,

, ,

,

где i = 1, 2; х_i – оси декартовой (в плоском случае) либо цилиндрической (в осесимметричном случае) системы координат; u_i – проекции вектора скорости на оси системы координат; – энтропия;  = 0 (в плоском случае) или  = 1 (в осесимметричном).

В двумерном случае изоэнтропическое и изоэнергетическое течение является потенциальным безвихревым течением. Введем понятие потенциала скорости : , .

При этом урав­нения, описывающие дву­мерные стационарные течения идеального газа, могут быть за­писаны в частных производ­ных относительно одной искомой функции – потенциала скоро­сти:

.

Линеаризованные уравнения. Если предположить, что воз­мущения, вносимые в поступательный поток, движущийся со скоростью u_, малы, т. е. принять, что u₁ = u_ + u₁’, u₂ = u₂’,  = x₁  u_ +₁, и провести линеаризацию уравнения, пренебрегая членами второго порядка малости, получим уравнение для возмущения потенциала скорости ₁. Опуская индекс, запишем уравнение в возмущениях:

,

где М – число Маха, М = u_/с_. В случае несжимаемой жидко­сти М = 0 и уравнение в возмущениях принимает вид:

.

Это уравнение при  = 0 и М < 1 переходит в уравнение Лапласа; при  = 0 и М > 1 – в волновое уравнение; а при  = 1 – в уравнение Дарбу.

Если скорость газа близка к скорости звука и, предполагая, что угол между направ­лением скорости и осью х₁ мал, можно получить следующее уравнение для потенциала возмущенного течения:

.