Способы получения краевых условий:

• Если известны значения производной в граничных точках f^/(a) = f₀^/ и f^/(b) = f_N^/ , то полагаем m₀ = f₀^/ и m_N = f_N^/.

• В качестве значений m₀ и m _N можно выбрать аппроксимацию производной функции f формулами третьего порядка точности:

;

• Если известны f ^//(a) = f₀^// и f^//(b) = f_N^//, то можно приравнять вторые производные сплайна в граничных точках к заданным вторым производным. В результате получим

и .

Конечный вид сплайна зависит от выбранных краевых условий. При этом возможна любая комбинация краевых условий.

Преимущества аппроксимации сплайнами:

1. Если для аппроксимации функции используется интерполяционный многочлен, то для увеличения точности интерполяции надо уменьшить шаг, т.е. увеличить количество точек, но при этом увеличится степень многочлена, с которым уже труднее работать. Сплайн же позволяет, изменяя количество точек, оставлять степень многочлена постоянной.

2. При работе со сплайном можно гарантировать аппроксимацию не только самой функции, но и аппроксимацию производных.

Для любого отрезка [x_i; x_i+1] максимальное отклонение m производной функции от соответствующей производной сплайна имеет вид

,

где ; С – константа, зависящая от функции, но не зависящая от h.

5.2. Решение систем алгебраических линейных уравнений

Рассмотрим решение системы линейных алгебраических уравнений

или в матричной форме ,

где ; ; ; i, j = 0, 1,…, n.

Если определитель матрицы А отличен от нуля, , то система имеет единственное решение. Но вычисление решения системы, как с помощью обратной матрицы, так и способом Крамера нерационально из-за громадного числа операций.

Среди методов решений линейных систем можно выделить прямые и итерационные методы. Прямые методы позволяют найти решение за конечное число операций, а итерационные – в пределе s → ∞, где s – номер итерации. Прямые методы используют для решения сравнительно неболь­ших линейных систем до порядка 10³, итерационные – до по­рядка 10⁶. Для решения линейных уравнений, как правило, при­меняют итерационные методы.

Метод Гаусса. Простейшим прямым методом является метод исключения Гаусса. Метод Гаусса основан на приведении матрицы А к треугольной, у которой все элементы, расположенные ниже главной диагона­ли, равны нулю. Предположим, что (в противном случае перенумеру­ем переменные). Разделив первое уравнение на а₁₁, по­лучим .

Домножая это уравнение последовательно на а_i1 i = 2, …, n и вычитая из i-го уравнения, исключаем x₁ из всех-уравнений, кроме первого. Далее аналогичную процедуру выполняют с полученной системой. В результате исключения неизвестных приходим к системе с тре­угольной матрицей

.

На этом заканчивается прямой ход исключения. Теперь последовательно вычисляем неизвестные начиная с последней строки матрицы.

Метод Гаусса широко используют в случае матрицы А общего вида. Для уравнений со специальными матрицами существуют более экономичные методы.

Итерационные методы. Для решение системы линейных алгебраических уравнений из итерационных методов наиболее часто используются метод простой итера­ции и метод Зейделя. Метод Зейделя более распространен, т.к. его скорость сходимости выше.

Метод Зейделя. Пусть дана система уравнений .

Предположим, что все диагональные элементы матрицы А отличны от нуля: (, ).

Поделим каждое i уравнение на a_ii :

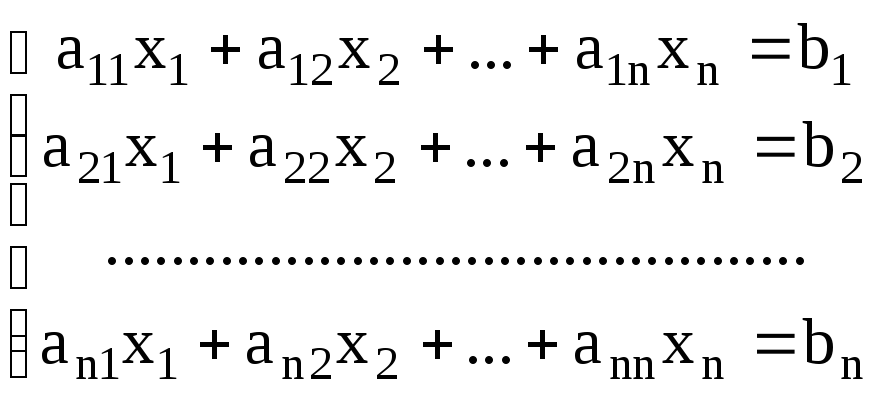
В правой части каждого из уравнений оставим только i–е неизвестные :

,

тогда система запишется в виде

x = Cx + d ,

где , .

Выберем начальное приближение . Каждое следующее приближение вычисляется по следующим формулам :

,

где - i-я компонента k-го приближения.

Данный метод похож на метод простых итераций (), однако скорость сходимости метода Зейделя выше, поскольку в процессе вычислений используются уже найденные компоненты более точного решения.

Для сходимости метода Зейделя достаточно выполнение одного из двух условий :

а) ;

б) матрица А является положительно определенной, т.е. все ее собственные значения больше нуля.