9. Площадь фигуры, ограниченной простым замкнутым контуром с, находится по формуле:

10.2. Примеры решения задач.

Задача 1. Вычислить криволинейный интеграл I-го рода по длине дуги

_{где L- отрезок прямой от т. O(0;0) до B(4;3)}

_{Решение:}

_{Уравнение прямой имеет вид:}

_или

_{Находим тогда}

_{Задача 2. Вычислить площадь фигуры, ограниченной кривыми y = x}²_{, x = y} ² _{и 8xy =1.}

_{Решение:}

Решая совместно уравнения кривых находим координаты точек A и B:

_

_

Значит, _или

_{Это краткое решение. Более подробное решение имеет вид:}

_или

_{1. -дуга параболы y = x}²_{; dy =2xdx; тогда}

2. _{- дуга кривой тогда}

_{3. -дуга кривой тогда}

_{Задача 3. Дано}

_{Проверить, что данное выражение является полным дифференциалом функции «U» и найти эту функцию.}

_{Решение:}

_{- требование полного дифференциала выполняется и данное}

_{выражение можно записать , где U=U(x,y)- искомая функция.}

_{Будем интегрировать dU по ломаной OAM (см. рис.)}

_{y . M (x;y)}

_{O(0;0) A(x;0) x}

_{Учтя, что на пути OA y =0; dy=0 а на пути AM x=const, dx=0, получим:}

_Ответ:

_{Задача 4. Найти центр тяжести дуги полуокружности лежащей в верхней полуплоскости. Плотность считать равной единице.}

_{Решение: Из соображения симметрии ясно, что центр тяжести лежит на оси (OY), поэтому}

_Xc=0.

_{Ордината 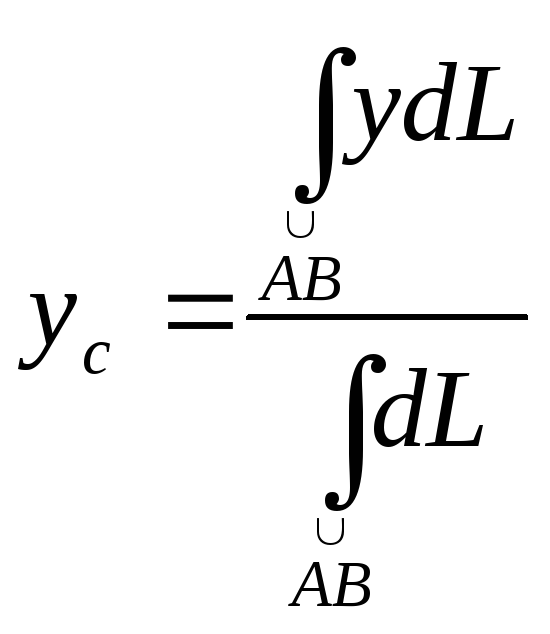, где dL-длина дуги.}

_{- длина полуокружности, т.е}

_Тогда

_Ответ: