В. Несимметричная двойственная пара

Строится, если не выполнено хотя бы одно из условий построения симметричной пары. В этом случае сводим все ограничения задачи к равенствам, применяя дополнительные переменные.

Тогда двойственная задача будет иметь вид:

F = y₁b₁ + y₂ b₂ + …. + y_mb_m → mах;

Замечания. 1. Условия неотрицательности на у_i не накладываются!

2. Если в прямой задаче Z → max, то F → min, а знаки у всех неравенств будут ≥.

Пример 1.7.2. Прямая задача:

Z = 2x₁ – x₂ + x₃ + 5х₄ → max;

3x₁ – 4x₂ + 2x₃ – x₄ ≤ 5;

–2x₁ + x₂ – x₃ + 2x₄ = 6;

2x₁ – x₂ + x₃ – 2x₄ ≥ 1;

x₁ ≥ 0, x₂ ≥ 0; x₃ ≤ 0; x₄ – ?

Приводим задачу к каноническому виду (целевую функцию можно оставить на max), вводя дополнительные переменные: х₃^* = –х₃; х₄ = х₄^* – х₄^**;

Z = 2x₁ – x₂ – x₃^* + 5х₄^* – 5х₄^** → max;

3x₁ – 4x₂ – 2x₃^* – x₄^* + х₄^** + х₅ = 5;

–2x₁ + x₂ + x₃^* + 2x₄^* – 2х₄^** = 6;

2x₁ – x₂ – x₃^* – 2x₄^* + 2х₄^** – х₆ = 1;

x₁ ≥ 0, x₂ ≥ 0; x₃^* ≥ 0; x₄^* ≥ 0; х₄^**≥ 0; х₅ ≥ 0; х₆ ≥ 0.

Строим несимметричную двойственную задачу:

F = 5y₁ + 6y₂ + y₃ → min;

3y₁ – 2y₂ + 2y₃ ≥ 2;

–4y₁ + y₂ – y₃ ≥ –1;

–2y₁ + y₂ – y₃ ≥ 1;

–y₁ + 2y₂ – 2y₃ ≥ 5;

y₁ – 2y₂ + 2y₃ ≥ –5;

y₁ ≥ 0;

–y₃ ≥ 0 ==> y₃ ≤ 0.

Заметим, что 4-е и 5-е ограничения в сумме эквивалентны одному ограничению-равенству: –y₁ + 2y₂ – 2y₃ = 5.

1.8. Основные теоремы двойственности

Достаточно часто можно находить решение двойственной задачи, пользуясь известным решением прямой задачи. Обоснование соответствующих методов дают теоремы двойственности, доказательство которых можно найти в [1]. Сначала сформулируем основную ЛЕММУ в предположении, что в прямой задаче Z → min , а в двойственной F → max.

Значение целевой функции прямой задачи Z(X) при любом допустимом Х не меньше, чем значение целевой функции двойственной задачи F(Y) при любом допустимом Y, т. е. Z(X) ≥ F(Y). Если же для каких-нибудь векторов Х^* и Y^* значения целевых функций совпадают, т. е. Z(Х^*) = F(Y^*), то эти векторы являются оптимальными решениями соответствующих задач.

На основании данной леммы доказывается 1-я основная теорема двойственности. Она включает в себя три утверждения:

1. Если одна из пары двойственных задач обладает оптимальным решением X_опт , то и другая задача обладает оптимальным решением Y_опт , причем Z(X_опт) = F(Y_опт).

2. Если у одной из пары двойственных задач целевая функция не ограничена, то вторая задача не имеет допустимых решений.

3. Если одна из пары двойственных задач не имеет допустимых решений, то вторая задача либо также не имеет допустимых решений, либо имеет неограниченную целевую функцию.

При доказательстве данной теоремы в [1] выводится формула, дающая возможность найти оптимальное решение двойственной задачи, при условии, что прямая задача решена симплекс-методом:

Y_опт = С_б^Т А_б^–1. (1.8.1)

На практике это означает, что из последней симплекс-таблицы (в которой достигнуто условие оптимальности) надо взять вектор-строку С_б^Т и умножить его на матрицу А_б^–1. Эта матрица находится опять-таки в последней симплекс-таблице в столбцах, соответствующих первоначальному базису.

Пример 1.8.1. Рассмотрим применение этого метода на примере задачи, решенной графическим и симплекс-методом (см. п.п. 1.4 и 1.5).

Исходная задача (1.4.2):

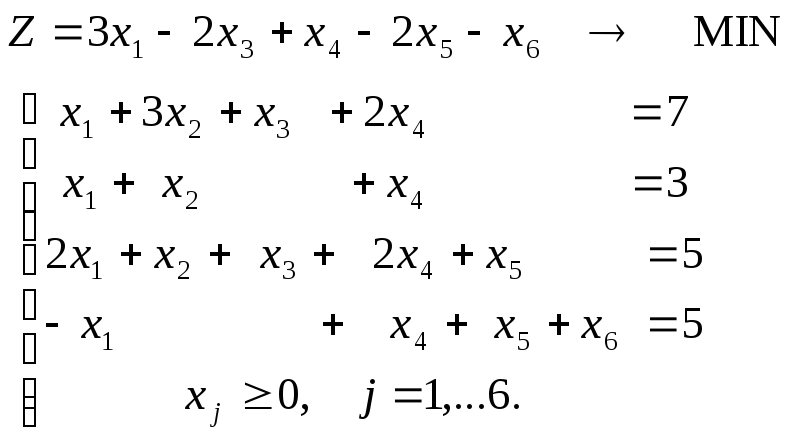
После серии преобразований Жордана-Гаусса она была приведена к виду, на основании которого была построена начальная симплекс-таблица:

Z = 3x₁ – 2x₃ + x₄ – 2x₅ – x₆ → min;

–х₁ + х₂ + х₃ = 1,

х₁ + х₂ + х₄ = 3,

х₁ – 2х₂ + х₅ = 2,

–3х₁ + х₂ + х₆ = 0,

х_j ≥ 0, j = 1, … 6.

Именно по отношению к этой задаче строим несимметричную двойственную по описанным выше правилам. Получаем:

F = y₁ + 3y₂ + 2y₃ → max;

–y₁ + y₂ + y₃ – 3у₄ ≤ 3,

y₁ + y₂ – 2y₃ + y₄ ≤ 0,

y₁ ≤ –2, (1.8.2)

y₂ ≤ 1,

y₃ ≤ –2,

y₄ ≤ –1.

Найдем оптимальное решение этой задачи по формуле (1.8.1). Из последней симплекс-таблицы примера 1.5.1 (п. 1.5.) получаем:

С_б^Т= (3; –1; –2; 0); А_б^–1 = . Тогда умножая вектор-строку на матрицу, получим:

Y_опт = (–5/2; –1/2; –2; –1).

Нетрудно проверить, что компоненты Y_опт удовлетворяют всем ограничениям задачи (1.8.2). Кроме того, F(Y_опт) = –5/2 – 3/2 – 4 = –8 = Z(X_опт), что соответствует 1-ой основной теореме двойственности.

Важную роль в получении и исследовании решений пары двойственных задач играет 2-ая основная теорема двойственности:

Для того, чтобы два допустимых решения двойственной пары Х^*(х₁^*, х₂^*, … х_n^*) и Y^* (y₁^*, y₂^*, … y_m^*) были оптимальны, необходимо и достаточно, чтобы они удовлетворяли так называемым «условиям дополняющей нежесткости»:

т.е. чтобы произведение значения любой переменной из оптимального решения одной задачи на невязку соответствующего ограничения двойственной задачи равнялось нулю.

Приведем примеры практического применения данной теоремы.

Пример 1.8.2. Проверить, является ли вектор Х^* = (12; 4; 0; 0) оптимальным решением следующей задачи линейного программирования:

Z = 8x₁ + 2x₂ – 6x₃ – 5х₄ → max;

x₁ – x₂ – x₃ + x₄ ≤ 10;

4x₁ – 7x₂ – 6x₃ + 3x₄ ≤ 20 ;

x₁ + x₂ + 4x₃ – x₄ ≤ 16;

x_j ≥ 0, j = 1, … 4.

Решение данной задачи состоит из ряда действий.

1. Проверяем Х^* на допустимость, подставляя компоненты в систему ограничений:

12 – 4 – 0 + 0 = 8 < 10;

48 – 28 – 0 + 0 = 20;

12 + 4 + 0 – 0 = 16; x_{1, 2, 3, 4} ≥ 0 – решение допустимо.

2. Находим Z(X^*) = 8*12 + 2*4 = 96 + 8 = 104.

3. Строим двойственную задачу:

F = 10y₁ + 20y₂ + 16y₃ → min;

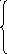y₁ + 4y₂ + y₃ ≥ 8;

–y₁ – 7y₂ + y₃ ≥ 2;

–y₁ – 6y₂ + 4y₃ ≥ –6;

y₁ + 3y₂ – y₃ ≥ –5;

y_1,2,3,4 ≥ 0.

4. Исходя из 2-ой основной теоремы двойственности, заключаем:

– так как первое ограничение исходной задачи для Х^* строгое неравенство, то в Y^* должно быть у₁^* = 0;

– так как х₁^* и х₂^* строго положительны, то 1-е и 2-е ограничения двойственной задачи должны быть равенствами, т. е. верна следующая система алгебраических уравнений:

у₁^* = 0;

у₁^* + 4у₂^* + у₃^* = 8;

–у₁^* – 7у₂^* + у₃^* = 2.

Решая эту систему, находим Y^* = (0; 6/11; 64/11).

5. Проверяем Y^* на допустимость, подставляя эти компоненты в 3-е и 4-е ограничения двойственной задачи (очевидно, условия неотрицательности выполнены):

–36/11 + 256/11 > – 6;

18/11 – 64/11 > – 5, значит решение допустимо.

6. Находим F(Y^*) = 0 + 120/11 + 1024/11 = 1144/11 = 104.

7. Так как F(Y^*) = Z(X^*), то из 1-ой основной теоремы двойственности следует, что Х^* и Y^* являются оптимальными решениями соответствующих задач. Условие примера выполнено.

Замечания

1) Отрицательный ответ при выполнении любого из действий 1, 5 или 7 дает отрицательный ответ и на вопрос исходной задачи.

2) Данный алгоритм наряду с проверкой на оптимальность решения прямой задачи дает (в случае положительного ответа) оптимальное решение двойственной задачи.

Пример 1.8.3. Найти решение задачи линейного программирования путем графического решения соответствующей двойственной задачи:

Z = –x₁ + 2x₂ – 4x₃ + х₄ → min;

4x₁ – x₂ + x₃ – 2x₄ = 2;

–x₁ + 2x₂ + 3x₃ + 4x₄ = 3;

x_j ≥ 0, j = 1, … 4.

Строим несимметричную двойственную задачу:

F = 2y₁ + 3y₂ → max;

4y₁ – y₂ ≤ –1;

–y₁ + 2y₂ ≤ 2

y₁ + 3y₂ ≤ –4;

–2y₁ + 4y₂ ≤ 1.

Так как эта задача имеет только две переменные, ее удобно решить графическим методом.

Очевидно, max F(Y) достигается в точке А, координаты которой находятся из системы уравнений

y₁ + 3y₂ = –4;

4y₁ – y₂ = –1,

т. е. Y^* = (–7/13; –15/13), F(Y^*) = –14/13 – 45/13 = –59/13.

При подстановке компонент Y^* в систему ограничений двойственной задачи мы видим, что 1-е и 3-е ограничения выполняются как равенства, а 2-е и 4-е – как строгие неравенства. Это значит (в соответствии со 2-ой основной теоремой двойственности), что переменные х₂^* и х₄ ^* в оптимальном решении прямой задачи должны равняться нулю. Тогда ограничения прямой задачи превращаются в систему двух уравнений с двумя неизвестными:

4x₁^* + x₃^* = 2;

–x₁^* + 3x₃^* = 3,

решая которую, получаем x₁^* = 3/13; x₃^* = 14/13. Окончательно,

Х^* = (3/13; 0; 14/13; 0), Z(X^*) = 3/13 + 56/13 = 59/13. Так как Z(X^*) = F(Y^*), то по

1-ой основной теореме двойственности X^* и Y^* являются оптимальными решениями пары двойственных задач.

Рассмотрим, наконец, 3-ю основную теорему двойственности, которая служит для исследования вопроса об устойчивости решений задач линейного программирования:

Значения переменных y_i^* в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов ограничений исходной задачи на экстремальное значение ее целевой функции, именно:

.

Практическая сторона данного вопроса раскрывается в следующем важном следствии:

При малых изменениях Δb_i ─ правых частей исходной задачи приращение оптимального значения целевой функции

. (1.8.3)

При более значительных изменениях Δb_i имеет место неравенство:

, (1.8.4)

где – решение двойственной задачи после изменения правых частей исходной.

Пример 1.8.4. Рассмотрим применение 3-ей основной теоремы двойственности к задаче, рассмотренной в примере 1.8.3. Изменим правую часть первого ограничения, добавив единицу к b₁:

Z = –x₁ + 2x₂ – 4x₃ + х₄ → min;

4x₁ – x₂ + x₃ – 2x₄ = 3;

–x₁ + 2x₂ + 3x₃ + 4x₄ = 3;

x_j ≥ 0, j = 1, … 4.

Тогда в двойственной задаче изменится только градиент целевой функции: grad F`= (3; 3), однако, как видно из рис.1.8.1, max F(Y) также будет находиться в точке А (–7/13; –15/13). Решая прямую задачу по 2-ой основной теореме двойственности, для переменных х₁^* и х₃^* получим несколько измененную систему уравнений:

4x₁^* + x₃^* = 3;

–x₁^* + 3x₃^* = 3,

откуда x₁^* = 6/13, x₃^* = 15/13. Окончательно, получаем измененное решение прямой задачи: Х^** = (6/13; 0; 15/13; 0). Ему соответствует новое минимальное значение целевой функции: Z(X^**) = –6/13 – 60/13 = –66/13. Тогда ΔZ = –66/13 – (–59/13) = –7/13. Проверяем равенство (1.8.3):

о тсюда следует, что данные изменения правых частей исходной задачи можно оценить как малые.

Теперь сделаем другие изменения правых частей задачи примера 1.8.3:

Δb = (–2; 0), тогда ограничения приобретут вид:

4x₁ – x₂ + x₃ – 2x₄ = 0;

–x₁ + 2x₂ + 3x₃ + 4x₄ = 3;

x_j ≥ 0, j = 1, … 4.

В результате двойственная целевая функция примет вид: F(Y) = 3у₂ → max.

Следовательно, градиентом целевой функции двойственной задачи будет вектор grad F = (0; 3), и теперь точка максимума изменится (см. рис. 1.8.1):

max F(Y) = F(B). Координаты точки В находим из системы:

y₁ + 3y₂ = –4;

–2y₁ + 4y₂ = 1,

решая которую, получаем: у₁^* = –19/10; у₂^* = –7/10; F(Y^*) = –21/10. Теперь для прямой задачи имеем: x₁^** = 0, x₂^** = 0, а для x₃^** и x₄^** получаем систему:

x₃^** – 2x₄^** = 0;

3x₃^** + 4x₄^** = 3.

Решение системы: x₃^** = 6/10; x₄^** = 3/10. Тогда Х^** = (0; 0; 6/10; 3/10). Z(X^**) = –4*(6/10) + 3/10 = –21/10 = F(Y*). Находим ΔZ = –21/10 – (–59/13) = = 317/130 ≈ 2,44. Проверяем формулы (1.8.3) – (1.8.4):

= –2*(–19/10) = 3,8 ≠ ΔZ, однако = (–7/13)*(–2) ≈ 1,08,

то есть 1,08 ≤ ΔZ ≤ 3,8.

Вывод. Изменения правых частей исходной задачи оказались не малыми (так как в результате этих изменений поменялось решение двойственной задачи).