2.4. Графический метод решения задач нелинейного программирования

Этот метод, как и в случае линейного программирования, применим лишь для задач малой размерности (обычно двумерных). Идея метода: строим область допустимых решений, используя ограничения задачи (в общем случае нелинейные). В отличие от задач линейного программирования область не всегда будет выпуклой и даже односвязной, также экстремум не обязан находиться в крайней точке. Тем не менее, строим, если это возможно, картину линий уровня целевой функции и исследуем тенденции в ее поведении (направления роста и убывания). В результате в ряде случаев удается найти те точки допустимой области, где целевая функция достигает экстремальных значений. Проиллюстрируем сказанное примером.

Пример 2.4.1. Решить графическим методом следующую задачу:

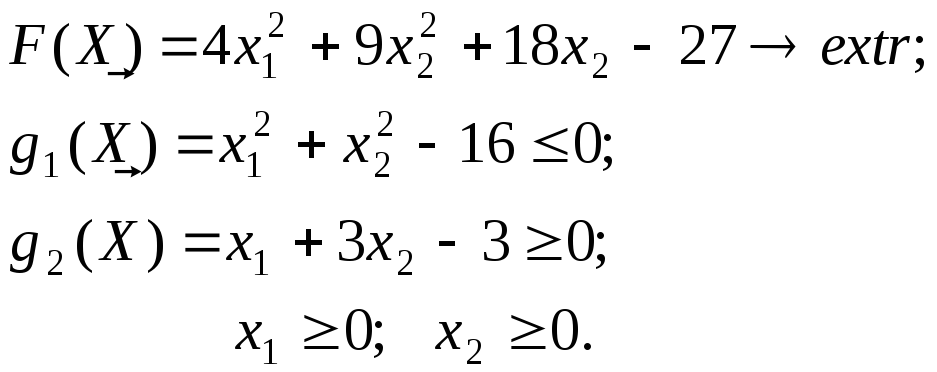
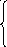
С

Х₂

троим допустимую область, учитывая что ограничение g₂(X) представляет собой внутренность сектора окружности с центром в начале координат и с радиусом 4.

Рис. 2.4.1.

Определим форму линий уровня целевой функции, для чего приравняем ее значение какой-нибудь константе С и проделаем определенные преобразования:

(2.4.1)

Очевидно, что линии уровня представляют собой семейство эллипсов с центром в точке (0; –1), причем при С = 0 длины полуосей a = 3, b = 2. Нанесем несколько этих линий на чертеж.

Легко видеть, что с ростом С длины полуосей увеличиваются, значит максимум целевой функции соответствует «максимальному» эллипсу, имеющему точку соприкосновения с допустимой областью (очевидно, это точка (0; 4)). Вычислим, при каком значении С достигается это касание, для чего подставим в последнее из уравнений (2.4.1) х₁ = 0; х₂ = 4:

Окончательно,

Для решения задачи минимизации той же целевой функции на той же допустимой области надо, очевидно, построить линию уровня, соответствующую минимальному значению С и имеющую общую точку с областью. Из рис. 2.4.1 видно, что это эллипс, касающийся допустимой области на прямой, заданной условием g₂(X) = 0 в точке В. Значение C найдем из условия касания эллипса и прямой, для чего выразим из уравнения g₂(X) = 0 неизвестное х₁ через х₂ и подставим в уравнение линии уровня:

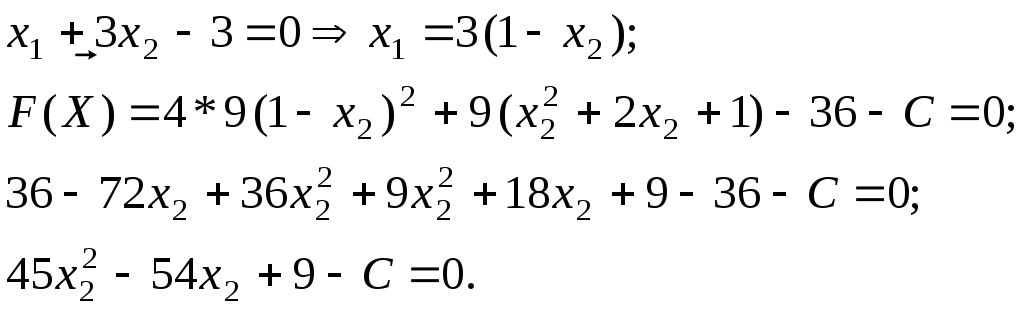
Получили квадратное уравнение относительно х₂. Из соображений касания эллипса и прямой оно должно иметь два равных действительных корня, то есть его дискриминант должен равняться нулю. Из этого условия мы и найдем значение С:

Координаты точки В , а значение целевой функции в этой точке F(B) = F_min = . Задача полностью решена.

2.5. Методы минимизации для задач без ограничений, использующие производные

Общая задача нелинейного программирования без ограничений записывается в виде:

Методы указанного типа приводят поиск к стационарной точке целевой функции, которая определяется уравнением Общая стратегия градиентных методов, которые используют только первые производные целевой функции, сводится к переходу от точки к точке n – мерного евклидова пространства по следующему правилу:

(2.5.1)

где – вектор перехода из точки в точку ;

– единичный вектор в направлении ;

– скаляр (длина шага).

Метод наискорейшего спуска. Идея данного метода принадлежит знаменитому французскому математику О. Коши. Известно, что градиент целевой функции показывает направление ее наибольшего локального возрастания, следовательно, для минимизации этой функции нужно двигаться в противоположном направлении или в направлении антиградиента, которое и считается направлением наискорейшего спуска. Таким образом, получаем:

, (2.5.2)

что после подстановки в (2.5.1) дает:

. (2.5.3)

Поскольку в общем случае один шаг в направлении антиградиента не приводит в точку минимума, формула (2.5.3) должна применяться несколько раз, пока все компоненты градиента целевой функции не обратятся в нуль (стационарная точка). Тип стационарной точки (локальный минимум или седловая точка) проверяется по матрице Гессе (см. 2.2.3). Если не является положительно определенной, то стационарная точка – седловая. В этом случае надо применить какой-нибудь неградиентный метод, чтобы покинуть ее окрестность, а далее снова применять процедуру наискорейшего спуска.

В качестве критерия окончания процесса поиска применяются различные правила, основанные на близости значений на предыдущих шагах либо на малости .

При выборе длины шага λ применяются два основных метода:

а) λ выбирается фиксированной или меняется от шага к шагу.

В этом случае надо тщательно контролировать значение λ, чтобы не «проскочить» поворот к минимуму, т. е. λ надо уменьшать по мере приближения к стационарной точке.

б) λ выбирается из соображений минимизации по λ на соответствующем шаге. В этом случае теоретически доказана сходимость метода наискорейшего спуска за конечное число шагов. Оптимальное значение λ на к-ом шаге получается как решение уравнения:

, (2.5.4)

либо путем одномерной минимизации f(λ) одним из методов п. 2.3.

П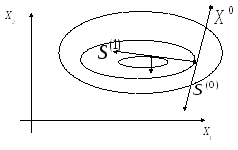 оследний случай имеет простую геометрическую интерпретацию. Известно, что градиент (так же как и антиградиент) всегда перпендикулярен какой-либо линии уровня целевой функции. Предположим, поиск начинается из точки в направлении антиградиента. Тогда длина шага, выбранная из соображений минимизации по λ, обеспечит оптимальное продвижение в сторону минимума до тех пор, пока направление поиска не станет касательным к другой линии уровня. В точке касания делается поворот опять в направлении наискорейшего убывания (т. е. перпендикулярно касательной) и т. д. (рис. 2.5.1).

Рис. 2.5.1

Пример 2.5.1. Найдем методом наискорейшего спуска минимум функции . Вычислим градиент целевой функции: .

А) Сначала предположим, что λ = 1 (фиксированно). Возьмем начальную точку Будем применять формулу (2.5.3), результаты вычислений занесем в таблицу и на рис. 2.5.2:

Шаг	х1	х2				Δх1	Δх2
0	2	2	4	100	≈100	–0,04	–1,00
1	1,96	1,00	3,92	50	50,1	–0,078	–1,00
2	1,88	0	3,76	0	3,76	–1,00	0
3	0,88	0	1,76	0	1,76	–1,00	0
4	–0,12	0	–0,12	0	0,12	1,00	0

Рис. 2.5.2

Легко видеть, что если не изменить длину шага, то поиск будет постоянно «перепрыгивать» из точки (0.88; 0) в точку (-0.12; 0) и минимум (0; 0) никогда не будет найден.

Б) Решим ту же задачу с той же начальной точкой, но длину шага будем находить из формулы (2.5.4).

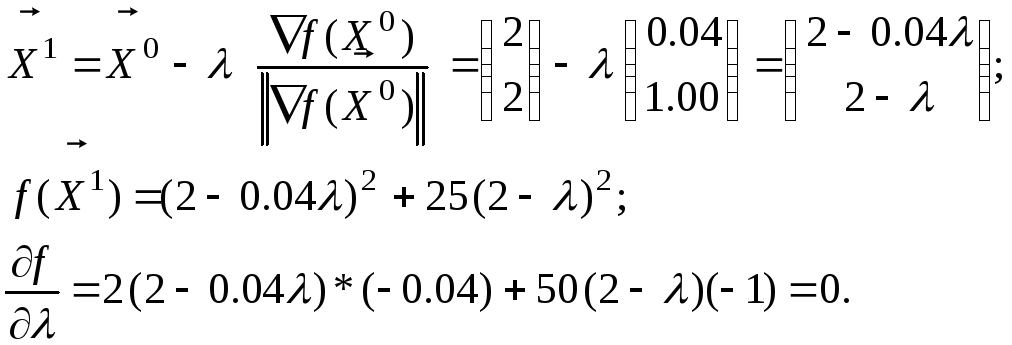
Из этого уравнения находим λ₁ ≈ 2,003, значит .

Продолжаем поиск аналогично и заполняем таблицу:

Шаг (к)	λк	х1	х2			f(X)
0		2	2	4	100	104
1	2,003	1,92	–0,003	3,84	–0,15	3,19
2	1,850	0,070	0,070	0,14	3,50	0,13
3	0,070	0,070	0	0,14	0	0,0049
4	0,5	0	0	0	0	0

Легко видеть, что алгоритм нашел с абсолютной точностью точку минимума.

Если целевая функция слишком сложна или вообще недифференцируема, компоненты ее градиента можно найти по формулам численного дифференцирования. Например, для функции двух переменных имеем:

где δ₁ и δ₂ – малые приращения.

Основной трудностью при использовании метода наискорейшего спуска является зависимость от масштаба переменных. В рассмотренном выше примере коэффициенты при квадратах х₁ и х₂ были различны, в результате линии уровня целевой функции были вытянуты вдоль оси ОХ₁, и образовывали так называемый «овраг». Начальный градиент не был направлен в точку минимума, однако после замены переменных (масштабирования) y = 5x₂ мы получили бы: f(x₁, y) = x₁² + y² и теперь градиент из любой начальной точки направлен в точку минимума (0; 0). Если не применить масштабирование, особенно в случае «овражной» функции большого числа переменных, поиск будет сходиться очень медленно или вообще минимум не будет достигнут за разумное время. В этом случае градиент «перескакивает» с одного склона «оврага» на другой, при этом длина шага постоянно уменьшается. Спасти положение можно или масштабированием или использованием информации второго порядка, т. е. методов вторых производных.

Метод вторых производных (метод Ньютона). Направление поиска в методе наискорейшего спуска можно интерпретировать как результат линейной аппроксимации целевой функции. Методы вторых производных возникли из квадратичной аппроксимации (см. 2.2). Именно, переход от точки к точке осуществляется по правилу:

(2.5.5)

Эта формула получается, если из (2.2.6) находить минимум в направлении , дифференцируя соответствующее векторно-матричное выражение и приравнивая производную к нулю. Направление и длина шага в методе Ньютона определяются автоматически и в случае квадратичной целевой функции минимум достигается за один шаг. В случае произвольной нелинейной функции применяют итерационный процесс, при этом вводится параметр  длина шага λ:

(2.5.6)

Учитывая, что − некий скаляр, формулу (2.5.6) можно переписать в виде:

(2.5.7)

Этот процесс применяют до выполнения критерия окончания (такого же, как в методе наискорейшего спуска). Условиями, гарантирующими сходимость метода Ньютона являются:

1. целевая функция дважды дифференцируема;

2. ее матрица Гессе Н положительно определена.

Обоснование второго требования несложно проделать в случае квадратичной целевой функции. В случае Н > 0 уравнение соответствующей квадратичной формы посредством элементарных преобразований (перенос начала координат и поворот осей) приводится к каноническому уравнению эллипса, т. е. центральной кривой, причем ее центр как раз и соответствует минимуму целевой функции. Если же Н не определена положительно, то соответствующее каноническое уравнение будет иметь гиперболический тип. У этой кривой мнимый центр и это − седловая точка или точка минимакса целевой функции.

Недостатком метода Ньютона можно считать необходимость вычисления аналитически или численно вторых частных производных, что делает алгоритм в некоторых случаях непрактичным.

Пример 2.5.2. Найдем методом Ньютона минимум квадратичной целевой функции:

Найдем градиент и матрицу Гессе:

.

Нетрудно проверить, что Н > 0. Также нетрудно аналитически найти точку минимума: В качестве начальной точки возьмем Найдем определитель матрицы Н и Н^-1: |Н| = 4; .

Применяем формулу (2.5.5):

Действительно, за один шаг мы нашли точку минимума целевой функции.

Метод сопряженных градиентов. Данный метод привлекателен тем, что с его помощью любую квадратичную функцию n переменных можно минимизировать не более чем за n шагов (доказательство можно найти в [3]). Определим сначала понятие сопряженные направления. Система n линейно-независимых направлений поиска называется сопряженной по отношению к некоторой квадратной, положительно определенной матрице Q, если для любых двух направлений верно:

(2.5.8)

В частности, если Q ≡ E, то сопряженность переходит в ортогональность. В рассматриваемом методе (алгоритм разработан американскими математиками Флетчером и Ривсом ) в качестве матрицы Q берется матрица Гессе (гессиан) Н. Алгоритм строится следующим образом:

1. Выбирается начальная точка ; вычисляются начальное значение целевой функции, градиент и гессиан:

2. В качестве начального направления поиска берется направление нормированного антиградиента:

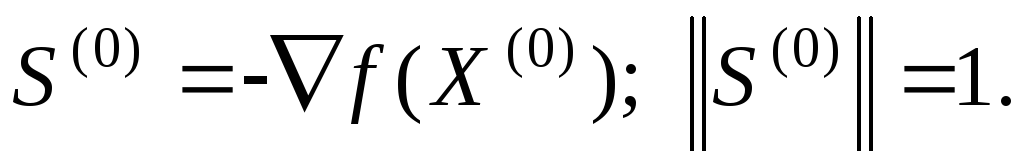
3. Находится первое приближение к минимуму по формуле: 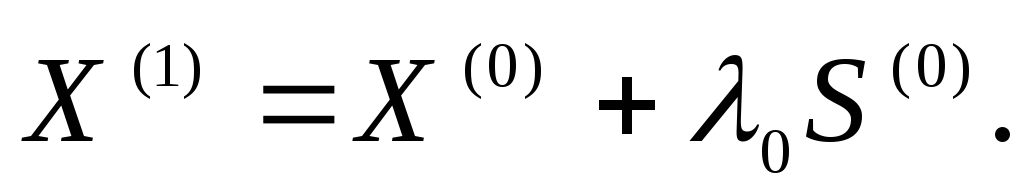При этом параметр λ₀ (длина шага) находится из соотношения, которое является следствием формулы (2.5.4):

(2.5.9)

4. После того, как найдена точка , выбирается следующее направление поиска из соображений нормировки и сопряженности относительно матрицы Н по отношению к направлению и делается шаг в данном направлении из , при этом длина шага вычисляется по формуле, аналогичной (2.5.9):

.

5. Этот процесс продолжается до тех пор, пока не будут сделаны шаги по всем n сопряженным направления (n – количество переменных).

Пример 2.5.3. Решим задачу предыдущего примера методом сопряженных градиентов:

.

В качестве начального направления берем:

.

Применяем (2.5.9):

.

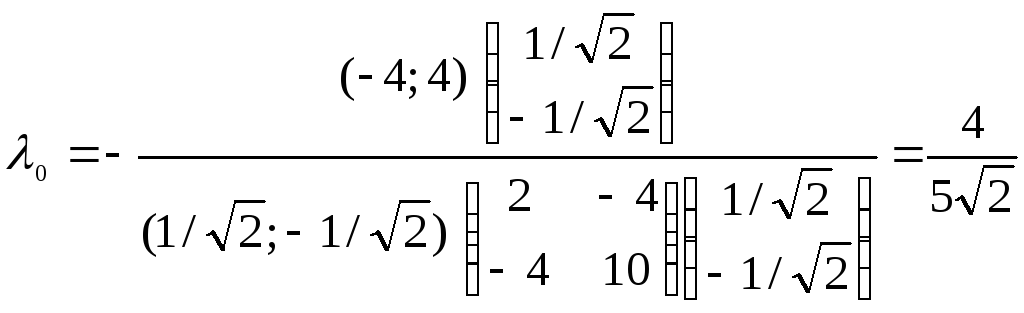Тогда

Находим направление, сопряженное к начальному. Пусть . Тогда верна система уравнений:

Решая ее, получим (можно взять любое из пары решений системы).

Найдем новый градиент: . Пересчитываем длину шага:

Находим следующую точку:

Легко видеть, что мы получили оптимальное решение за 2 шага, что соответствует размерности нашей квадратичной функции.

***

В заключение отметим, что в алгоритме Флетчера – Ривса для задач большой размерности предусмотрена рекуррентная формула нахождения сопряженных направлений поиска: