1.4. Геометрический смысл и графический метод решения задач линейного программирования

Очевидно, множество допустимых решений L задачи ЛП в любой форме записи является выпуклым, как пересечение конечного числа выпуклых множеств. В общем случае оно представляет собой один из следующих объектов:

– плоскость;

– полупространство;

– многогранник (ограниченный или нет);

– многоугольник;

– прямую;

– полупрямую;

– отрезок;

– точку;

– пустое множество.

Целевую функцию задачи ЛП Z можно геометрически интерпретировать как уравнение гиперплоскости в n-мерном пространстве. Придавая Z различные частные значения, мы будем получать различные гиперплоскости или плоскости уровня целевой функции.

В соответствии с теоремой 4 экстремум Z достигается в крайней точке области L, исходя из этого, предлагается следующий графический метод решения задачи ЛП:

Берем произвольную плоскость (в двумерном пространстве – линию) уровня целевой функции Z (как правило, это плоскость Z = 0, или плоскость нулевого уровня). Пользуясь известным свойством градиента функции нескольких переменных, который направлен в сторону возрастания соответствующей функции, будем перемещать плоскость уровня параллельно самой себе в направлении градиента, пока она не достигнет какой-либо крайней точки области L. Очевидно, мы получим точку максимума Z. Наоборот, перемещая плоскость нулевого уровня в направлении антиградиента Z, в соответствующей крайней точке получим минимум Z. Напомним, что в случае линейной целевой функции

.

Кроме того, градиент всегда перпендикулярен линии уровня целевой функции в той точке, в которой он построен. На практике, применяя графический метод, мы можем наблюдать следующие случаи.

Область ограничена, существуют оба экстремума.

О

Рис. 1.4.1

бласть ограничена, минимум достигается в двух крайних точках А и В, следовательно, и на всем отрезке АВ: , 0    1 (рис.1.4.2).

Рис. 1.4.2

Если L не ограничена, то один из экстремумов Z может не достигаться, однако наличие условий неотрицательности на переменные гарантирует наличие второго экстремума (см. рис.1.4.3):

С

Рис. 1.4.3

уществует еще специальный случай:

П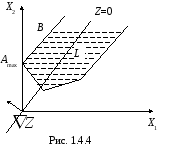 редельное положение разрешающей гиперплоскости совпадает с бесконечным ребром неограниченной области L (рис. 1.4.4). Известна одна крайняя точка А. В этом случае аналитически находят координаты какой-нибудь другой точки В, лежащей на этом же ребре, и записывают решение задачи в виде:

, 0   < . (1.4.1)

Существенным недостатком графического метода является его ограниченная применимость. Он удобен при размерности n = 2 (иногда n = 3), а при большей размерности его можно использовать только в единственном случае:

Пусть задача содержит только ограничения-равенства в количестве m, причем разность n – m (количество степеней свободы задачи) не больше трех. В этом случае из матрицы А системы ограничений методом Жордана – Гаусса выделяются m базисных переменных, которые выражаются через n – m свободных. Затем применяются ограничения x_j  0, j = 1, 2, …, n, которые дают возможность построить область допустимых решений для свободных переменных в пространстве размерности не более 3. В целевой функции все базисные переменные также выражаются через свободные и находится оптимальное решение графическим методом в пространстве n – m измерений. Затем координаты оптимальной точки подставляются в выражения для базисных переменных и получают решение полной n-мерной задачи.

Пример 1.4.1. Решить графическим методом следующую задачу линейного программирования:

(1.4.2)

Решение. Выпишем матрицу системы ограничений и преобразуем ее методом полного исключения (выделены ведущие элементы):

Таблица 1.4.1

1	3	1	2	0	0	7
1	1	0	1	0	0	3
2	1	1	2	1	0	9
–1	0	0	1	1	1	5
–1	1	1	0	0	0	1
1	1	0	1	0	0	3
0	–1	1	0	1	0	3
–2	–1	0	0	1	1	2
–1	1	1	0	0	0	1
1	1	0	1	0	0	3
1	–2	0	0	1	0	2
–2	–1	0	0	1	1	2
–1	1	1	0	0	0	1
1	1	0	1	0	0	3
1	–2	0	0	1	0	2
–3	1	0	0	0	1	0

В результате x₃, x₄, x₅, x₆ оказались базисными переменными, а x₁, x₂ – свободными. Выражаем базисные переменные через свободные и из условий неотрицательности задачи (1.4.2) получаем:

(1.4.3)

Преобразуем целевую функцию:

. Теперь строим на плоскости (x₁0x₂) множество точек, удовлетворяющих системе ограничений (1.4.3):

Очевидно, градиент Z = (–1, –2), поэтому минимум достигается в точке А, которая лежит на пересечении прямых, соответствующих 1-му и 2-му ограничениям из (1.4.3):

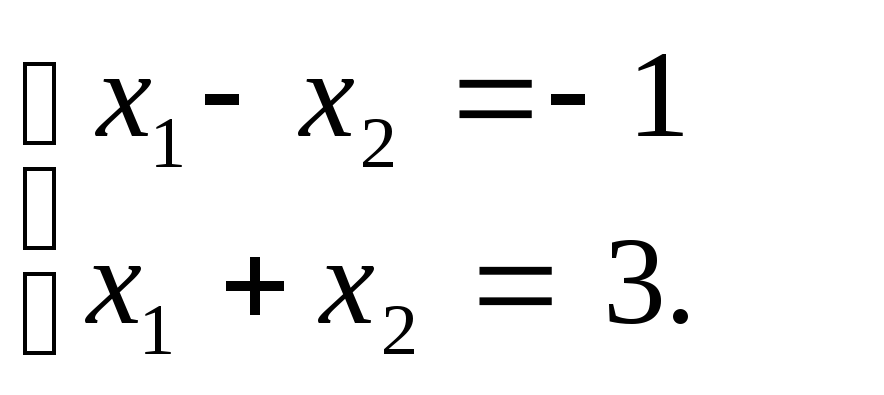Отсюда А = (1; 2).

Из условий (1.4.2) находим оптимальные значения остальных переменных: x₃ = 0; x₄ = 0; x₅ = 5; x₆ = 1. Окончательно: Х_min = (1; 2; 0; 0; 5; 1). Минимальное значение Z равно: Задача полностью решена.