2.7.2. Понятие о методах штрафных функций

Эти методы применяются в различных вариантах, однако их объединяет общая идея: задача нелинейного программирования с ограничениями преобразуется в эквивалентную задачу без ограничений (либо в последовательность таких эквивалентных задач). Это достигается путем введения в целевую функцию так называемой «штрафной добавки» или «штрафа» т. е. величины не дающей достичь минимума, если очередная точка поиска выходит за границу допустимой области. Проиллюстрируем сказанное примером.

Пример 2.7.2. Рассмотрим следующую задачу:

Е е нетрудно решить, выразив из ограничения h х₂ через х₁: х₂ = 4 – х₁, затем подставив в f:

Попробуем теперь рассмотреть штрафную функцию вида:

Решение этой системы: . Очевидно, , тем не менее нельзя считать приемлемым решением исходной задачи, т. к.

Для более точного построения штрафной функции надо присвоить надлежащие веса целевой функции и ограничениям. В дальнейшем максимальный оптимизирующий эффект будет достигаться за счет постоянного компромисса между необходимостью минимизировать функцию и удовлетворить ограничениям.

Введем пока неизвестный весовой множитель λ в «штрафную добавку»:

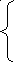
Нетрудно заметить, что при т. е. для корректного построения штрафной функции надо ввести бесконечно большой вес в штрафную добавку.

Обычно, все методы штрафных функций делятся на 2 класса:

1. Параметрические.

2. Непараметрические.

В свою очередь, параметрические методы делятся на 3 категории:

а) Методы внутренней точки: текущая точка поиска «удерживается» внутри допустимой области;

б) Методы внешней точки: генерируется последовательность точек, которые выходят за пределы области, но дают в пределе допустимое решение;

в) Комбинированные, которые особенно хороши, когда ограничения имеют вид равенств. В ходе минимизации некоторые ограничения удовлетворяются, некоторые – нет, однако при достижении оптимального решения все условия в пределах заданного допуска оказываются выполненными.

Формально преобразование задачи (2.7.1) в задачу без ограничений осуществляется так:

(2.7.2)

называется штрафной функцией, а числа λ_i – весовыми коэффициентами, G и H – функционалы над множествами функций g_i и h_i, которые выбираются с учетом ряда требований.

Для G: 1) при что соответствует методам внутренней точки. Пример:

2) при , что соответствует методам внешней точки. Пример:

3)

что соответствует комбинированным методам. Пример:, где u_i – оператор Хэвисайда:

Для H:

Обычно полагают

При любом выборе функционалов H и G должны выполняться требования:

(имеется в виду, что значения λ_i могут меняться от итерации к итерации).

Суть данных требований : влияние «штрафных добавок» на значение Р по мере продвижения процесса оптимизации ослабевает, в результате чего минимум штрафной функции совпадает с минимум исходной целевой функции.