Условия (1) и (2), а также

3), т. е. матрица Гессе положительно определена в точке .

В. Задачи с ограничениями в виде равенств и неравенств (см.(2.2.1))

Если функции дважды дифференцируемы в точке , то необходимыми условиями наличия в точке минимума задачи (2.2.1) являются существование векторов (множителей Лагранжа), для которых

где

–

Достаточные условия – это необходимые условия плюс следующее:

детерминант матрицы Якоби для функций не обращается в нуль в точке .

Наконец, остановимся на классификации методов решения задач нелинейного программирования. Для решения общей задачи НЛП предложено немало алгоритмов, каждый из которых имеет свою сферу применимости. Выбор того или иного метода определяется конкретным содержанием задачи и опытом вычислителя. Классификация методов ведется, в основном, по двум аспектам.

1. По постановке задачи.

   1. По допустимой области:

а) задачи без ограничений;

б) задачи с ограничениями-равенствами;

в) задачи с ограничениями-неравенствами;

г) задачи с ограничениями обеих типов.

2. По характеру переменных:

а) дискретные (целочисленные);

б) непрерывные.

2. По характерным чертам алгоритмов.

2.1. Детерминированный поиск:

а) методы, использующие производные (здесь можно отдельно выделить методы, использующие первые или вторые производные, аналитические производные или численное дифференцирование);

б) методы, не использующие производные (делятся на одновременные или релаксационные);

2.2. Случайный поиск.

В дальнейшем (п. 2.5) мы начнем обзор методов с простейшей классической ситуации – методы, использующие производные для задач без ограничений.

2.3. Эффективные методы одномерной минимизации

Как правило, любой алгоритм численного нахождения минимума функции нескольких переменных включает в себя процедуру одномерной минимизации, т. е. нахождения минимума функции одной переменной. При решении практических задач в силу особенностей целевой функции (например, негладкости или разрывности) классические методы нахождения минимума, связанные с дифференцированием, могут оказаться неприменимы. В силу этого обстоятельства серьёзное внимание уделяется разработке приближенных методов, некоторые из которых мы рассмотрим ниже.

Общая идея многих приближенных методов – в предположении, что функция одной переменной f(x) унимодальна на интервале [a; b], выделить из него достаточно малый отрезок, содержащий точку минимума х^* (будем его называть первичным интервалом неопределенности), а затем, пользуясь той или иной процедурой, «стягивать» этот отрезок вокруг х^* пока не будет достигнута заданная точность. Для нахождения первичного интервала неопределенности можно предложить следующую процедуру, описанную в [3]: на интервале [a; b] выбираем точку х₀ и вычисляем f(x₀). Выбираем шаг Δх и вычисляем f(x₀+Δх). Если f(x₀+Δх) < f(x₀), то направление убывания функции найдено, в противном случае переходим в точку x₀ – Δх, причем f(x₀ – Δх) < f(x₀) в силу унимодальности f(x). Теперь двигаемся в направлении убывания f(х) с удвоенными шагами до тех пор, пока на каком-то шаге значение функции не увеличится. Делим последний шаг пополам и перемещаемся с уменьшенным шагом один раз в противоположном направлении (см. рис. 2.3.1).

Из рисунка видно, что из начальной точки х₀ сделан переход с шагом Δх в точку х₁, и, т. к. f(x₁) < f(x₀), с шагом 2Δх переходим в точку х₂. Опять f(x₂) < f(x₁), следовательно, с шагом 4Δх переходим в точку х₃. Теперь уже f(x₃) > f(x₂), и мы должны с уменьшенным вдвое шагом (т. е. 2Δх) вернуться назад – в точку х₄. Очевидно, за первичный интервал неопределенности следует выбрать интервал [x₂; x₄; x₃], т. к. на концах этого интервала значения минимизируемой функции больше, чем в его середине.

В дальнейшем для обоснования алгоритмов уменьшения первичного интервала неопределенности нам будет полезна следующая

ОСНОВНАЯ ЛЕММА: Пусть функция f(x) унимодальна на интервале [a; b], х₁ и х₂ лежат на [a; b], причем х₁ < х₂. Тогда, если f(x₁) ≤ f(x₂), то точка минимума х^* лежит на [a; x₂], если же f(x₁) ≥ f(x₂), то х^* лежит на [х₁; b].

Данная лемма иллюстрируется рис. 2.3.2:

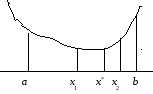
Рис. 2.3.2

Теперь рассмотрим некоторые конкретные алгоритмы.

Алгоритм пассивного поиска. Делим интервал [a; b] = ∆₀ на n равных частей точками {х₀ = a, x₁, …, x_n-1, x_n = b} и в каждой из точек деления находим значение функции f(x_j). Пусть минимальное значение функции достигается в точке x_к. Тогда в силу основной леммы точка минимума должна лежать на интервале [x_k-1; x_k+1] = ∆₁ и этот интервал принимается за новый интервал неопределенности. Снова делим его на n равных частей и продолжаем описанную процедуру до тех пор, пока после s шагов ∆_s не станет меньше заданной точности: ∆_s < ε. В этот момент поиск прекращается и за х^* принимается середина ∆_s.

Метод дихотомии (половинного деления). Пусть минимум функции локализован на интервале [a; b] = ∆₀. Выберем малую положительную величину δ и найдем значения f(x) в точках :

Теперь, в силу Основной леммы, в качестве следующего интервала неопределенности ∆₁ следует выбрать (в зависимости от соотношения значений f(x) в точках а, b, x₁, x₂) либо интервал [a; x₂], либо [x₁; b]. Очевидно, длина ∆₁ равна 0,5(b – a) + δ. Затем вычисляем f(x) в точках х₃ и х₄, отстоящих на δ от середины ∆₁ и продолжаем описанный процесс уменьшения интервала неопределенности. Нетрудно вычислить, что после к-го деления длина ∆_к будет равна: . При выполнении условия |Δ_к| < ε точка минимума х^* определяется как в методе пассивного поиска.

Метод Фибоначчи. Определим последовательность чисел Фибоначчи следующим образом:

F₀ = F₁ = 1; F_i+1 = F_i-1 + F_i; i = 1, 2, …,

т. е. F₂ = 2, F₃ = 3, F₄ = 5 и т. д. Можно вывести общую формулу:

.

Опишем метод Фибоначчи для интервала [0; 1], т. к. любой отрезок [a; b] линейной заменой переменных можно отобразить в отрезок [0; 1]:

. Зададим целое число n и возьмем на интервале [0; 1] две точки: Очевидно, при любом n эти точки будут лежать на [0; 1] симметрично относительно середины отрезка. Действительно, (по определению).

0 ξ₁ ξ₂ 1

Вычислим значения функции в точках ξ₁ и ξ₂. Теперь, в силу Основной леммы, в качестве следующего интервала неопределенности ∆₁ следует выбрать (в зависимости от соотношения значений f(x) в точках 0, 1, ξ₁ и ξ₂) либо интервал [0; ξ₂], либо [ξ₁; 1]. Далее нам достаточно вычислить координату еще одной точки:

(2.3.1)

В первом случае точка ξ₃ будет лежать на этом интервале симметрично к точке ξ₁ относительно его середины, во втором случае – симметрично к точке ξ₂. Продолжая уменьшать интервал неопределенности подобным образом мы после (n–1)-го шага получим точку в середине отрезка локализации экстремума. Длина последнего интервала будет равна . Отсюда следует, что номер максимального числа Фибоначчи (n) следует выбирать по точности ε из неравенства .

Пример 2.3.1. Применим метод Фибоначчи для минимизации функции Понятно, что искомый минимум равен нулю и находится в точке х^* = 1,5. Предварительно найдем Δ₀в соответствии с описанным выше алгоритмом. Возьмем х₀ = 0, Δ_х = 1, тогда х₁ = 1. Очевидно, f(x₀) = 9; f(x₁) = 0,5. Функция уменьшилась, следовательно Δ_х = 2 и х₂ = 3. f(x₂) = 0,9 (функция увеличилась, значит Δ_х делим пополам), и х₃ = 2, f(x₃) = 0,2. Значит, за Δ₀ принимаем отрезок [1; 3], т. к. значения функции на его концах больше, чем в середине. Сделаем теперь замену переменных, отображающую отрезок [1; 3] в отрезок [0; 1]: Соответственно, х = 2ξ + 1. Подставим в целевую функцию и получим: Эту функцию и будем минимизировать на интервале [0; 1]. Выберем точность ε = 0,05 и по ней из неравенства F_n > 1/ε = 20 найдем n = 7, т. к. F₇ = 21. Теперь в соответствии с алгоритмом находим:

. Очевидно, в качестве Δ₁ следует взять отрезок . Находим Следующий интервал неопределенности – Δ₂ = . Находим на нем точку Новый интервал: Δ₃=. Теперь исходя из формулы (2.3.1) мы должны вычислить Очевидно, . Берем на этом интервале точку Последним интервалом неопределенности будет Δ₅ = , и его середина ξ^* = может быть принята за приближенное решение задачи. Возвращаемся к переменной х и получаем: Заметим, что требуемая точность достигнута: │х^* – 1,5│ < 0,05.

Метод «золотого сечения». Термин «золотое сечение» появился еще в античной Греции и подразумевал идеальное с точки зрения художественной эстетики деление отрезка на 2 части, такие, что отношение всей длины к большей части равнялось отношению большей части к меньшей

Теперь нетрудно найти координаты точек D₁ и D₂ для интервала [0; 1] из системы уравнений:

Отсюда .

Соответствующий метод одномерной минимизации (применительно к отрезку [0; 1]) организован следующим образом: вычисляем f(0); f(1); f(D₁); f(D₂) и в соответствии с основной леммой берем в качестве следующего интервала неопределенности либо отрезок [0; D₂], либо отрезок [D₁; 1]. Теперь на выбранный отрезок достаточно нанести еще одну точку, которая в совокупности с имеющейся разделит его в пропорции «золотого сечения». В дальнейшем процесс уменьшения интервала неопределенности проводится аналогично, причем после n шагов мы получим:

.

Пример 2.3.2. Будем минимизировать ту же функцию, что и в предыдущем примере начиная с интервала [1; 3], точность ε = 0,1. Делим интервал в пропорции «золотого сечения» и получаем: Имеем: f(0) = 0,5; f(3) = 0,9; f(D₁) = 0,0678; f(D₂) = 0,3611. В соответствии с основной леммой следующим интервалом неопределенности будет [1; D₂] = [1; 2,236]. На него наносим точку D₃ = 1 + (2,236 – 1)  0,382 = 1,4722; f(D₃) = 0,00098. Дальнейшие шаги:

Δ⁽²⁾ = [1; 1,764]; D₄ = 1 + 0,764  0,382 = 1,2918; f(D₄) = 0,065;

Δ⁽³⁾ = [1,2918; 1,764]; D₅ = 1,2918 + (1,764 – 1,2918)  0,618 = 1,5836;

(очевидно, D₅ должна лежать правее D₃); f(D₅) = 0,008;

Δ⁽⁴⁾ = [1,2918; 1,5836]; D₆ = 1,2918 + (1,5836 – 1,2918)  0,382 = 1,4033; f(D₆) = 0,0126;

Δ⁽⁵⁾ = [1,4033; 1,5836]; D₇ = 1,4033 + (1,5836 – 1,4033)  0,618 = 1,5147; f(D₇) = 0,00026;

Δ⁽⁶⁾ = [1,4722; 1,5836]; D₈ = 1,4722 + (1,5836 – 1,4722)  0,618 = 1,5410; f(D₈) = 0,002;

Δ⁽⁶⁾ = [1,4722; 1,5410].

Длина последнего интервала │Δ⁽⁶⁾│ = 0,0688 < 0,1, значит в качестве приближенного решения берем его середину: х^* = 1,5066; f(x^*) = 0,00005.

Методы, основанные на идее интерполяции (экстраполяции)

Рассмотрим два метода, в которых используется квадратичная или кубическая аппроксимация целевой функции.

А). Метод Дэвиса, Свенна и Кэмпи (ДСК). Находим первичный интервал неопределенности методом, описанным в начале параграфа (см. рис. 2.3.1 где таким интервалом является [x₂; x₄; x₃]). Переобозначим эти точки – x_a, х_b, х_с, где х_b – центральная точка, x_a = х_b – Δx; х_с = х_b + Δx, т. е.

x_a  = х_2, х_b = х₄, x_c  = х₃. Теперь проводим квадратичную интерполяцию для нахождения первого приближения к минимуму:

. (2.3.2)

Если х^* и любая из точек х_a, х_b, х_с, в которой f принимает минимальное значение, отличаются меньше, чем на предписанную точность – поиск заканчивается и точкой минимума считается х^*. В противном случае, начиная из точки х^* с уменьшенным Δx, проводится новый поиск первичного интервала неопределенности с нахождением новых точек x_a, х_b, х_с. Далее применяется формула (2.3.2) для вычисления х^** и т. д. до достижения заданной точности.

В). Метод Пауэлла. В этом алгоритме используется аппроксимация более высокого порядка, благодаря чему можно упростить процедуру поиска трех первых точек. Именно:

1. Из начальной точки х₁ делаем шаг х₂ = х₁ + Δx.

2. Вычисляем f(х₁) и f(х₂).

3. Если f(х₂) < f(х₁), находим х₃ = х₁ + 2Δx,

Если f(х₂) > f(х₁), находим х₃ = х₁ − Δx.

4. Вычисляем f(х₃).

5. Находим приближенное значение точки минимума х^* по формуле:

(2.3.3)

6. Как и в алгоритме ДСК, если х^* и любая из точек х₁, х₂, х₃, в которой f принимает минимальное значение, отличаются меньше, чем на предписанную точность – поиск заканчивается и решением задачи считается точка с наименьшим значением целевой функции. В противном случае из множества х₁, х₂, х₃ отбрасываем «худшую» точку, но так, чтобы не «потерять» интервал, содержащий минимум, и заменяем ее на х^*. Переходим к шагу 5.

7. Работа алгоритма продолжается до тех пор, пока не будет достигнута желаемая точность, упомянутая в 6.

На практике наиболее эффективно себя проявила комбинация алгоритмов ДСК и Паулла. Она включает в себя поиск первичного интервала неопределенности и одного вычисления х^* по формуле (2.3.2) более простой, чем (2.3.3). Затем повторяются шаги 5 и 6 метода Пауэлла до достижения заданной точности.

Пример 2.3.3. Рассмотрим применение комбинации алгоритмов ДСК и Паулла к уже решенной выше задаче:

начальный интервал [1; 3], точность ε = 0,1.

Так как первичный интервал неопределенности уже найден, применяем формулу (2.3.2) метода ДСК для нахождения х^* (считаем, что x_a  = 1, х_b = 2, x_c = 3; соответственно f(х_a) = 0,5, f(х_b) = 0,2, f(х_c) = 0,9, Δx = 1.

Теперь переходим к алгоритму Пауэлла. Отбрасываем точку х₃ = 3 с «худшим» значением функции и делаем аппроксимацию на интервале:

Применяем формулу (2.3.3):

Отбрасываем точку х = 2 и переобозначаем полученные точки:

Снова применяем (2.3.3):

Теперь, в соответствии с п. 6. алгоритма, мы не можем отбросить точку х = 1, несмотря на то, что в ней достигается максимальное значение функции, т. к. мы потеряем интервал, содержащий минимум. Отбрасываем точку х = 1,8, т. е. х₁ = 1; х₂ = 1,5801; х₃ = 1,6371. Применяем (2.3.3):

Сейчас мы видим, что требуемая точность достигнута, т. к. │х^**** – 1,5801│= = │1,5411 – 1,5801│ = 0,039 < 0,1, значит х_min = 1,5411, f_min = 0,002.