1.2. Формы записи задач линейного программирования

Задачи линейного программирования (ЛП), возникающие на практике, описываются линейными соотношениями, которые включают в себя:

• целевую функцию,

• ограничения, в общем случае, трех видов: равенств, неравенств со знаком и неравенств со знаком .

Следовательно, в самом общем случае задача линейного программирования имеет вид:

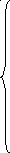(1.2.1)

Рассмотрим два очевидных утверждения, позволяющих упростить (унифицировать) задачу (1.2.1).

Утверждение 1. Задачу максимизации функции Z(X) можно свести к задаче минимизации функции (–Z(Х)), при этом оптимальные решения будут совпадать, т. е.

, где – оптимальное решение.

Утверждение 2. Решение любой линейной системы неравенств и уравнений всегда можно свести к решению системы только линейных уравнений с неотрицательными переменными.

Действительно, мы можем в нашей задаче использовать только неотрицательные переменные, руководствуясь следующими соображениями:

– если на какую-либо переменную наложено условие х_k ≤ 0, то можно ввести новую переменную x_k^’ = –х_k, которая будет неотрицательной;

– если на какую-либо переменную x_s не наложено никаких условий, то ее можно заменить на разность двух неотрицательных переменных:

x_s = x_s^’– x_s^’’, x_s^’ ≥ 0, x_s^’’ ≥ 0 (известный факт из теории чисел: любое вещественное число можно представить в виде разности двух неотрицательных чисел).

Кроме того, все ограничения–неравенства можно заменить равенствами, вводя так называемые дополнительные переменные (неотрицательные переменные, вводимые в левую часть ограничения-неравенства с коэффициентами +1 или –1 с целью приравнять левую и правую части ограничения). В результате применения всех этих операций задача линейного программирования сведется к так называемому каноническому виду:

(1.2.2)

или в векторно-матричной форме:

(1.2.3)

Обычно принимают соглашение, что все правые части b_i  0, в противном случае соответствующее ограничение умножают на (–1). Ограничения из (1.2.3), включающие две и более переменных, называют основными, а ограничения вида x_j  0 – условиями неотрицательности.

Пример 1.2.1. Дана задача:

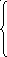
Приведем ее к каноническому виду. Введем новые переменные так, что . Также для превращения неравенств в равенства введем дополнительные переменные x₄ и x₅. Заменим целевую функцию: . Тогда получим задачу в каноническом виде:

Нам понадобится еще так называемая векторная форма записи канонического вида задачи линейного программирования:

(1.2.4)

1.3. Свойства решений задач линейного программирования

Введем некоторые важные определения относительно задачи ЛП, записанной в форме (1.2.4):

1. Допустимым решением (планом) задачи ЛП будем называть вектор , удовлетворяющий всем ограничениям задачи.

2. Допустимое решение называется базисным, если ему соответствует разложение вектора правых частей по линейно-независимым векторам . Поскольку данные вектора имеют m компонент, в базисе {} содержится m векторов, значит в допустимом базисном решении (ДБР) может присутствовать не более m положительных компонент x_j.

3. ДБР называется невырожденным, если оно содержит ровно m положительных компонент.

4. ДБР называется оптимальным решением (планом), если оно доставляет экстремум целевой функции.

5. Компоненты ДБР, соответствующие векторам его базиса, будем называть базисными переменными, остальные – небазисными.

Обозначим через L множество всех допустимых решений и сформулируем относительно него несколько важных теорем, строгое доказательство которых можно найти в [1]:

Теорема 1. Множество L выпукло.

В задачах линейного программирования L представляет собой, как правило, ограниченную или неограниченную многогранную область. Она состоит из внутренних, граничных и крайних (т. е. таких, которые не могут быть представлены в виде выпуклой линейной комбинации внутренних или граничных) точек.

Теорема 2. Множество L содержит в себе конечное число крайних точек.

Теорема 3. Любую точку X ограниченной области L можно представить в виде выпуклой линейной комбинации крайних точек L.

Теорема 4. Целевая функция Z задачи линейного программирования достигает своего экстремума в крайней точке L – области допустимых решений.

Теорема 5. Если Z достигает экстремума одновременно в нескольких крайних точках L, то такое же значение она принимает и в любой точке, являющейся выпуклой линейной комбинацией этих крайних точек.

Теорема 6. Любая крайняя точка L является ДБР соответствующей задачи линейного программирования. Более того, система крайних точек L совпадает с множеством ДБР.

Последняя теорема имеет важное следствие:

С каждой крайней точкой L связано ровно m линейно-независимых векторов из столбцов матрицы А: {} при условии, что rang A = m.

Очевидно, эти m векторов можно выбрать способами, следовательно, это число есть верхняя граница числа ДБР. Напрашивается простейший метод нахождения экстремума – перебор всех решений, однако даже при сравнительно небольших m и n этот метод практически неприменим. Необходим метод упорядоченного перебора ДБР. Таким и является симплекс-метод Дж. Данцига. Он гарантирует получение оптимального решения либо устанавливает неограниченность целевой функции (отсутствие оптимального решения) не более, чем за 2m шагов.