2.1.3. Симплекс-метод в длп

Основные свойства задачи ДЛП – ограничения на переменные линейны и экстремум достигается в крайней точке допустимой области. Они позволяют применить для ее решения симплексный метод. Предварительно нам надо преобразовать нашу задачу в эквивалентную задачу линейного программирования. Рассмотрим неоднородную целевую функцию:

.

Предположим, что нигде в области L знаменатель дроби , более того, (иначе знак « – » можно отнести к числителю). Введем новые переменные у₀, у₁, …у_n по формулам:

(2.1.8)

Тогда исходная задача перепишется так:

Преобразуем ограничения.

Старые ограничения:

(2.1.9)

умножим обе части (2.1.9) на у₀:

Условия неотрицательности х_j ≥ 0 (j = 1, …, n), учитывая, что Z₂(X) ≥ 0, перепишутся в виде: y_j ≥ 0 (j = 1, …, n). Кроме того, учитывая определение у₀, получим еще одно ограничение-равенство:

.

Подытоживая полученные результаты, получим в переменных у_j (j = 0, …, n) эквивалентную задачу линейного программирования:

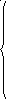(2.1.10)

Данную задачу можно решить обычным симплекс-методом, найти , -затем перейти к , используя формулы . Очевидно, будет равно .

Пример 2.1.2. Решить задачу примера 2.1.1. симплексным методом.

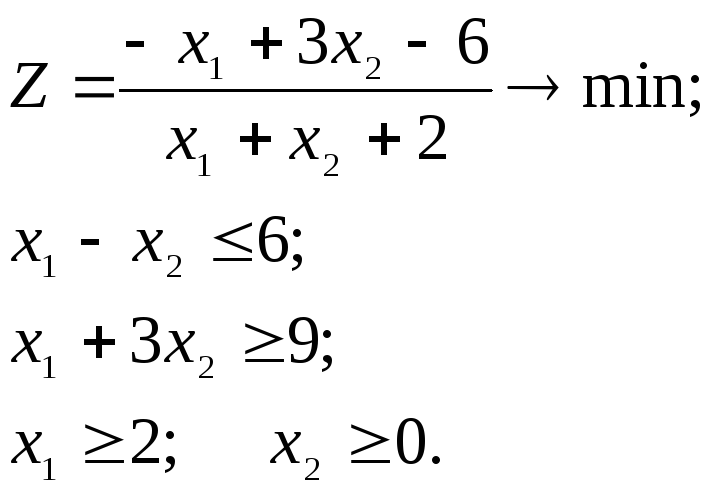
Приведем ограничения задачи к каноническому виду, вводя дополнительные переменные:

Вводим новые переменные у_j и получаем задачу линейного программирования в соответствии с формулами (2.1.10):

Для получения начального базисного решения преобразуем матрицу системы ограничений: 2-е и 3-е уравнения умножим на (-1) и проделаем один шаг метода полного исключения:

-6	1	-1	1	0	0	0
9	-1	-3	0	1	0	0
2	-1	0	0	0	1	0
2	1	1	0	0	0	1
-4	2	0	1	0	0	1
15	2	0	0	1	0	3
2	-1	0	0	0	1	0
2	1	1	0	0	0	1

Заполняем начальную симплекс-таблицу и преобразовываем ее по правилам симплекс-метода до получения оптимального решения:

i	Базис	Сбаз	В	с0= -6	с1= -1	с2 = 3	с3= 0	с4= 0	с5=0	К∑
				А 0	А 1	А 2	А 3	А 4	А 5
1 2 3 4	А3 А 4 А 5 А 2	0 0 0 3	1 3 0 1	-4 15 2 2	2 2 -1 1	0 0 0 1	1 0 0 0	0 1 0 0	0 0 1 0	0 21 2 5
m+1			3	12	4	0	0	0	0
1 2 3 4	А 3 А 4 А 0 А 2	0 0 -6 3	1 3 0 1	0 0 1 0	0 19/2 -1/2 2	0 0 0 1	1 0 0 0	0 1 0 0	2 -15/2 1/2 -1	4 6 1 3
m+1			3	0	10	0	0	0	-6

1 2 3 4	А 3 А 1 А 0 А 2	0 -1 -6 3	1 6/19 3/19 7/19	0 0 1 0	0 1 0 0	0 0 0 1	1 0 0 0	0 2/19 1/19 -4/19	2 -15/19 2/19 11/19	4 12/19 25/19 33/19
m+1			-3/19	0	0	0	0	-20/19	36/19
1 2 3 4	А 5 А 1 А 0 А 2	0 -1 -6 3	1/2 27/38 2/19 3/38	0 0 1 0	0 1 0 0	0 0 0 1	1/2 15/38 -1/19 -11/38	0 2/19 1/19 -4/19	1 0 0 0	2 42/19 21/19 11/19
m+1			-21/199	0	0	0	-18/19	-20/19	0

В последней таблице достигнуто оптимальное решение:

у₀ = 2/19; у₁ = 27/38; у₂ = 3/38; φ(Y_опт) = –21/19.

Переходим к старым переменным по формулам: . Тогда

Легко видеть, что полученное решение полностью совпадает с результатами графического метода.