1.7. Элементы теории двойственности

Во многих естественных науках – физике, химии, математике – часто встречается понятие двойственности: двойственные теоремы, принципы двойственности, двойственные задачи. Рассмотрение этих вопросов часто дает практическую пользу в исследованиях, связанных с соответствующими дисциплинами. В экономике также встречаются подобные понятия. В качестве примера рассмотрим известную задачу производственного планирования (см. 1.1. А). Ее математическая модель имеет вид:

(1.7.1)

Здесь n – количество видов продукции,

m – количество видов ресурсов,

a_ij – расход i-го ресурса на единицу j-го вида продукции;

b_i – запасы ресурсов (i = 1, … m);

c_j – прибыль от реализации j-го вида продукции (j = 1, … n);

– планируемые объемы выпуска каждого вида продукции.

Сформулируем несколько иную экономическую задачу. Пусть предприятие решило продать все свои ресурсы. При этом необходимо установить на них оптимальные цены: y₁, y₂, … y_m, руководствуясь следующими соображениями:

1. покупатель стремится минимизировать общую стоимость ресурсов;

2. предприятие за каждый вид ресурса хочет получить сумму, не меньшую той, которую оно получит, производя из ресурсов продукцию.

Отсюда следует такая математическая модель:

F = y₁b₁ + y₂b₂ + … + y_mb_m → min;

(1.7.2)

Обе модели являются задачами линейного программирования и называются взаимно двойственными или образуют так называемую симметричную двойственную пару задач.

Дадим формальные правила построения двойственных задач.

А. Симметричная двойственная пара

Строится в том случае, когда в исходной (прямой) задаче наложены условия неотрицательности на все переменные, все ограничения имеют вид неравенств одного знака, причем при Z → max знаки неравенств ≤, а при Z → min знаки неравенств ≥. Тогда применяем следующие правила:

1) Если Z → max, то F → min, если Z → min, то F → max.

2) Если в прямой задаче n переменных и m ограничений, то в двойственной будет m переменных и n ограничений.

3) Если А – матрица системы ограничений прямой задачи, то соответствующей матрицей системы ограничений двойственной задачи будет транспонированная матрица А^т.

4) Знаки в ограничениях – неравенствах у прямой и двойственной задач противоположны.

5) Если с_j – коэффициенты целевой функции Z, а b_i – правые части ограничений, то у двойственной задачи с_j будут правыми частями ограничений, а b_i – коэффициентами целевой функции F.

6) Если все х_j ≥ 0, то и все y_i ≥ 0.

Пример 1.7.1. Руководствуясь этими правилами, построим двойственную задачу к следующей задаче линейного программирования:

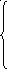Z = 3x₁ + 4x₂ → min;

5x₁ – 2x₂ ≥ 14;

x₁ + x₂ ≤ 9;

–x₁ + 4x₂ ≥ – 4;

x₂ ≤ 6;

x₁ ≥ 0; x₂ ≥ 0.

Здесь пока не выполнены условия построения симметричной двойственной задачи (при Z → min знаки всех неравенств должны быть ≥), но мы имеем право умножить 2-е и 4-е неравенства на (–1) и поменять знаки. Получаем:

Z = 3x₁ + 4x₂ → min;

5x₁ – 2x₂ ≥ 14;

–x₁ – x₂ ≥ – 9;

–x₁ + 4x₂ ≥ – 4;

–x₂ ≥ – 6;

x₁ ≥ 0; x₂ ≥ 0.

Теперь в соответствии с правилами 1) – 6) строим двойственную задачу:

F = 14y₁ – 9y₂ – 4y₃ – 6y₄ → max;

y₁ – y₂ – y₃ ≤ 3;

–2y₁ – y₂ + 4y₃ – y₄ ≤ 4;

y₁ ≥ 0, y₂ ≥ 0, y₃ ≥ 0, y₄ ≥ 0.