Часть 2. Нелинейное программирование

Прежде чем рассмотреть вопросы, связанные с общей постановкой задачи нелинейного программирования, остановимся на одном классе задач, методы решения которых очень близки к методам линейного программирования.

2.1. Дробно-линейное программирование

2.1.1. Постановка задачи

Достаточно часто в оптимизационных задачах приходится находить экстремум дробно-линейной целевой функции вида:

(2.1.1)

Примеры

1. Обозначим через х_j время работы по j-ой технологии, а через c_j и d_j – соответственно производственные затраты и выход продукции в единицу времени. Тогда целевая функция Z будет представлять собой себестоимость продукции и, очевидно, уместно поставить задачу ее минимизации.

2. С другой стороны, определим х_j аналогично, а c_j и d_j – соответственно как чистый доход и затраты в единицу времени. Тогда Z будет представлять собой рентабельность производства и ее надо максимизировать.

Общую задачу дробно-линейного программирования (в дальнейшем длп) обычно записывают в виде:

при ограничениях:

(2.1.2)

Очевидно, что, как и в линейном программировании, ограничения любого другого вида могут быть приведены к форме (2.1.2), возможно с применением дополнительных переменных. Достаточно часто рассматривается и так называемая неоднородная дробно-линейная целевая функция:

(2.1.3)

Окончательно, можно сказать, что задача ДЛП – это задача нахождения экстремума дробно-линейной целевой функции на множестве неотрицательных значений независимых переменных при линейных ограничениях. Исходя из этого, можно утверждать, что, как и в задачах линейного программирования (в дальнейшем – ЛП), область допустимых решений L является выпуклым множеством и содержит конечное число крайних точек. Также сохраняются все основные определения теории ЛП: допустимое решение, базисное решение, оптимальное решение.

Для обоснования методов решения задач ДЛП важную роль играют следующие теоремы:

Теорема 1. Дробно-линейная функция Z является монотонной на любом прямолинейном отрезке, принадлежащем области L.

Теорема 2. Дробно-линейная функция Z достигает своего экстремума в крайней точке области L.

Теорема 3. Если функция Z достигает экстремума одновременно в нескольких крайних точках области L, то это же значение она принимает в любой точке, представимой в виде выпуклой линейной комбинации этих крайних точек.

Доказательство этих теорем приведено в книге [1].

2.1.2. Графическое решение задач длп

Так же как и в ЛП, данный метод применим лишь при небольшой размерности задачи и особенно хорошо он иллюстрируется для n = 2.

Сначала рассмотрим однородную задачу ДЛП:

(2.1.4)

Для применения данного метода существенным является предположение о том, что знаменатель (2.1.4) нигде в области L не обращается в нуль. Рассмотрим какую-нибудь линию уровня функции Z = Z₀:

(2.1.5)

Выразим отсюда х₂ через х₁:

Теперь мы видим, что линии уровня Z представляют собой прямые, проходящие через начало координат и имеющие угловой коэффициент:

.

( см. рис. 2.1.1):

Очевидно, k зависит от Z₀. Выясним характер этой зависимости при помощи исследования производной:

(2.1.6)

Мы видим, что знаменатель дроби положителен, а числитель не зависит от Z₀, следовательно, производная сохраняет постоянный знак в области L, причем этот знак зависит от знака выражения Δ = d₁c₂ – d₂c₁. Именно:

– если Δ > 0, то с ростом Z растет и k, или, что аналогично, с ростом k растет и Z;

– с другой стороны, если Δ < 0, то с ростом k Z уменьшается.

На этих соображениях основан графический метод решения задач ДЛП. Предлагается следующий алгоритм:

1. Вычисляем величину Δ и определяем ее знак.

2. Строим область допустимых решений L и произвольную прямую вида х₂ = kx₁, проходящую через начало координат (линию уровня Z).

3. Если Δ > 0, вращаем построенную прямую вокруг начала координат против часовой стрелки (это соответствует возрастанию k) до соприкосновения с последней крайней точкой области L, в этой точке и будет находиться максимум функции Z.

4. Наоборот, если Δ < 0, вращаем линию уровня вокруг начала координат по часовой стрелке и в последней крайней точке найдем максимум Z.

5. Для нахождения минимума Z действия, описанные в п.п. 3 и 4 производятся «с точностью до наоборот»: при Δ > 0 вращаем линию уровня по часовой стрелке, при Δ < 0 – против.

При этот могут встретиться различные случаи:

Z = Z_min

Z = Z_max

Рис. 2.1.2. L ограничена, min и max достигаются (Δ > 0)

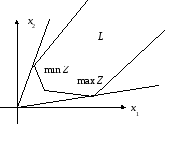
Рис. 2.1.3. Область не ограничена, но

оба экстремума существуют (∆ < 0)

Рис. 2.1.4. Область не ограничена, мах

достигается, min асимптотический

(∆ > 0)

Рис. 2.1.5. Область не ограничена,

оба экстремума асимптотические

(∆ < 0)

Рассмотрим теперь неоднородную задачу ДЛП:

(2.1.7)

Посредством линейной замены переменных преобразуем целевую функцию в однородную. Именно, перенесем начало координат в точку (ξ₁, ξ₂), введя новые переменные y₁ и y₂ по формулам: х₁ = у₁ + ξ₁, х₂ = у₂ + ξ₂. Тогда

Подберем ξ₁ и ξ₂ так, чтобы данная функция стала однородной. Для этого решаем систему уравнений:

Из системы находим координаты нового начала координат М = (ξ₁, ξ₂). Дальнейшие действия аналогичны описанным выше:

1. Вычисляем величину Δ и определяем ее знак.

2. Строим область допустимых решений L и произвольную прямую, проходящую через точку М (линию уровня Z).

3. В зависимости от знака Δ и от необходимого экстремума вращаем эту линию уровня вокруг точки М по тем же правилам, как и в однородном случае.

Замечание: Как и в случае однородной целевой функции проверяем, чтобы ни в одной точке области L знаменатель дроби (2.1.7) не обращался в нуль.

Пример 2.1.1. Рассмотрим следующую задачу ДЛП:

Так как целевая функция неоднородна, находим точку М = (ξ₁, ξ₂), вокруг которой будем вращать линию уровня. Решаем систему уравнений:

Получаем:

Вычисляем Δ = d₁c₂ – d₂c₁ = 1*3 + 1*1 = 4 > 0, значит для нахождения минимума будем вращать разрешающую прямую по часовой стрелке. Строим область L:

Рис. 2.1.6.

Очевидно, вращая линию уровня Z = Z₀ вокруг точки М, мы получим решение задачи на минимум в крайней точке области L – точке A = (27/4; 3/4). Эти координаты мы находим, решив систему из уравнений прямых, пересекающихся в этой точке:

х₁ – х₂ = 6;

х₁ + 3х₂ = 9. Z_min = .