2.2. Общая задача нелинейного программирования. Классификация вычислительных методов
Общую задачу нелинейного программирования (в дальнейшем НЛП) обычно записывают в виде:
(2.2.1)
При
этом подразумевается, что либо
,
либо любая из функций, задающих
ограничения, являются нелинейными.
Приведем определения и терминологию, характерные для задач нелинейного программирования:
Вектор
,
доставляющий экстремум
,
называется оптимальной
точкой, а
соответствующее значение
– оптимальным
значением целевой функции. Пара
,
называется оптимальным
решением.
Целевая
функция называется унимодальной,
если она имеет единственный экстремум,
в противном случае она называется
мультимодальной.
У мультимодальной функции различают
глобальный
(или
абсолютный)
экстремум и локальные
(относительные)
экстремумы. Локальный
минимум
определяется как точка, в достаточно
малой окрестности которой
Для глобального
минимума
это неравенство верно во всей области
D.
Подобным образом (но со знаком неравенства
≥) определяются локальный
и глобальный
максимум.
Функция
называется выпуклой
в области
D,
если для любых двух точек
имеет место неравенство:
(2.2.2)
Если
в (2.2.2) знак неравенства <, то f
называется строго
выпуклой,
соответственно, если это неравенство
выполняется со знаками ≥ (>), то функция
называется вогнутой
(строго вогнутой).
Верны и такие соотношения: если функция
выпукла, то
вогнута и наоборот.
Дифференцируемая выпуклая функция обладает следующими свойствами:
3)
в области выпуклости
имеет только один экстремум.
Здесь мы применили обозначения:
градиент
функции f,
соответственно
–
транспонированный градиент, т. е.
вектор-строка;
– матрица
Гессе функции f
или матрица, составленная из вторых
частных производных:
(2.2.3)
Условие Н ≥ 0 означает неотрицательную определенность матрицы Н.
Из свойства 3) следует, что понятие выпуклости связано с понятием унимодальности, однако является более сильным:
F(х)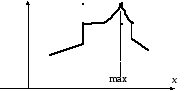
Рис. 2.2.1
На рисунке мы видим график разрывной недифференцируемой функции, которая, тем не менее, является унимодальной.
Определив понятие выпуклой функции, можно сформулировать важный частный случай общей задачи нелинейного программирования – задачу выпуклого программирования:
(2.2.4)
При этом подразумевается, что функция f выпукла, а все функции gi вогнуты, т. е. ограничения образуют выпуклое множество. Исходя из перечисленных выше свойств, можно утверждать: локальный минимум задачи (2.2.4) одновременно является и глобальным. Аналогично, если целевая функция вогнута и ограничения образуют выпуклое множество, то локальный максимум совпадает с глобальным.
Пример 2.2.1. Рассмотрим задачу нелинейного программирования:
+
4 → min;
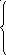
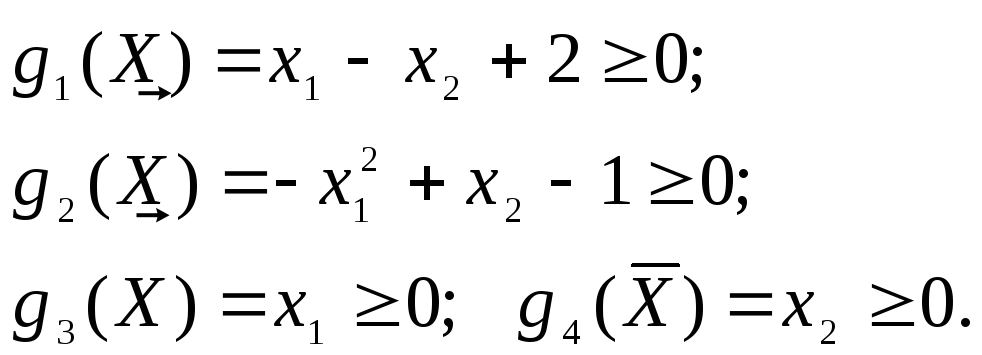
Очевидно,
,
следовательно, линиями уровня целевой
функции будут концентрические окружности
с центром в точке (2; 0).
х1
← допустимая область
Рис. 2.2.2
Очевидно, минимум целевой функции достигается в точке А, в которой «минимальная» линия уровня касается допустимой области. При этом глобальный и локальный минимумы совпадают. Проверим матрицы Гессе:
Значит, f выпукла, а g2 вогнута, g1 – линейная функция, т. е. является одновременно и выпуклой и вогнутой. Таким образом, данная задача относится к задачам выпуклого программирования.
В
данной задаче экстремум достигается
в граничной точке области D.
Такой экстремум будем называть условным
оптимумом.
Соответственно, ограничение-неравенство
,
которое обращается в нуль для точки
экстремума, называется активным
ограничением.
Одним из важнейших типов задач нелинейного программирования являются задачи квадратичного программирования. Их постановка такова:
(2.2.5)
Здесь
Q
– положительно определенная квадратная
симметрическая матрица; А – матрица
коэффициентов левых частей ограничений;
и
– векторы
из констант. Таким образом, задача
квадратичного программирования
– это задача минимизации квадратичной
целевой функции неотрицательных
переменных при линейных ограничениях.
В
дальнейшем нам понадобятся аппроксимации
целевой функции
в окрестности точки
с помощью усеченного ряда Тейлора
Линейная (или 1-го порядка):
(2.2.6)
Квадратичная (или 2-го порядка):
Приведем теперь (без доказательств) необходимые и достаточные условия оптимальности решения для общей задачи нелинейного программирования.
А. Задачи без ограничений
Необходимые
условия локального минимума в точке
:
Достаточные условия: