Методические указания к выполнению задач

В статистике применяют несколько видов средних величин: арифметическую, гармоническую, геометрическую и др. В зависимости от частоты повторения вариантов средние вычисляются как простые (не взвешенные) и взвешенные. Средняя применена правильно, если в результате получают величины, имеющие реальный экономический смысл. Средняя должна рассчитываться по качественно однородной совокупности, иначе она будет фиктивной.

Формулы для расчета:

а) средняя арифметическая простая

,

где - варианта;

- число единиц совокупности.

б) средняя арифметическая взвешенная:

,

где - частота.

Применяется тогда, когда объем варьирующего признака для всей совокупности определяется как сумма значений признаков отдельных величин.

в) средняя гармоническая простая ;

г) средняя гармоническая взвешенная ,

где - произведение варианты на частоту.

Используется тогда, когда в качестве весов применяются не единицы совокупности, а произведения этих единиц на значения признака; численность совокупности не известна;

д) средняя геометрическая простая

,

где x₁, x₂,..., x_n - значения цепных коэффициентов роста;

П - знак перемножения

е) средняя геометрическая взвешенная

.

Применяется, если задана последовательность цепных относительных величин динамики, указывающих, например, на рост объема производства или снижение уровня преступности по сравнению с уровнем предыдущего года.

Для характеристики вариационного ряда рассчитываются показатели вариации:

1. Размах вариации (R):

;

2. Среднее линейное отклонение:

;

3. Дисперсия:

;

4. Среднее квадратическое отклонение:

.

5. Коэффициент вариации:

- характеризует колеблемость признака по отношению к среднему уровню ряда.

Показатели моды и медианы определите по дискретному ряду.

Мода () - наиболее часто встречающееся значение признака в совокупности.

Медиана () - середина ранжированного ряда, т.е. величина признака, делящая ряд на две равные части. Для дискретного с нечетным числом уровней медианой будет варианта, находящаяся в середине ряда:

,

где – номер медианы.

Для дискретного ряда с четным числом медианой будет средняя арифметическая из двух вариант, расположенных в середине ряда:

.

Алгоритм определения моды и медианы для интервального ряда.

Для интервального ряда с равными интервалами мода определяется по формуле:

,

где - нижнее значение модального интервала (имеющего наибольшую частоту);

- ширина (шаг) интервала;

- частота модального интервала;

и - соответственно: частота интервала, предшествующего (последующего) модальному.

Для интервального вариационного ряда медиана определяется по формуле:

,

где - нижняя граница медианного интервала;

- его величина; - его частота;

-сумма накопленных частот в интервалах, предшествующих медианному;

- сумма частот ряда.

Для характеристики ряда распределения рассчитывают:

-коэффициент асимметрии

;

-коэффициент эксцесса

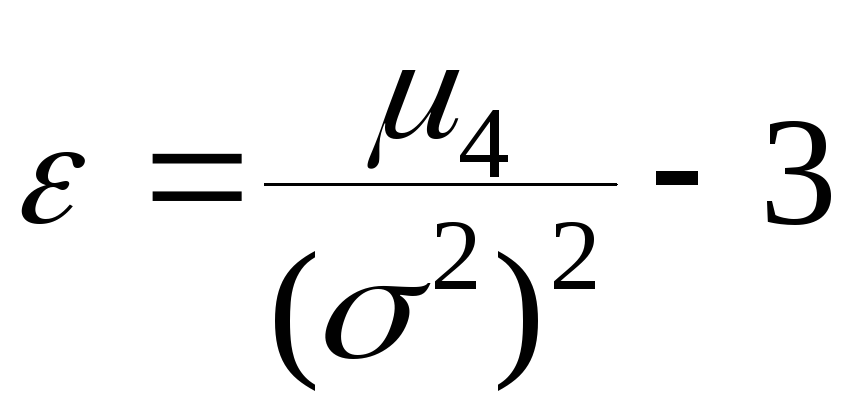, где

Тема 9. Ряды динамики

Цель: уяснение анализа рядов динамики или временных рядов, представляющих собой ряды числовых значений конкретных статистических величин за какой-то определенный отрезок времени.