методичка по моделированию

Федеральное агентство морского и речного транспорта Федеральное бюджетное образовательное учреждение высшего профессионального образования

šВолжская государственная академия водного транспортаœ

Кафедра математики

МАТЕМАТИЧЕСКИЕ МОДЕЛИ СЛОЖНЫХ СИСТЕМ

Методические указания к выполнению лабораторной работы

для студентов радиотехнической специальности 162107

Составители: В. Н. Белых, М. С. Киняпина

Нижний Новгород Издательство ФБОУ ВПО šВГАВТœ

2012

УДК 514.12 М34

Р е ц е н з е н т 4 доцент Б. С. Украинский

Математические модели сложных систем : метод. указания к выпол. лабор. работы для студ. радиотех. специальности 162107 / сост. В. Н. Белых, М. С. Киняпина 4 Н. Новгород : Издво ФБОУ ВПО šВГАВТœ, 2012. – 20 с.

Излагаются некоторые факты курса высшей математики и математического моделирования, необходимые для выполнения лабораторной работы šИсследование влияния параметров на динамическую систему, описываемую линейным дифференциальным уравнением первого порядкаœ по спецкурсу šМатематическое моделирование систем и процессовœ. Приведен пример выполнения и оформления лабораторной работы.

Для студентов специальности 162107 •Техническая эксплуатация транспортного радиооборудования˜.

Работа рекомендована к изданию кафедрой математики (протокол № 10 от 12.05.2012).

°c ФБОУ ВПО šВГАВТœ, 2012

КРАТКАЯ ТЕОРИЯ

Общая схема математического моделирования

Математическое моделирование включает решение двух задач: составление математической модели и е¨ исследование. Основные этапы математического моделирования:

1.Постановка задачи и определение объекта исследования.

2.Идеализация и упрощение объекта.

3.Составление первоначальной математической модели, выделение основных параметров.

4.Выбор и реализация методов исследования математической модели.

5.Сопоставление результатов исследования с тем, что известно об объекте.

6.Внесение корректив в математическую модель.

7.Выводы и рекомендации.

Из каждого этапа возможны возвраты к предыдущим. Необходимо учесть, что чем проще модель, тем меньше возможностей ошибиться. Модель должна быть простой, но не проще, чем это возможно. Модель должна быть грубой, малые возможные и допустимые поправки не должны кардинально менять е¨ поведение. При анализе результатов важно понимание, почему и как вс¨е происходит и как поведение системы зависит от параметров.

Рассмотрим математические модели некоторых объектов, процессов или явлений, называемых динамическими системами. Различают системы с дискретным временем и системы с непрерывным временем.

Мы ограничимся классом динамических систем, который описывается либо обыкновенными дифференциальными уравнениями, либо разностными уравнениями. Основное содержание теории динамических систем 4 это исследование кривых, определяемых дифференциальными уравнениями, 4 фазовых траекторий, притягивающих множеств (аттракторов), их областей

3

притяжения и бифуркаций. Сюда, в частности, входит разбиение фазового пространства на траектории и изменение этого разбиения при изменении параметров. Положениям равновесия динамической системы соответствуют особые точки дифференциального уравнения, а замкнутым фазовым кривым 4 его периодические решения.

Важнейшие понятие теории динамических систем 4 это устойчивость (способность системы сколь угодно долго оставаться около положения равновесия или на заданном многообразии) и грубость (сохранение свойств при малых изменениях структуры динамической системы).

Некоторые сведения о линейных дифференциальных уравнениях первого порядка

Определение. Линейное дифференциальное уравнение (ДУ)

называется неоднородным или неавтономным уравнением. Ему соответствует однородное или автономное ДУ

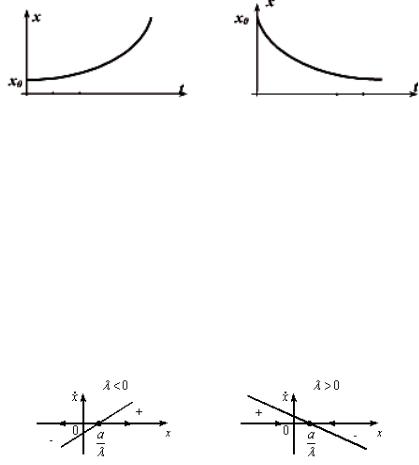
Анализ всего семейства решений: пусть x(0) = x0 4 начальное условие, тогда c = x0, x(t) = x0 · e−λt. Нулевое начальное условие x0 = 0 влечет x(t) ≡ 0. Это состояние равновесия системы 4 нулевое решение (2).

При ненулевых начальных условиях x0 6= 0 выражение x(t) = c · e−λt 4 экспоненциальный процесс (x(t) меняется экспоненциально с изменением времени), затухающий при λ > 0 (убывающий до нуля) и возрастающий при λ < 0.

4

Прямая x называется фазовой прямой, которая в этом простейшем случае играет роль фазового пространства:

Движение вдоль фазовой прямой определяет плоскость (x; x˙ ), если x˙ > 0, то x возрастает, а при x˙ < 0 величина x убывает.

При x˙ = 0 уравнение (2) имеет состояние равновесия в точке x = 0.

При λ < 0 состояние равновесия x = 0 4 неустойчиво. При λ > 0 состояние равновесия x 4 устойчиво.

Стрелка указывает движение изображающей точки во времени.

5

Случай f (t) = a = const.

Очевидно, x = λa 4 постоянное решение (4). Это состояние равновесия уравнения (4). Замена переменной в (4) на x = λa + u

приводит (4) к виду

но (5) совпадает с уравнением (2), тогда общее решение уравнения (4) записывается в виде

x = λa + ce−λt.

Общий случай f (x) в (1).

ДУ (1) решаем методом вариации произвольной постоянной: решение ищем в виде

6

Случай f (t) = a sin ωt. Рассмотрим уравнение

c(t) = e a sin ωt dt = a λ2 + ω2 (λ sin ωt − ω cos ω)t + c0 =

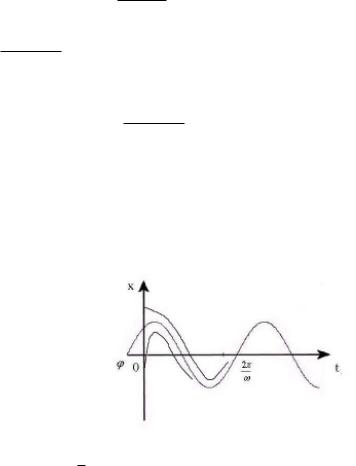
есть вынужденное, стационарное периодическое решение уравнения (1). При λ > 0, t → ∞, e−λt → 0 и стационарное решение устанавливается всегда,

т. е. lim x(t) = x (t) и

t→∞

x (t) 4 установившееся асимптотически устойчивое периодическое решение уравнения (1). Для уравнения (1) изображены периодическое движение и стремящиеся к нему траектории 4 на

плоскости (x, t). T = λ1 4 время переходного процесса.

7

Рассмотрим два примера конкретных динамических систем, приводящихся к рассмотренным уравнениям: электрический замкнутый контур с конденсатором емкости C и сопротивлением R и торможение парашюта.

На рисунке представлена схема конденсатора емкости C, разряжающегося на сопротивление R. В соответствии с законами Кирхгофа дифференциальное уравнение разряда конденсатора пишется

в виде:

Rq˙ = −Cq

или

dqdt = −τ1 q,

где τ 4 пропорционально емкости C

и сопротивлению R. Следовательно, q(t) описывается экспоненциальным убывающим процессом. При начальном заряде q = q0

t

q(t) = q0e τ .

Следующий пример 4 торможение парашюта. Пусть по достижении скорости падения v0 парашют раскрылся и тормозит падение пропорционально его скорости. Согласно закону Ньютона

mv˙ = −mg − hv.

Решение этого уравнения следующее:

Из него следует, что начальная скорость v0 (v0 > 0) экспоненциально замедляется до постоянной скорости спуска, равной mg/h. График этого процесса изображен на рисунке ниже.

8

Пример выполнения лабораторной работы )Исследование влияния параметров на динамическую систему, описываемую линейным дифференциальным уравнением первого порядка+

Задание: исследовать влияние параметров дифференциальных уравнений первого порядка с постоянными коэффициентами

Получить временные реализации и фазовые портреты, соответствующие различному поведению систем.

При данных параметрах получаем восемь систем:

Отч¨ет по лабораторной работе должен включать теоретические расч¨еты, результаты компьютерного моделирования и вывод (анализ полученных результатов).

9

Теоретический расчет проведем для системы (II). Рассмотрим однородное (автономное) уравнение. Найдем его решение: x˙ + 15x = 0 4 это ДУ с разделяющимися переменными.

Используя свойства логарифмов, найд¨ем x в явном виде:

4 общее решение автономного (однородного) уравнения. Применим метод вариации произвольной постоянной: