1.5.1.1. Использование матрицы податливости системы

В наиболее компактной матричной форме система диффе-ренциальных уравнений ( 1.14 ) представляется так:

, ( 1.16 )

где  – матрица внешней упругой податливости рассчитывае-

мой системы по направлениям возможных перемеще-

ний масс ( степеней свободы ); её компонентами явля-

ются величины _ik () – перемещения в заданной

системе по направлениям инерционных силовых факто-

ров J_i (t) ()) от единичных силовых воздействий

Свойства компонентов матрицы податливости:

1. Собственные перемещения _ii – существенно положительные.

2. Побочные перемещения облада-ют свойством взаимности ( по теореме Максвелла ): _ik =_ki при .

3. Матрица податливости – положи-тельно определённая.

J_k = 1, ( см. рис. 1.16 ):

. . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . .

;

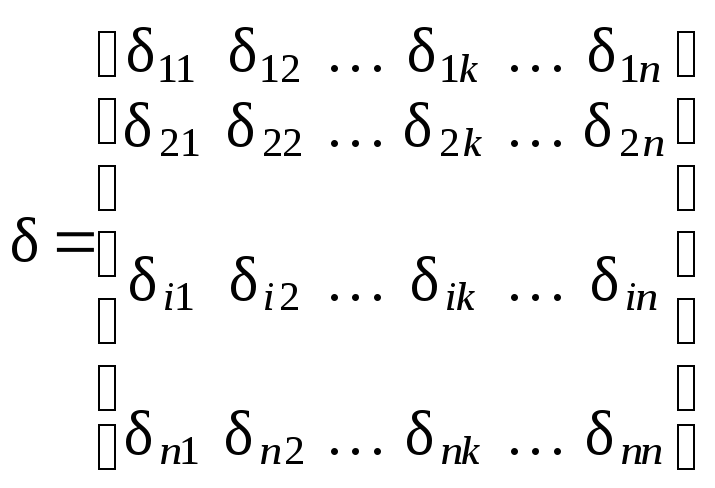– векторы функций ускорений, скоростей

и перемещений масс:

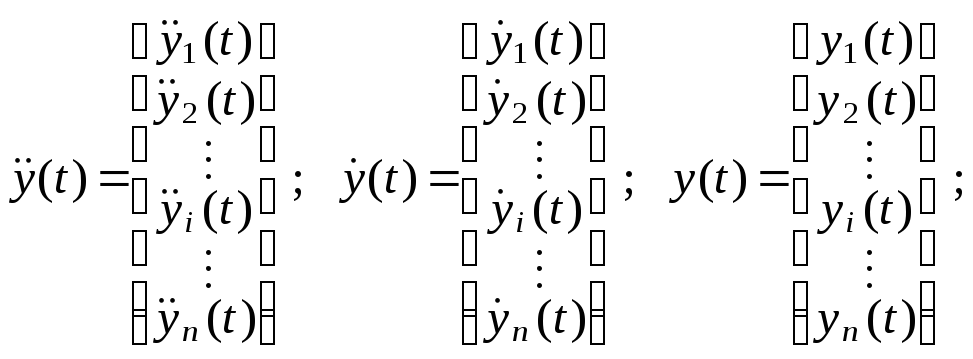
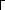
– матрица^*) обоб-

щённых ( приведённых ) масс, совершающих перемеще-

ния y_i (t) ();

– матрица

коэффициентов неупругого сопротивления движению

( применяется также термин «матрица демпфирования» );

_P – матрица перемещений от наибольших ( амплитудных )

значений заданных динамических воздействий:

. . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . .

(t) – вектор временных функций заданных воздействий:

^*) В дальнейшем будут рассмотрены случаи, когда матрица масс – недиагональная ( см. п. 1.6 ).

Уравнения ( 1.16 ) можно записывать также с разделением слагаемых, содержащих ускорения и скорости масс:

. ( 1.16*)

Матричный вариант уравнений ( 1.15 ) выглядит так:

, ( 1.15*)

где – векторы функций инерционных силовых

факторов, их первых и вторых производных:

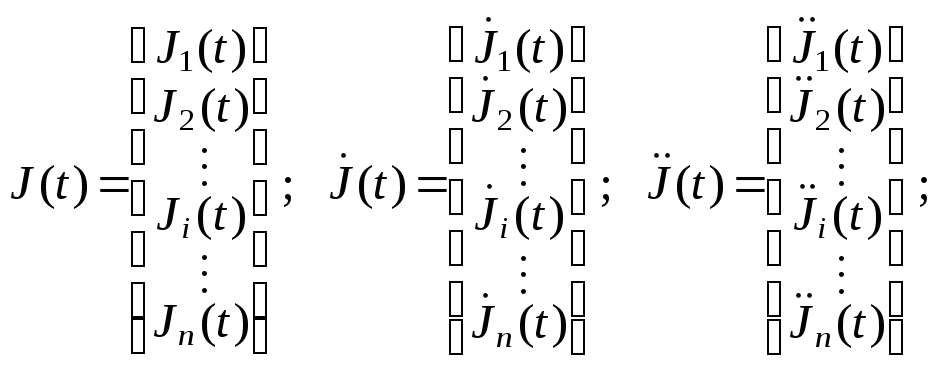
– вектор вторых производных временных функций задан-

ных воздействий:

В литературе встречаются различные обозначения мат-риц, входящих в уравнения движения: вместо  используются А, В или D; в [ 1 ] система ( 1.16*) имеет вид , существует вариант и др.

1.5.1.2. Уравнения движения с матрицей жёсткости системы

Свойства деформируемой системы, согласно принципу двойственности в механике, могут характеризоваться, наряду с матрицей упругой податливости, которая количественно оцени-вает способность системы деформироваться от механических воздействий, также матрицей жёсткости, характеризующей способность системы противостоять её деформированию. Как податливость, так и жёсткость системы оцениваются по опреде-лённым направлениям, назначаемым в зависимости от решаемой задачи. В динамике это направления компонентов перемещений масс или, что то же самое, соответствующих инерционных сило-вых факторов.

Матрица жёсткости ( обычно обозначается r ) – квадратная размерами n x n, каждый столбец которой состоит из значений силовых факторов, одновременно действующих по направлени-ям всех перемещений масс и вызывающих равное единице пере-мещение с номером, равным номеру столбца, при равенстве нулю всех остальных перемещений. Смысл компонентов k-го столбца

1

2

i

k

n

r_nk

r_ik

r_1k

r_2k

1

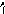
матрицы жёсткости по-

показан на примере про-

стой балки ( рис. 1.18 ),

r_kk

где в кружках даны но-

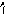
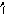
мера степеней свободы.

Рис. 1.18

Все силы формально

направлены в одну сто-

рону, но фактически некоторые из них могут быть противопо-ложными, т. е. отрицательными.

Обозначения r_1k , r_2k , …, r_ik , …, r_kk , …, r_nk приняты потому, что указанные силовые факторы могут рассматриваться как ре-акции воображаемых связей, поставленных по направлениям сте-пеней свободы, от единичного смещения k-й связи. На рис. 1.19 эти же величины представлены для ранее рассматривавшейся общей расчётной модели,

п

r_kk

r_ik

r_1k

r_{k+1, k}

y_k = 1

ричём с изображением

у

r_nk

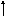
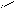
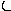
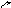
словно введённых связей

п

r_{i+1, k}

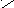
о направлениям возмож-

н

r_2k

ых перемещений масс.

Матрица жёсткости

системы ( матрица внеш-

ней жёсткости по направ-

лениям степеней свободы

масс ) имеет следующую

структуру: Рис. 1.19

. . . . . . . . . . . . . . .

. . . . . . . . . . . . . . .

Свойства компонентов матрицы жёсткости:

1. Собственные единичные реакции r_ii – существенно положительные.

2. Побочные реакции обладают свой-ством взаимности ( по теореме Рэлея ):

r_ik =r_ki при .

3. Матрица жёсткости – положитель-но определённая.

, ( 1.17 )

где r_ik () – реакция i-й

условной связи от единичного смещения k-й связи.

Компоненты матрицы жёсткости r можно находить расчё-том рассматриваемой системы на n вариантов кинематических воздействий ( последовательных смещений n связей в точках рас-положения сосредоточенных масс) известными методами теории сооружений. Но матрица жёсткости может быть также получена как обратная по отношению к матрице податливости:

r =  ^–1 – ( 1.18 )

это свойство матриц r и  доказывается в основном курсе строи-тельной механики; для систем с одной степенью свободы имеет место известная и очевидная зависимость r₁₁ = 1/₁₁ , где r₁₁ и ₁₁ – коэффициенты жёсткости и податливости соответственно.

Уравнения движения, в которых свойства деформируемой системы описываются матрицей жёсткости, получаются из сле-дующих соображений: если к безмассовой системе с дополни-тельными связями по направлениям степеней свободы масс, от-делённых от системы, приложить заданные воздействия, инер-ционные и диссипативные силовые факторы ( рис. 1.20 ), а также задать указанным связям смещения, равные динамическим пере-мещениям y₁(t), y₂ (t), …, y_i (t), …, y_k (t), …, y_n (t), то деформации, реакции опор и внутренние усилия будут такими же, как в рас-считываемой системе без связей, следовательно, полные реакции всех введённых связей станут равными нулю:

J_i (t) + F_Di (t)

R_i (t) = 0 (). ( 1.19 )

J_k+1(t) + F_{D, k+1}(t)

J_k (t) + F_Dk (t)

F(t)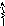

J₁(t) + F_D1(t)

J_n–1 (t) + F_{D, n–1} (t)

k

i

k +1

n

J₂(t) + F_D2(t)

2

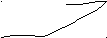
J_n (t) + F_Dn (t)

1

(t)

y

q(t)

x

z

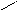
Рис. 1.20

Руководствуясь принципом суперпозиции и учитывая, что воздействия J_i (t) и F_Di (t) воспринимаются непосредственно i–й связью, полную реакцию этой связи R_i (t) представляем в виде

R_i (t) = – J_i (t) – F_Di (t) + R_iy(t) +R_iP (t) , ( 1.20 )

где R_iy (t) – составляющая реакции i-й связи от одновременных

смещений y₁(t), …, y_i (t), …, y_k (t), …, y_n (t) всех связей;

R_iP (t) – вклад в реакцию R_i (t) всех заданных воздействий.

Используя для описания доли , вносимой в R_iy(t)

с

R_iy (t) =. ( 1.21 )

мещением y_k (t) k-й связи, единичной реакции r_ik i-й связи от единичного смещения y_k = 1, получаем = r_ik y_k (t), тогда

воздействий:

Аналогично расписываем R_iP (t) по компонентам заданных

R_iP(t) =, ( 1.22 )

где – реакция i-й связи от наибольшего ( амплитудного ) зна-

чения Р_р ( см. рис. 1.15 ) р-го заданного воздействия

( величины определяются расчётом системы с за-

креплёнными точками расположения масс на n_p вари-

антов воздействий Р_р ).

З а м е ч а н и е: если заданные воздействия приведены к эквивалент-

ным силам F_eqvl (t), приложенным в точках расположения масс, что является

стандартной процедурой в расчётах методом конечных элементов, реакции оказываются равными амплитудам соответствующих эквивалентных сил и

направленными противоположно им.

Подстановка ( 1.21 ) и ( 1.22 ) в ( 1.20 ) и учёт ( 1.19 ) даёт

– J_i (t) – F_Di (t) + += 0 , . ( 1.23 )

Если выбрать в качестве основных неизвестных функции перемещений y(t), то после использования ( 1.2 ) и ( 1.3 ) для вы-ражения J(t) и F_D (t) через производные от y(t), получаем систему дифференциальных уравнений движения масс

+ k_f,i+= –, ( 1.24 )

или в развёрнутом виде:

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

( 1.25 )

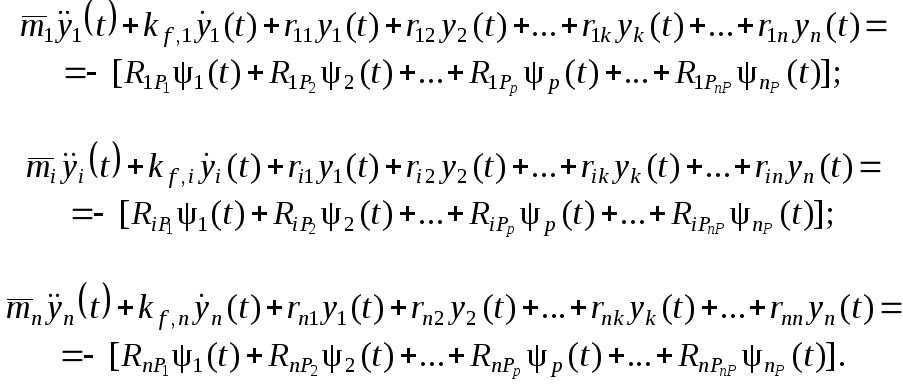
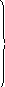
В компактной матричной записи уравнения ( 1.25 ) пред-ставляются так:

, ( 1.26 )

где

. . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . .

– матрица реакций связей по направлениям компонентов пе-ремещений масс от наибольших (амплитудных) значений задан-ных динамических воздействий;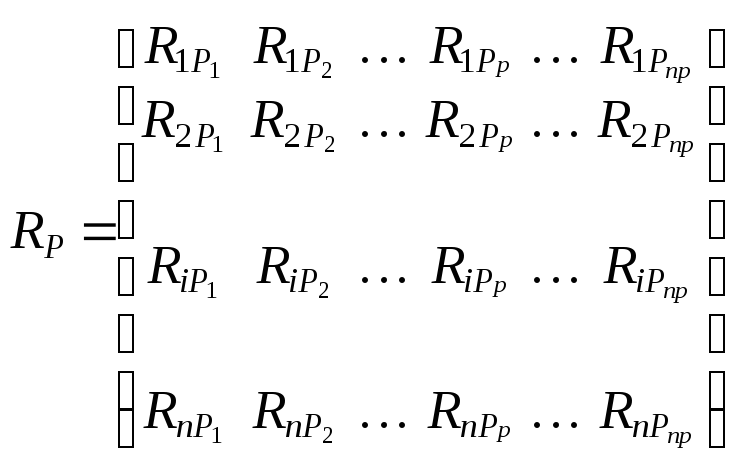

остальные матрицы – как в ( 1.16 ).

Из ( 1.24 ) двойным дифференцированием ( подобно тому, как это было сделано при переходе от ( 1.14 ) к ( 1.15 )) получа-ются уравнения движения с функциями инерционных сил J(t) в качестве основных неизвестных:

+ k_{f, i} +=, ; ( 1.27 )

в матричной форме:

+ k_f +=. ( 1.28 )

Иные встречающиеся в литературе представления матрич-ных уравнений ( 1.26 ) с другими обозначениями величин:

[ 1 ], и др.