1.5. Уравнения динамики деформируемых систем с конечным числом степеней свободы масс

F(t)

Рассматривается линейно деформируемая система произ-вольного типа и структуры^*) ( рис. 1.13, а ) с невесомыми ( безмас-совыми) элементами, несущая сосредоточенные массы – точеч-ные и неточечные ( последние прикрепляются к элементам и уз-

лам на уровне центров

тяжести )^**) при пере-

а) менных во времени

( динамических ) меха-

нических воздействи-

q(t)

ях – силовых и кине-

матических. Её дефор-

(t)

y_k (t)

y_k+1(t)

мированное состояние

в произвольный мо-

F(t)

y_n–1 (t)

мент движения пока-

y₁(t)

y_i (t)

зано на рис. 1.13, б.

y_i+1(t)

Обозначенные на

y₂(t)

схеме компоненты не-

б

y_n (t)

) зависимых перемеще-

q(t)

y

ний – линейных и (для

неточечных масс ) уг-

z

ловых принимаются в

(t)

x

качестве степеней сво-

Рис. 1.13

боды масс. Они отсчи-

^*) Конкретные особенности системы не имеют принципиального значения при форми-ровании математической модели задачи ( выводе основных уравнений и формул ) – можно было бы рассмотреть некое обобщённое деформируемое твёрдое тело ( конти-нуум ), обладающее свойством линейной упругости.

^**) Случай эксцентричного прикрепления будет рассмотрен дополнительно в п. 1.6.

тываются от положения статического равновесия системы, изо-бражённого штриховыми линиями и рассматриваемого как ус-ловно недеформированное. Их направления, а также правила знаков, могут назначаться произвольно, но целесообразно свя-зывать их с общими ( глобальными ) осями координат x, y, z, если нет других рациональных аргументов. Нумеровать степени сво-боды ( перемещения ) от 1 до n можно тоже в произвольном по-рядке, но есть смысл придерживаться какой-либо системы.

Следуя предпосылкам и гипотезам линейной теории ( см. п. 1.3 ) и применяя кинетостатический метод, прикла-дываем к невесомой системе в точках прикрепления отделённых

от неё масс диссипативные силы и моменты F_Di (t) ( i = ) и д’аламберовы инерционные силовые факторы J_i (t) ( i = )^*) ,

р

y_k (t)

ассматриривая их совместно с заданными динамическими воз-действиями F(t), q(t), (t) ( рис. 1.14 ).

y_k+1(t)

J_k (t)

J_i (t)

J_k+1(t)

J_n–1 (t)

F(t)

J₁(t)

J_i+1(t)

F_{D, i+1}(t)

y_i (t)

y_n–1 (t)

F_{D, k+1}(t)

F_D2(t)

J_n (t)

F_Dn (t)

F_Dk (t)

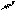
y₁(t)

y_i+1(t)

J₂(t)

F_Di (t)

F_D1(t)

F_{D, n–1} (t)

y₂(t)

y_n (t)

q(t)

(t)

y

z

x

Рис. 1.14

Номера и направления инерционных и диссипативных си-ловых факторов J_i (t) и F_Di (t) ( i = 1, 2, ..., n ) назначаются такими же, как у соответствующих перемещений ( степеней свободы ).

^*) Точнее – равные им реакции связей, прикреплявших к системе

удалённые массы ( см. разъяснения к рис. 1.5 ).