
- •Основные положения теории динамических расчётов деформируемых систем с конечным числом степеней свободы масс
- •1.1. Термины, понятия и определения
- •1.2. Основные символы и обозначения
- •1.3. Предпосылки и гипотезы динамического расчёта. Принципиальная расчётная модель деформируемой системы с сосредоточенными массами
- •1.4. Степени свободы масс
- •1.5. Уравнения динамики деформируемых систем с конечным числом степеней свободы масс
- •1.5.1. Уравнения для общего случая движения
- •1.5.1.1. Использование матрицы податливости системы
- •1.5.1.2. Уравнения движения с матрицей жёсткости системы
- •1.5.2. Систематизация и анализ вариантов уравнений динамики
- •1.5.3. О численном решении уравнений динамики систем с конечным числом степеней свободы масс
- •1.5.4. Свободное движение и собственные колебания
- •1.5.4.1. Уравнения свободного движения, их решение;
- •1.5.4.2. Характеристическое ( частотное ) уравнение;
- •Дополнительные сведения о собственных векторах j и y
- •1.5.4.4. Расчёт на собственные колебания
- •1.5.5. Вынужденное движение; установившиеся колебания от вибрационных воздействий
- •1.6. Обобщённые перемещения, группировка неизвестных и учет симметрии в динамических расчётах
- •1.7. О приближённом определении частот
- •2. Некоторые инженерные приложения динамики систем с конечным числом степеней свободы масс
- •2.1. Кинематическое возбуждение движения деформируемой системы. Понятие о расчёте на сейсмические воздействия
- •2.2. Понятие об аэроупругости и расчётах сооружений на ветровые нагрузки
- •2.3. Защита сооружений и конструкций от динамических воздействий
- •3. Примеры динамических расчётов статически неопределимых стержневых систем с сосредоточенными массами
- •Задача 3.1. Расчёт плоской стержневой системы на собственные и вынужденные колебания
- •3.1.1. Динамический расчёт рамы
2.3. Защита сооружений и конструкций от динамических воздействий
В технике переменность во времени параметров состояния инженерной системы или устройства в некоторых случаях мо-жет быть полезным фактором. Например, на явлении электро-магнитного резонанса основаны передача и приём радио- и теле-сигналов; виброударные машины и оборудование применяются в различных технологических процессах, в том числе в строи-тельстве, и т. д. Но для зданий, сооружений и строительных кон-струкций динамические воздействия значимой интенсивности и продолжительности практически всегда рассматриваются как угрозы, которым нужно противостоять с целью недопущения опасных последствий для прочности, устойчивости, жёсткости и других эксплуатационных качеств строительной системы, вклю-чая и условия безопасной жизнедеятельности людей. Последнее очень важно, так как даже при технически допустимых и не уг-рожающих механической работоспособности сооружения виб-рациях и сотрясениях их физиологическое воздействие на лю-дей может быть вредоносным. В ряде случаев определяющими бывают требования обеспечения необходимых условий для нор-мальной работы различных ( в частности, прецизионных ) при-боров, механизмов, оборудования, расположенных в здании или сооружении. Соответствующие количественные ограничения ди-намических параметров ( амплитуд перемещений, скоростей, ускорений и др. ) содержатся в нормативных документах.
К настоящему времени в достаточной мере сформирова-ны и продолжают развиваться и совершенствоваться теорети-ческие основы защиты от динамических воздействий как осо-бого раздела динамики сооружений. Конструктивные решения ( включая специальные устройства ), обеспечивающие уменьше-ние динамических перемещений, усилий и напряжений, много-численны и разнообразны – эти технические вопросы, не отно-сящиеся к предмету строительной механики, здесь не обсужда-ются в деталях.
Важными инженерными проблемами динамики строитель-ных систем являются
противодействие сейсмическим воздействиям (сейсмозащита);
защита высотных и большепролётных сооружений от аэроди-
намических нагрузок;
гашение колебаний, вызванных вибрационными воздействиями
( виброзащита );
защита от специальных видов динамических воздействий ( уда-
ров, взрывов и др. ).
Влиять на характеристики заданных воздействий с целью их изменения в желательном направлении удаётся лишь в редких случаях, а для воздействий природного происхождения это про-сто невозможно. Поэтому главным принципом динамической защиты является целенаправленное изменение жесткостных, демпфирующих и инерционных свойств самой деформируемой системы или особых устройств ( гасителей колебаний ). В такой интерпретации задачи защиты зданий, соружений и конструк-ций относятся к задачам регулирования их динамического на-пряжённо-деформированного состояния [ 7 ].
Некоторые способы, средства и устройства защиты доста-точно универсальны и пригодны для решения разных вышена-званных проблем. Например, рассматриваемые далее гасители колебаний применимы и в сейсмозащите, и в борьбе с вибраци-ей, и для уменьшения аэроколебаний – конечно, с различными конструктивными особенностями и динамическими характерис-тиками. Другие имеют специальное назначение и создаются для противодействия динамическим воздействиям определённого вида.
В любом случае параметры средств ( устройств ) динами-ческой защиты должны назначаться на основе тщательного рас-чёта. Чрезвычйно опасно принимать инженерные решения исхо-дя из общих умозрительных соображений типа «нужно умень-шить вибрацию – поставим мягкую прокладку». Результат может быть прямо противоположным желаемому – примеры будут даны ниже.
Сейсмозащита
зданий и сооружений принципиально осуществляется по следу-ющим основным направлениям:
а) обеспечение прочности надземной части сооружения ( путём создания поясов жёсткости, диафрагм и т. п. ) и гашение её колебаний специальными устройствами;
б) уменьшение передаваемых на сооружение воздействий от сейсмических смещений основания ( некоторые возможные решения: реализация «плавающего» опирания верхней части на фундамент, при котором само сооружение за счёт своей инерт-ности получает значительно меньшие перемещения, чем основа-ние; введение в систему конструктивных элементов между зда-нием и фундаментом, либо выключающихся ( в том числе квази-хрупко разрушающихся ) при сейсмическом ударе, либо, напро-тив, поглощающих энергию сейсмических волн за счёт пласти-ческого деформирования или вязкого демпфирования ).
Наибольший эффект защиты достигается совместным применением обоих подходов.
Гашение аэроколебаний
большепролётных и высотных объектов может быть
а) конструкционным ( посредством расчётного назначения необходимых параметров изгибной, крутильной жёсткостей, демпфирующих свойств конструкций и механических гасителей колебаний ) – так называемый американский путь [ 14 ];
б) аэродинамическим ( за счёт улучшения аэродинамичес-ких качеств системы – создания плавной ( обтекаемой ) формы сечений и конфигурации самой конструкции или применения навесных обтекателей, а также аэродинамических гасителей и расположенных определённым образом прорезей, щелей и перфо-рации ) – европейский подход.
Виброзащита
инженерных систем, в том числе зданий, сооружений и строи-тельных конструкций является важной динамической задачей, так как воздействие колебаний может быть опасным для проч-ности материала при переменных во времени напряжениях ( см. с. 76 ), особенно в состояниях, близких к резонансу. Поэтому для уменьшения динамических эффектов желательно не допус-кать сближения частот вынужденных и собственных колебаний F и . Как правило, изменять заданную частоту вибрационно-го воздействия F невозможно, тогда для выполнения условия ненаступления резонанса ( 1.85 ) или для получения допустимо-го значения динамического коэффициента требуется увеличение собственной частоты . Согласно формуле ( 1.32 ), качественно раскрывающей влияние на частоту различных характеристик системы, изменение в большую сторону возможно либо за счёт повышения обобщённой жёсткости с, либо путём умень-шения приведённой массы m или/и коэффициента вязкого со-
противления kf . Последнее ( для kf ) не только трудноосущест-
вимо, но и нецелесообразно, так как благоприятный рост часто-ты сопровождается значительно большим нежелательным уве-личением динамических коэффициентов перемещений и усилий в системе. Сколько-нибудь значительно уменьшить массу m хо-рошо запроектированной конструкции затруднительно, поэтому реальным остаётся регулирование частоты за счёт изменения ( увеличения ) жёсткости с, причём эффективными способами – применением тонкостенных профилей сечений, введением до-полнительных связей ( включая замену шарнирных соединений элементов жёсткими и т. п. ). Для систем с n > 1 отыскание жест-костных характеристик, обеспечивающих допустимые значения частоты или динамических усилий / напряжений, выполняется последовательными итерационными перерасчётами.
Различают два основных принципа противодействия виб-рации ( виброзащиты ) – конструкционный и динамический. Первый предусматривает целенаправленное назначение или из-менение жесткостных, демпфирующих и инерционных свойств самой системы ( сооружения, конструкции ) – по существу он из-ложен выше. Второй предполагает использование специальных устройств и приспособлений,
в
Наименования
принципов «конструкци-онный» и
«динамический» являются ус-ловными,
так как оба направлены на улучшение
динамических свойств систе-мы посредством
использования в качест-ве регуляторов
в одном случае собствен-ных параметров
конструкции, а в другом случае –
дополнительных устройств.
шения амплитуд её колебаний;
причём, в зависимости от реа-
лизуемых эффектов, различают
виброизоляцию и виброгаше-
ние.
Виброизоляция
F
(t)
ИК
m1
д
ЗО

ц
m2















н
F
(t)
ЗО
к
ИК
m1







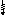

m2
ш


 ения
колебаний
объекта,
располо-
ения
колебаний
объекта,
располо-
женного на вибрирующей конструк-
ции ( рис. 2.9, б ). Рис. 2.9
На схемах рис. 2.9 массу m2 следует рассматривать как обобщённую характеристику, моделирующую инерционные свойства деформируемой системы.
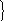
![]() (
2.4
)
(
2.4
)
где 11 = 11, 0 + 1/ ca ; ca – жёсткость амортизатора;
11, 0 – перемещение точки основной конструкции;
при этом в случае «а» 1F = 11F , 2F = 21F ;
а в случае «б» 1F = 12F , 2F = 22F .
Попытка
потребовать, чтобы в случае «а» конструкция
не испытывала вибрации (
для этого
должны быть R1
= J1
+
F
= 0 и J2
= 0 )
приводит к заключению, вытекающему из
1-го уравнения (
2.4
), о том, что
это возможно лишь при
![]() .
Следова-тельно, полное
устранение вибрации защищаемого объекта
c
помощью
амортизатора
неосуществимо.
Но можно ввести ог-раничение для
силы R1,
передаваемой
на конструкцию
через
виб-розащиту, в
виде некоторой её доли от амплитуды
нагрузки F:
R1
=
kF
F,
тогда система
уравнений (
2.4
)
даёт
формулу для
определения характеристики виброизолятора:
.
Следова-тельно, полное
устранение вибрации защищаемого объекта
c
помощью
амортизатора
неосуществимо.
Но можно ввести ог-раничение для
силы R1,
передаваемой
на конструкцию
через
виб-розащиту, в
виде некоторой её доли от амплитуды
нагрузки F:
R1
=
kF
F,
тогда система
уравнений (
2.4
)
даёт
формулу для
определения характеристики виброизолятора:
![]() (
2.5
)
(
2.5
)
Для балки, изображённой на рис. 2.10, 22 = 11, 0 , 12 =
= F
J1
J2 m



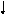
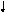
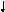
![]() ,
и из ( 2.5
) получаем
,
и из ( 2.5
) получаем
ИК
ЗО m EI
l
/
2
l
/
2
l
/
2
l
/
2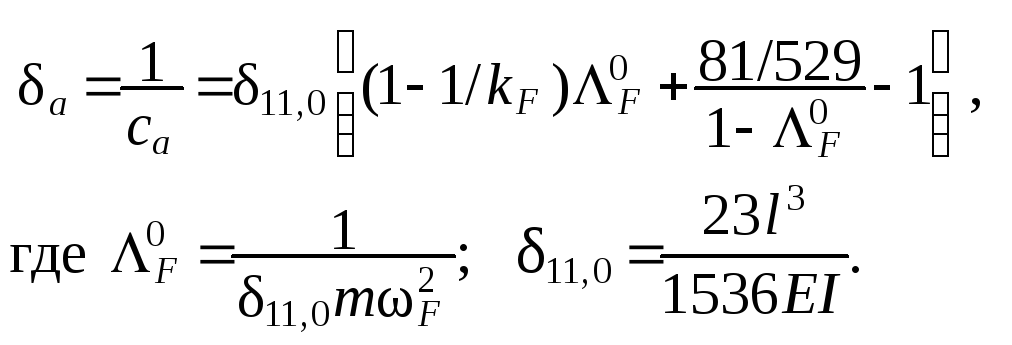


















Если задана частота F = 0,85 min , Рис. 2.10
то, вычислив для
системы без виброизоляции min=![]() ,
находим
,
находим
![]() =1,9257
и
определяем
динамический
коэффициент
=1,9257
и
определяем
динамический
коэффициент
по наибольшему
изгибающему моменту M
= 2,780. Далее
по приведённой выше формуле
вычисляем a
=
1/ca
= 11,
0
(
0,7603
–
– 1,9257
/
kF
). Для того,
чтобы податливость
/
жёсткость
аморти-затора была реальной (
положительной
), должно
быть выполне-но условие kF
![]() или kF
< 0. Назначив близкое к мини-мально
допустимому
положительное
значение kF
=
2,6, получаем
или kF
< 0. Назначив близкое к мини-мально
допустимому
положительное
значение kF
=
2,6, получаем
a
=
1/ca![]() 0,02
11,
0
. Выполнив
расчёт по уравнениям (
2.4
), нахо-
0,02
11,
0
. Выполнив
расчёт по уравнениям (
2.4
), нахо-
дим динамический коэффициент для балки с амортизатором: M, a = 2,855 > M = 2,780 – результат противоположен жела-емому: виброизолятор ухудшил работу конструкции. Попытка применить более мягкий амортизатор, например, с a = 0,2 11, 0 даёт ещё большее значение M, a = 3,772.
Объяснение
этому кроется в принципиальной особенности
работы виброизоляции: система
с правильно запроектирован-ным
амортизатором всегда работает в
зарезонансном режи-ме
( при
F
> min
), когда
движение масс происходит в
проти-вофазе нагрузке.
Для доказательства этого предположим,
что при
заданной частоте F
условие ненаступления резонанса
( 1.85
) выполняется,
но динамический коэффициент недопусти-мо
велик. Постановкой амортизатора, имеющего
некоторую конечную жёсткость
са
, увеличить
min
в правой части
(
1.85
) невозможно:
в исходной,
без амортизатора, конструкции масса m1
прикреплена жёстко,
что формально описывается как
![]() ,
следовательно, задание конечного
значения са
снижает
обоб-щённую жёсткость системы, при этом
частота min
уменьшает-ся
. Но если
при этом min
изменяется настолько, что становится
меньше F
, то
динамический коэффициент может оказаться
меньше, чем в незащищённой конструкции
( для
точек
нисходя-щей
ветви графика на рис.
1.29
). Такой
эффект соответствует отрицательным
значениям коэффициента kF
.
,
следовательно, задание конечного
значения са
снижает
обоб-щённую жёсткость системы, при этом
частота min
уменьшает-ся
. Но если
при этом min
изменяется настолько, что становится
меньше F
, то
динамический коэффициент может оказаться
меньше, чем в незащищённой конструкции
( для
точек
нисходя-щей
ветви графика на рис.
1.29
). Такой
эффект соответствует отрицательным
значениям коэффициента kF
.
Возвращаясь
к рассматриваемой
балке, назначаем
kF
=
–1,5 и находим
a![]() 2
11,
0
; соответствующий
динамический коэффи-циент M,
a
=
–
1,705 (
знак « – »
свидетельствует о направлении силы
инерции J1
, противоположном
нагрузке F
) – эффект
виб-розащиты очевиден.
Но если назначать податливость виброизо-
лятора «наугад», без расчёта, то можно
и в зарезонансной обла-сти получить
негативный результат. Например, задав
a
=
11,
0 ,
будем иметь динамический коффициент
M,
a
=
–
8,817 – в три
с лишним раза больше (!), чем в незащищённой
конструкции – такой «амортизатор»
безусловно вреден.
2
11,
0
; соответствующий
динамический коэффи-циент M,
a
=
–
1,705 (
знак « – »
свидетельствует о направлении силы
инерции J1
, противоположном
нагрузке F
) – эффект
виб-розащиты очевиден.
Но если назначать податливость виброизо-
лятора «наугад», без расчёта, то можно
и в зарезонансной обла-сти получить
негативный результат. Например, задав
a
=
11,
0 ,
будем иметь динамический коффициент
M,
a
=
–
8,817 – в три
с лишним раза больше (!), чем в незащищённой
конструкции – такой «амортизатор»
безусловно вреден.
Заметим, что, во первых, уменьшив нежелательное влияние вибрации на несущую конструкцию, нужно оценить, не окажут-ся ли недопустимо большими колебания источника ( машины, ус-тановки ), и во-вторых, следует выполнять проверку на прохож-дение зоны резонанса при включении и выключении источника вибрации ( учёт демпфирующих свойств системы обязателен ).
Для кинематической виброзащиты (см. рис. 2.9, б) из урав-нений ( 2.4 ) получается зависимость между силами инерции
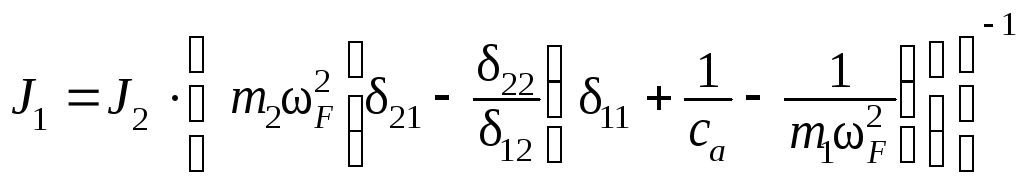 ,
( 2.6
)
,
( 2.6
)
согласно которой для уменьшения J1 и, следовательно, амплиту-ды колебаний защищаемого объекта нужно увеличивать подат-ливость a = 1/ca виброизоляции до максимально возможного предела. Этот принцип положен в основу ряда технических ре-шений сейсмозащиты, включая упоминавшееся выше «плаваю-щее» опирание надземной части сооружения на фундамент.
Гашение колебаний
как направление в теории и практике защиты инженерных сис-тем от вибрационных воздействий предусматривает использова-ние специальных устройств, называемых гасителями колебаний, присоединённых к защищаемому объекту с целью изменения ( улучшения ) его динамического состояния [ 9 ].
Существуют самые разнообразные по техническим и кон-структивным особенностям гасители колебаний ( ГК ), в том числе применяемые для защиты строительных объектов. Их можно классифицировать по следующим основным признакам:
по количеству масс – одномассовые и многомассовые;
по характеру взимодействия масс с защищаемым объектом –
безударные ( динамические ) и ударные ( с соударениями масс );
по свойствам связей в составе гасителя – ГК с упругими свя-
зями, ГК с демпфирующими связями, ГК с выключающимися
связями;
по возможности изменения параметров гасителя – регулируе-
мые и нерегулируемые;
по наличию автоподстройки к режиму колебаний – активные
( с авторегулированием ) и пассивные ( без обратной связи и
автоподстройки ).
пассивные
(
без
обратной связи
и
автоподстройки
)
п A
Защищаемый
объект
F
(t)
с

 помощью
которой
масса
гасителя
прикреп-
помощью
которой
масса
гасителя
прикреп-
л
cd
н
md
Гаситель
колебаний





сителя колебаний ( ДОГК ) с упругой связью
п
Направление
движения
точки А
ветственно масса и жёсткость упругого эле-
мента гасителя. Рис. 2.11
Разные по конструктивным решениям ДОГК применяются как средство уменьшения аэродинамических колебаний высот-
а) б) ных объектов – многоэтажных













 зданий и
башен (
рис.
2.12,
а,
б
),
зданий и
башен (
рис.
2.12,
а,
б
),
в




 )
подавления
раскачивания
про-
)
подавления
раскачивания
про-
 водов
ЛЭП (
рис.
2.12,
в
)
и
т.
д.
водов
ЛЭП (
рис.
2.12,
в
)
и
т.
д.
В
 башне
показан
струнный
га-
башне
показан
струнный
га-
с итель
с натянутым тросом
в ка-
итель
с натянутым тросом
в ка-
ч естве
упругого элемента.
На
естве
упругого элемента.
На
Рис. 2.12






тели», прикреплённая к прово-
ду, гасит его колебания за счёт вращательных движений.
Наибольший эффект гашения получается при размещении гасителя в месте действия на сооружение ( конструкцию ) сосре-
доточенной вибрационной нагрузки.
Добавление к объекту защиты ( деформируемой системе с n степеней свободы масс ) дополнительной массы гасителя, име-щей обычно одну степень свободы относительно системы, уве-личивает на 1 общее число степеней свободы масс системы с гасителем. Далее будет показано, что в случае одиночной сосре-доточенной вибрационной нагрузки оказывается возможным полностью исключить колебания защищаемого объекта при определённых, назначаемых по результатам расчёта, параметрах md и cd гасителя – такое устройство называется идеальным гаси-телем колебаний.
Описание ДОГК и его возможностей обычно даётся на модели защищаемой системы с одной степенью свободы масс. Покажем, что это можно сделать для системы с любым конеч-ным числом степеней свободы.
mn
Jk
(t)
Jn
(t)
F
(t)
т
mk


=
md
mi
m1
cd
Ji
(t)
J1
(t)










ж




 енной
силой F(t),
прикре-
енной
силой F(t),
прикре-
п
Jn+1
(t)
Гаситель
колебаний


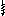
С учётом массы гаси-
т
Рис. 2.13
свободы масс составляет
n0
=
n
+
1. Для
удобства записи и анализа уравнений
пронуме-руем амплитуды инерционных сил
так, чтобы сила инерции мас-сы, на которую
действует нагрузка F(t),
оказалась предпослед-ней (
Jn
), а инерционная
сила массы гасителя – последней
( Jn+1![]() ).
Система уравнений в амплитудах инерционных
сил и нагрузки записывается как
).
Система уравнений в амплитудах инерционных
сил и нагрузки записывается как
![]() (
2.7
)
(
2.7
)
где
![]() а в двух последних уравнениях:
а в двух последних уравнениях:
![]()
![]() (
здесь
(
здесь![]() );
);
![]() .
.
Ввиду
совпадения линий действия сил Jn
и
![]() масс,
свя-занных упругим элементом гасителя,
единичные перемещения, являющиеся
коэффициентами в двух последних
уравнениях, оказываются попарно равными:
nk
= n+1,
k
(
масс,
свя-занных упругим элементом гасителя,
единичные перемещения, являющиеся
коэффициентами в двух последних
уравнениях, оказываются попарно равными:
nk
= n+1,
k
(![]() .
.
Введя требование устранения перемещения загруженной массы yn = 0, откуда Jn = 0, получаем эти два уравнения в виде
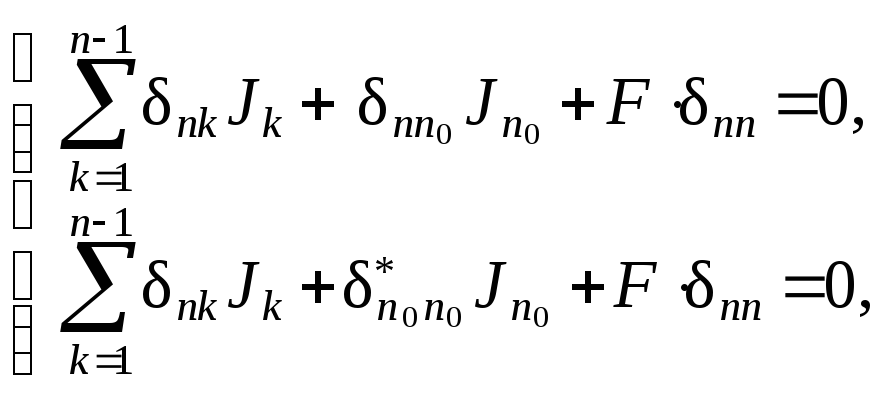 (
2.8
)
(
2.8
)
из которых вычитанием
находим
![]() ,
что даёт либо
,
что даёт либо
![]() ,
( это
не имеет смысла
–
гаситель не
работает ),
либо
,
( это
не имеет смысла
–
гаситель не
работает ),
либо
![]() ,
откуда при
,
откуда при
![]() получается
получается

![]() – (
2.9
)
– (
2.9
)
зависимость между параметрами идеального гасителя.
При этом
![]() .
(
2.10
)
.
(
2.10
)
Остальные уравнения ( с 1-го по n – 1 ) таковы:
![]() (
2.11
)
(
2.11
)
Подстановка ( 2.10 ) в ( 2.11 ) даёт:
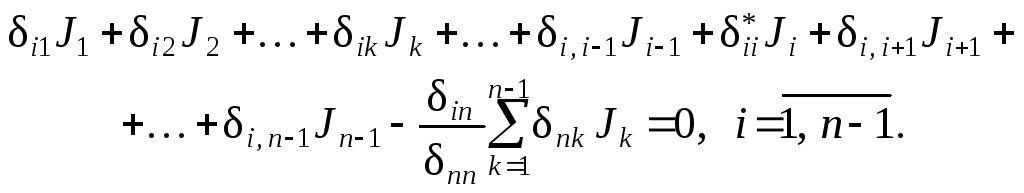 (
2.12
)
(
2.12
)
Уравнения (
2.12
) – однородные,
их тривиальное реше-ние: J1
= J2
= … = Jn
–1 =
0, следовательно, все массы системы,
кроме массы гасителя, неподвижны, а
![]() (
из (
2.10
)). Это
означает, что масса
идеального гасителя
движется в
противо-фазе нагрузке.
Иногда говорят, что имеет место
антирезонанс
– в том смысле, что обеспечивается
неподвижность всех масс за-щищаемого
объекта за счёт «перетока» энергии в
колебательное движение гасителя (
как линейного
осциллятора с собственной частотой d
= F
) с
амплитудой yd
=
F
/
cd
– эту величину следует контролировать
на непревышение допустимого предела
по тех-ническим или эксплуатационным
соображениям. При этом нуж-но иметь в
виду, что исходным для определения
параметров га-сителя является, как
правило, назначение массы md
,
после чего
жёсткость cd
находится из (
2.9
) как
(
из (
2.10
)). Это
означает, что масса
идеального гасителя
движется в
противо-фазе нагрузке.
Иногда говорят, что имеет место
антирезонанс
– в том смысле, что обеспечивается
неподвижность всех масс за-щищаемого
объекта за счёт «перетока» энергии в
колебательное движение гасителя (
как линейного
осциллятора с собственной частотой d
= F
) с
амплитудой yd
=
F
/
cd
– эту величину следует контролировать
на непревышение допустимого предела
по тех-ническим или эксплуатационным
соображениям. При этом нуж-но иметь в
виду, что исходным для определения
параметров га-сителя является, как
правило, назначение массы md
,
после чего
жёсткость cd
находится из (
2.9
) как
![]() .
Масса гасителя не должна быть слишком
большой, чтобы её вес не внёс зна-чительной
добавки к статическим усилиям в системе.
В то же время md
не
может быть очень малой, так как в этом
случае и жёсткость упругой связи
идеального гасителя получается также
малой, вследствие чего амплитуда
колебаний yd
может
оказаться недопустимо большой.
Если ограничение по yd
является
опреде-ляющим, то сначала назначается
cd
=
F
/
[ yd
] (
здесь
[ yd
] –
допу-стимая амплитуда
), а затем
вычисляется масса идеального гаси-теля
.
Масса гасителя не должна быть слишком
большой, чтобы её вес не внёс зна-чительной
добавки к статическим усилиям в системе.
В то же время md
не
может быть очень малой, так как в этом
случае и жёсткость упругой связи
идеального гасителя получается также
малой, вследствие чего амплитуда
колебаний yd
может
оказаться недопустимо большой.
Если ограничение по yd
является
опреде-ляющим, то сначала назначается
cd
=
F
/
[ yd
] (
здесь
[ yd
] –
допу-стимая амплитуда
), а затем
вычисляется масса идеального гаси-теля
![]() .
Для разных по масштабам и конструктивным
особенностям зданий и сооружений массы
динамических гаси-телей колебаний
составляют от 1
% до 5
% массы
защищаемого объекта.
.
Для разных по масштабам и конструктивным
особенностям зданий и сооружений массы
динамических гаси-телей колебаний
составляют от 1
% до 5
% массы
защищаемого объекта.
При неоптимальных ( неидеальных ) параметрах гасителя амплитуды инерционных сил находятся решением системы
уравнений, получаемой из ( 2.7 ):
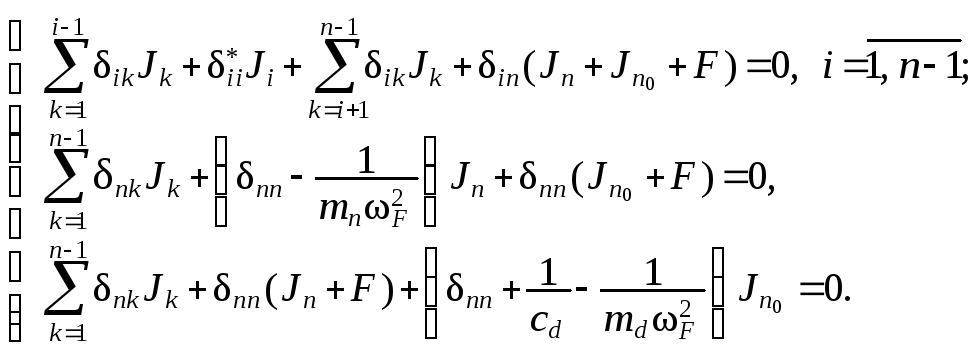 (
2.13
)
(
2.13
)
Далее обычным путём вычисляются динамические усилия и перемещения.
Частоты собственных колебаний системы с неидеальным гасителем определяются из частотного уравнения
Det ( A – B ) = 0, ( 2.14 )
г
. . . . . . . . . . . . . . .
. . . . . . . .
dik
=
ik
C0
.
При проектировании динамических гасителей нужно иметь в виду следующее:
1. Низшая частота 1 собственных колебаний системы, за-щищённой гасителем, очень близка к заданной частоте F виб-рационной нагрузки.
2. Частота 1 меньше частоты F , поэтому возможно про-явление резонансного эффекта в периоды «разгона» и выключе-ния источника вибрационного воздействия, что требует расчёта на прохождение зоны резонанса с учётом демпфирующих ( вяз-ких ) свойств системы.
3. При случайных вариациях расчётных параметров защи-щаемого объекта, гасителя и частоты нагрузки возрастает риск резонанса на низшей фактической собственной частоте защи-щённой системы при отклонениях от проектной частоты F . Возникает также риск резонанса на второй собственной частоте 2 , которая у системы с гасителем оказывается значительно бли-же к низшей 1, чем у исходной ( незащищённой ) конструкции.
4. В диапазоне частот 1 … 2 системы с гасителем, ввиду его относительной узости (2 /1 = 1,2 … 1,5), динамические ко-эффициенты могут быть значительными и даже сопоставимыми по значениям с характеристиками незащищённой конструкции в рабочем режиме, что может сделать применение гасителя неце-лесообразным ( пример приведён в гл. 3 ).
5. Повышенные требования к точности расчёта парамет-ров и к изготовлению гасителя должны предъявляться в случае динамической защиты объекта, у которого несколько собствен-ных частот близки к рабочей частоте F , во избежание попада-ния в резонанс на одной из них вследствие отклонений от про-ектных характеристик гасителя.
В заключение отметим, что с помощью ДОГК невозможно полностью уничтожить колебания при вибрационных воздейст-виях, приложенных в нескольких точках ( или распределённых ). Но при правильно рассчитанных параметрах гасителя вибрация может быть существенно ослаблена. Лучший эффект получается от применения многомассовых устройств гашения колебаний.
