2.2. Понятие об аэроупругости и расчётах сооружений на ветровые нагрузки

z

Ветровые воздействия на здания и сооружения, имеющие высоты, соизмеримые с размерами в плане, как правило, не яв-ляются определяющими в сравнении с другими нагрузками и поэтому могут учитываться на основании сравнительно простых моделей. Так, если рассматривать здание как преграду на пути набегающего воздушного потока ( рис. 2.6, а ), то за счёт его торможения на наветренных поверхностях возникает давление, называемое ветровым напором q_в (z) ( рис. 2.6, б ). 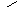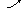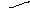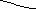При этом над объектом и на его заветренной стороне наблюдается разреже-ние, вызывающее отрицательные давления и . Все эти компоненты ветровых нагрузок учитываются в расчёте как квазистатические.

а) б)

q_в (z)

Рис. 2.6

Интенсивность ветрового напора на высоте z определяется в зависимости от плотности воздуха  , скорости ветра v_в (z) и аэродинамического коэффициента ( лобового сопротивления ) с_х , зависящего от формы здания в плане:

q_в (z) = с_х q₀ (z), где q₀ (z) = 0,5( Па ). ( 2.2 )

Распределение скоростей ветра и ветровых нагрузок по высоте зависит от свойств территории в месте расположения со-оружения ( свободная, застроенная, покрытая деревьями и др. ). Скорости ветра на высотах 10 м и 300 м от поверхности земли

отличаются примерно враза, тогда q_в (300 м)3 q_в (10 м).

Для сооружений с периодами собственных колебаний более 0,25 с действую-щие нормы расчёта строительных конструкций предписывают добавлять к описанной выше так называемой статической составляющей ветровой нагрузки также динами-ческую компоненту, которая в действительности таковой не является, а представляет собой пульсационную составляющую ветрового напора со статистически средним пе-риодом порывов примерно 1 мин ( по энергетическому спектру Давенпорта ). В таком подходе к учёту ветровых воздействий динамические свойства сооружения, которое рассматривается как достаточно жёсткое, по существу, игнорируются.

Для крупногабаритных сооружений ( большепролётных, высотных ) правильное определение сил взаимодействия дефор-мируемого объекта и обтекающего его воздуха возможно только при совместном рассмотрении системы «сооружение – ветровой поток» с использованием в математической модели задачи урав-нений динамики упруго деформируемых систем совместно с уравнениями аэродинамики. Решение такого рода задач состав-ляет предмет аэроупругости. Для объектов сложной конфигу-рации и структуры выполнение расчётов в такой постановке возможно только численными методами с применением совре-менных средств компьютерного физико-математического и ин-женерого анализа – универсальных программных комплексов ( ANSYS, CivilFEM, NASTRAN, MicroFе и др.).

а) б)

В некоторых случаях поведения зданий и сооружений в набегающем ветровом потоке могут быть обнаружены аналогии с движением летательного аппарата в воздушной среде. Напри-мер, поперечные сечения балок большепролётных, особенно ви-сячих, мостов развиты в горизонтальном направлении и прояв-ляют качественное сходство с крылом самолёта – воздействие на него воздушной среды характеризуется лобовым сопротив-лением, подъёмной силой и т. п. При самой простой модели объ-екта такого рода в виде пластин-

ки, плавно обтекаемой потоком па-

р



аллельно срединной плоскости

( рис. 2.7, а ) или под некоторым

у

Рис. 2.7

глом атаки  ( рис. 2.7, б ), при

определённой скорости ветра, на-

зываемой критической, выявляется потеря устойчивости рав-новесия пластинки в потоке воздуха. В зависимости от собствен-ных характеристик конструкции ( размеров пластинки и жёстко-стей связей ) возможны два случая динамического процесса, аль-тернативного исходному равновесию: либо в форме колебаний ( изгибно-крутильный флаттер – от англ. flutter – трепетать ), либо с быстро нарастающим отклонением вследствие исчерпания сопротивления пластинки нарастающему повороту ( скручива-нию ) – дивергенция ( от лат. divergere – отклоняться ). Для обоих случаев существуют формулы вычисления критических скорос-тей ветра через геометрические и жесткостные параметры плас-тинки и её упругих связей.

Но для большинства строительных объектов характерны

н

z

 (t)

едостаточно обтекаемые формы, при которых ламинарное об-текание их воздухом ( дающее квазистатическое напряжённо-деформированное состояние упругой системы ) не реализуется даже при малых скоростях ветра. Возника-

ющие завихрения потока ( турбулентности ) а)

придают процессу динамический характер

к

q_К (z, t)

олебаний, происходящих не только в на-

правлении потока, но и перпендикулярно

ему. Принципиальная схема явления дана

н

y

а рис. 2.8 в применении к высотному объ-

е

x

кту ( многоэтажному зданию, опоре ЛЭП,

башне, мачте и др.), изображённому на

рис. 2.8, а условно в виде консольного сте-

ржня, на который ветер действует вдоль

о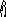си х. С заветренной стороны возникают б)

завихрения потока, причём образующиеся

вихри срываются с поверхности объекта

или угловых точек его сечения ( рис. 2.8, б )

с определённой периодичностью, поочерёд-

н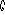о^*) с одной и другой стороны, выстраива-

я

y

сь в так называемую вихревую дорожку

Кармана ( Th. von Karman, 1881 – 1963 ).

 (t)

Отрывающиеся противоположно на-

правленные вихри возбуждают знакопере-

менные нагрузки q_х (z, t) ( в направлении

d

^*) При симметричном сечении на малых скорос-

Рис. 2.8

тях ветра возможно симметричное вихреобра-

зование, но это не представляет опасности.

вдоль ветрового потока – она суммируется с ветровым напором q_в (z) ) и поперечную q_К (z, t) ( рис. 1.60, а ), интенсивность кото-рой можно описать формулой

q_К (z, t) = q_К (z) sin [_К (z) t] , ( 2.3 )

где q_К (z) = 0,5 c_y d; _К (z) = 2 n_К (z) ; n_К (z) = Sh ∙ v_в (z) / d ( Гц )

– частота срыва вихрей; Sh = 0,1 … 0,3 – число Струхаля;

c_y – аэродинамический коэффициент в направлении оси у.

Нагрузка q_х (z, t) изменяется по тому же закону sin [_К (z) t]. Возникают также скручивающие моменты. Частота срыва вих-рей и, соответственно, все аэродинамические нагрузки перемен-ны по высоте, но наибольшее влияние оказывают действующие выше 1/3 высоты Н объекта, где скорости ветра почти вырав-ниваются. Поэтому вызываемые ими пространственные ( изгиб-но-крутильные ) колебания происходят как почти гармонические с частотой _К (H). Такое явление аэроупругости называется срывным флаттером. Оно может не представлять опасности, если учтено в динамическом расчёте. Но при совпадении часто-ты флаттера, зависящей от скорости ветра, с частотой собствен-ных колебаний деформируемой системы возникает ветровой резонанс, при котором в случае слабых демпфирующих свойств сооружения возможно возникновение недопустимо больших пе-ремещений и усилий. Особенно опасен флаттер для сооружений и конструкций, гибких в направлении, перепендикулярном к ветровому потоку, например, для висячих и большепролётных балочных мостов, в которых возможно возникновение верти-кальных ( в плоскости меньшей жёсткости пролётного строения ) и крутильных аэроколебаний, что должно быть предусмотрено динамическим расчётом. Заметим, что скорость воздушного потока и аэродинамические нагрузки практически постоянны по длине моста.

Ещё одно опасное явление аэроупругости – галопирование, механизм которого более сложен и связан с изменениями дина-мических, в том числе демпфирующих, свойств сооружения в процессе движения. Колебания при галопировании, возникаю-щие при превышении скоростью ветра критического значения, нарастают, в отличие от ветрового резонанса, без стабилизации амплитуд, что может привести к разрушению.

Приведённые выше качественные представления и форму-лы следует рассматривать лишь как приближённые модели до-статочно сложных процессов. Динамические расчёты ответст-венных инженерных систем ( зданий, сооружений, конструкций ) должны выполняться, как уже отмечалось, с применением ком-пьютерно реализуемых численных решений, детально и физи-чески корректно описывающих явления аэроупругости, к числу которых, кроме упомянутых выше, относятся воздействия воз-душных ударных взрывных волн, звуковых ударов от сверхзву-ковых самолётов и т. п.