1.7. О приближённом определении частот

собственных колебаний

В динамических расчётах сооружений и конструкций бы- вает полезной упрощённая приближённая оценка частот собст-венных колебаний, в первую очередь – минимальной. Это нуж-но и для ориентировочного прогноза опасности резонанса, и для выбора диапазона поиска в итерационных процедурах определе-ния собственных частот, и для оценки достоверности результа-

^*) Напомним, что учёт сдвига не изменяет числа степеней свободы масс.

тов полного, в том числе компьютерного, расчёта.

В основных способах приближённого вычисления частот собственных колебаний используются:

– априорное описание главной формы, для которой нужно дать оценку частоты колебаний;

– некоторые математические свойства задачи о собственных зна-чениях матриц динамической податливости и жёсткости системы;

– энергетический метод.

В первом случае, исходя из тех или иных качественных со-ображений, аналогий или экспериментальных данных, ожидае-мая форма колебаний приближённо описывается задаваемым

собственным вектором перемещений масс _y = [ _y1 _y2 … _yn ]^т , где некоторый компонент _yi принимается равным 1, а осталь-

ным приписываются конкретные числовые значения, при кото-рых отклонения масс и соответствующие деформации системы с возможно большей достоверностью «напоминают» ожидаемую главную форму. Задание, хотя и приближённое, собственного

вектора _y формально означает, что перемещение y_i определяет все перемещения y = _y y_i, т. е. система может рассматриваться как имеющая одну степень свободы масс.

Если матрица масс диагональная, то i-е уравнение из табл. 1.5 после деления на принимает вид

– 1 = 0, откуда 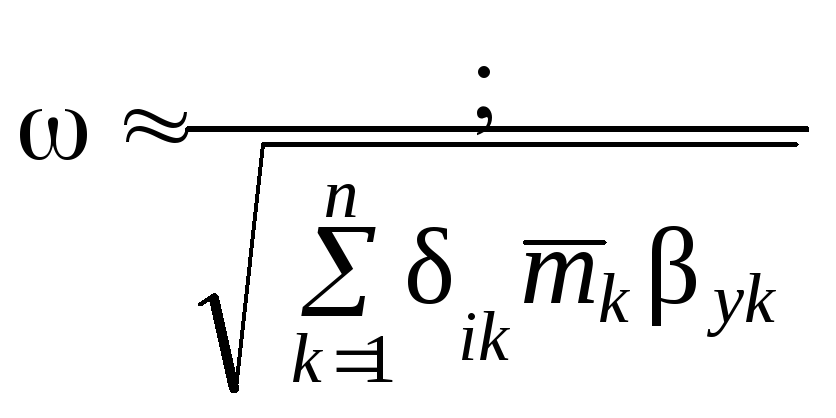. ( 1.142 )

Симметричная балка с защемлёнными концами имеет гла-вную форму колебаний с минимальной частотой, изображённую на рис. 1.51. Её можно приближённо описать уравнением проги-

б

2m

ов, вызванных равномерно распреде-

л

m

m

y₁

y₂

y₃

ённой нагрузкой, в виде полинома

4

l /4

l /4

l /4

l /4

-й степени: y(x) =

тогда y₁ = y₃ и _y = Рис. 1.51

Вычислив обычным путём единичные перемещения ₂₁ = ₂₃ =

= l³/( 384 EI ) и ₂₂ = l³/( 192 EI ), из ( 1.142 ) находим

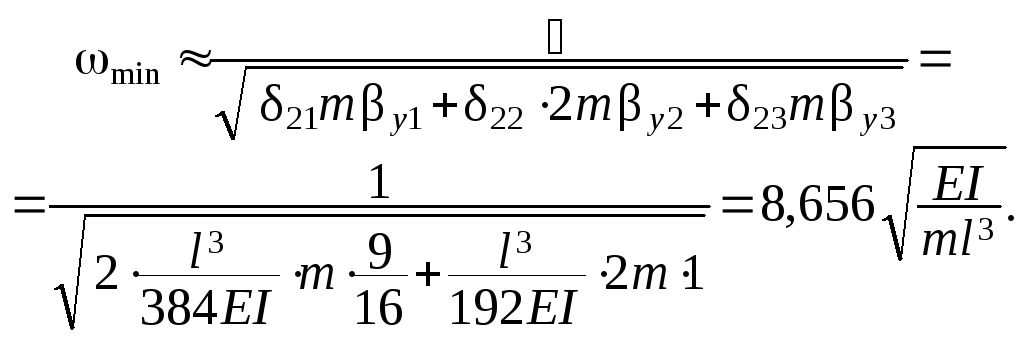
Точное значение – расхождение 0,72 %.

m_n

Для n-этажной рамы можно предсказать форму колебаний по основному тону ( с _min ), для которой характерно доминирова-ние горизонтальных перемещений

(

J_n

J₁

y_n

рис. 1.52 ). Сосредоточивая массы

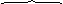
н

m_i

а уровне ригелей рамы и учиты-

в

J_i

ая то, что их перемещения зависят

п

y_i

реимущественно от изгиба колонн,

з

J₂

начительно более гибких, чем ри-

г

y₂

ели, для приближённого описания

деформаций рамы предполагаем

силы инерции ( пропорциональные

массам и перемещениям ) зависящи-

ми от номера этажа i как

J_i = J_n [ 1 – ( 1 – i/n )² ] m_i / m_n .

При n = 4 и одинаковых мас- Рис. 1.52

сах имеем J₁ = 0,438 J_n , J₂ = 0,75 J_n ,

J₃ = 0,938 J_n , J₄ = J_n . Рассчитав раму на эти силы как одновремен-

но приложенные нагрузки ( при любом значении J_n , например, J_n = 1 ), находим вызванные ими перемещения y₁ , …, y_i , …, y_n и затем – вектор _y = [ y₁ / y_i y₂ / y_i … 1 … y_n / y_i ]^т. Одновременно с ука-занным расчётом в матричной форме можно рассмотреть также воздействие J_i = 1 для определения единичных перемещений _ik = _ki ( k = 1, 2, …, n ). Далее – вычисление _min по ( 1.142 ).

Аналогичными по смыслу являются различные варианты приёмов преобразования и замены масс¹.

¹ Киселёв В. А. Строительная механика. Специальный курс. Динамика и устойчивость сооружений : учеб. для вузов / В. А. Киселёв. – 3-е изд., испр. и доп.– М.: Стройиздат, 1980. – 616 с.

Ко второму способу приближённого определения мини-мальной частоты относится формула Донкерлея ( Doncerlay ):

( 1.143 )

г

мы с одной массой m_i , совершающей движе-

ние по i-й степени свободы.

де _i = – парциальная частота, определяемая для систе-

Вывод формулы ( 1.143 ) на основе анализа свойств частот собственных колебаний дан в ² .

Иная форма записи ( 1.143 ):

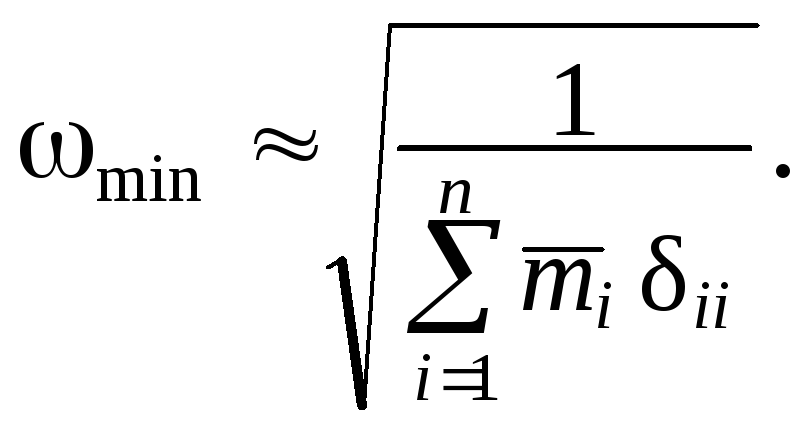( 1.144 )

Для балки по рис.1.51: ₁₁ = ₃₃ = 9l³/( 4096 EI );

–

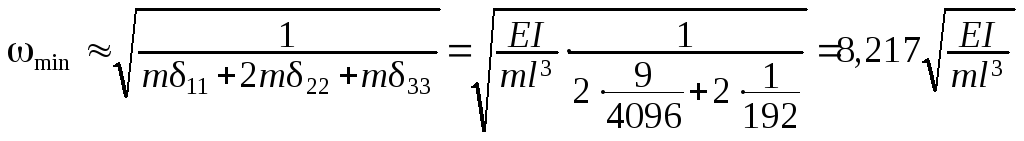погрешность 5,75 %.

Непосредственное практическое применение в динамичес-ких расчётах систем с сосредоточенными массами способов, ре-ализующих энергетический метод, сопряжено с зачастую неоп-равданными математическими трудностями. Современная об-ласть использования энергетического метода в динамике – по-строение теоретических решений новых задач, в том числе в нелинейных постановках, а в прикладном плане – развитие метода конечных элементов ( расширение спектра КЭ, новые расчётные модели ).

² Филин А. П. Прикладная механика деформируемого твёрдого тела. Сопротивление материалов с элементами теории сплошных сред и стро-ительной механики. Т. 3 / А. П. Филин. – М.: Наука. Гл. ред. физ.-мат. литературы, 1981. – 481 с.