1.5.4.4. Расчёт на собственные колебания

по уравнениям в форме метода перемещений

Уравнения ( 1.49 ) в амплитудах перемещений масс и с мат-рицей жёсткости системы в матричной форме записываются как

. . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . .

( 1.65 )

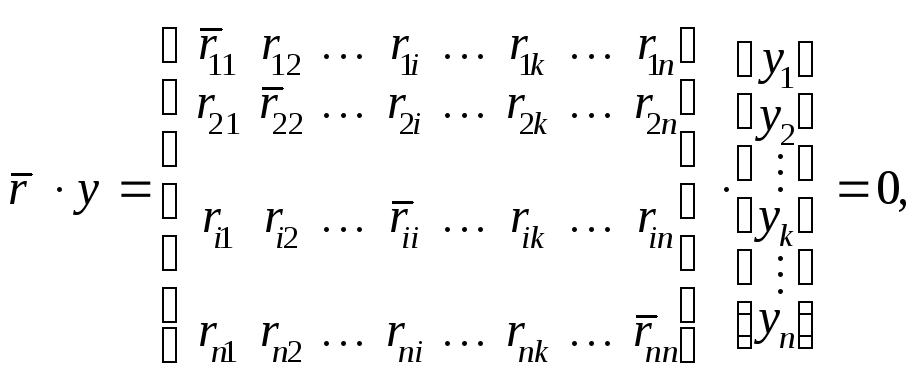
где – матрица динамической жёсткости заданной системы

по направлениям степеней свободы масс при собственных

колебаниях с частотой  :

r – m₀ ² a r –  a ; ( 1.66 )

a – то же, что в формуле ( 1.52 );  = m₀ ² ( для краткости ис-пользовано обозначение  для величины, названной ₀ на с. 14 ).

Матрица единичных реакций r ( внешней жёсткости по на- правлениям степеней свободы масс ) может вычисляться как об-

ратная матрице податливости, т. е. r =  ^–1, либо от единичных

смещений y_i = 1 связей, наложенных на массы по напра-

влениям их возможных перемещений ( см. рис. 1.19 ).

Н

Определение числа степеней

свободы масс n

Число n можно определять как минима-льно возможное число простых связей ( линейных и угловых ), которые нужно наложить на массы системы, чтобы устранить их возможные перемещения.

Выбор основных неизвестных J

и формирование расчетной схемы

На расчетной схеме обозначаются амп-литуды перемещений масс и сил инер-ции.

Запись канонических уравнений

  J = 0 в символьной форме

Число уравнений – n; в диагональных компонентах ( 1.53 ) матрицы  следует раскрыть смысл величин m_i.

Рассмотрение единичных состояний заданной системы при J_i =1, i =1,…,n, с определением силовых факторов

S_i , необходимых для вычисления компонентов матрицы 

Для расчета статически неопредели-мой системы на единичные воздейст-вия J_i =1, которые рассматриваются как варианты загружения, выбирается ра-циональный метод – сил, перемещений или смешанный.

Целесообразно использование ЭВМ.

Вычисление единичных перемеще-

ний _ik и формирование из них

матрицы упругой податливости 

заданной системы

Перемещения в заданной системе мо-гут определяться методом Максвелла – Мора ( или любым другим ) в обычной ( «перемножением» эпюр ) или матрич-ной форме, аналитически или числен-но, в том числе с помощью ЭВМ.

Получение уравнения частот

Det () = 0, отыскание его корней _j

( j = 1,..., n ), определение спектра

частот собственных колебаний _j

( j = 1, ..., n )

Нахождение корней частотного уравне-ния и собственных векторов может выполняться либо прямым решением уравнения n-го порядка с последующим использованием уравнений ( 1.56 ) и за-висимостей ( 1.58 ), либо на ЭВМ по специализированным программам или ППП линейной алгебры.

Вычисление собственных векторов

_J(j) и _y(j) для всех главных форм

колебаний ( j = 1, ..., n )

Проверки ортогональности

главных форм по (1.60 )

Не выпол-

няются

При необходимости уточнения схемы деформаций в какой-либо главной форме определяется нужное число перемещений разных точек системы от воздействий J_i = _Ji J_k ( i = 1, ..., n ).

Выполняются

Изображение схем деформаций си-

стемы в главных формах колебаний

Качественная оценка

правдоподобия

полученных главных форм

Обнаружены

противоречия

главных форм

Формы правдоподобны

особенностям Результат

заданной системы отрицательный

Вычисление динамических

силовых факторов по ( 1.64 )

Статическая и кинематическая

проверки – с. 59, ф-ла ( 1.63 )

К

Результат

положительный

Рис. 1.25

Матрица как обобщённая характеристика динамических свойств системы играет в данном варианте расчёта ( в форме ме-тода перемещений ) ту же роль, что матрица податливости в расчёте в форме метода сил ( см. с. 54 ). Диагональные компонен-ты матрицы содержат динамические поправки:

= r_ii – ² r_ii – a_i . ( 1.67 )

Умножением на a ^–1 уравнения ( 1.65 ) приводятся к виду B –= 0, т. е. к стандартной задаче о собственных значениях

матрицы B = математически решаемой так же, как в рас-

смотренном ранее варианте с матрицейи неизвестными J: не-тривиальное решение при y  0 ( условие существования колеба-ний ) даёт характеристическое ( частотное ) уравнение:

DetDet ( r –  a )

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

( 1.68 )

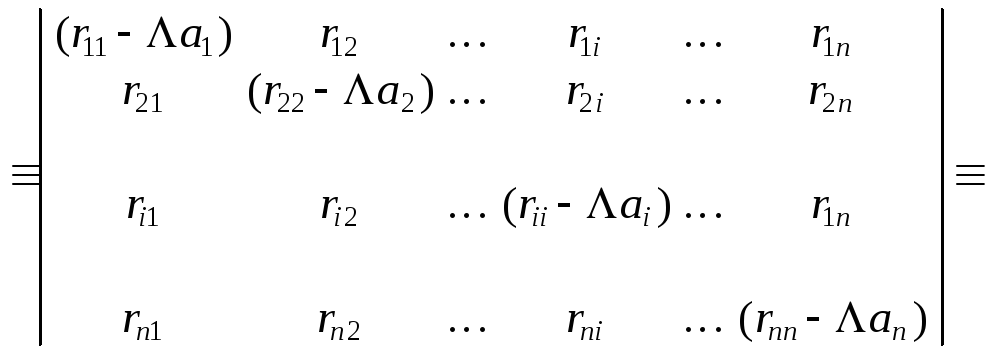
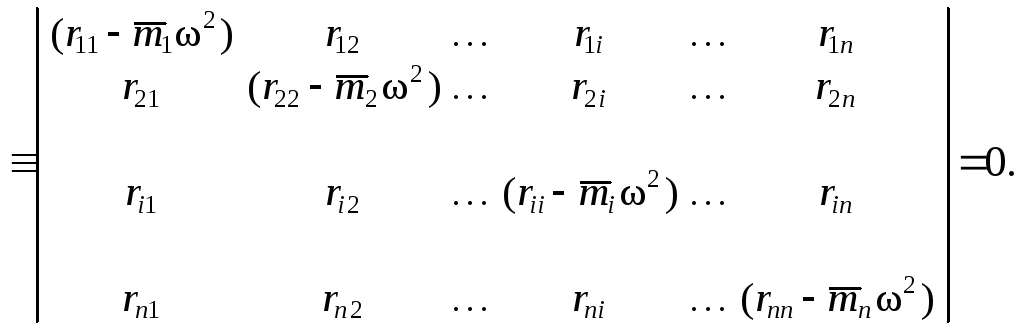
Найденные корни уравнения ( 1.68 ) ₁ , ₂ , …, _j , …, _n используются для вычисления собственных частот _j = ( j = 1, 2, ..., n ).

Далее для каждого значения частоты _j определяется соответствующий собственный вектор основных неизвестных _{y( j )} = – решением редуцированной системы уравнений

_{y(j), red} + = 0 ( 1.69 )

и

ли

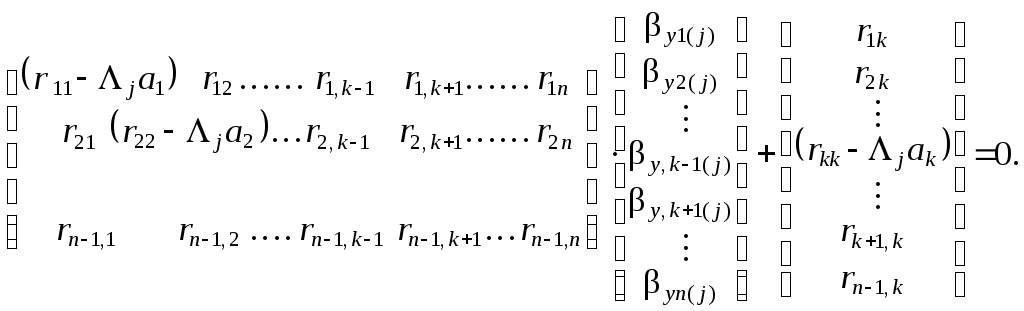
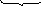
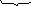
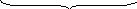
(1.69*)

По вектору _{y( j )} вычисляется собственный вектор инерци-онных сил _y(j) = a _J(j) , ( 1.70 )

после чего заключительный этап – проверка результатов расчё-та – выполняется по методике, изложенной на с. 59 – 60.

Весь расчёт на собственные колебания по уравнениям в форме метода перемещений производится по тому же алгоритму, что и в варианте в форме метода сил ( рис. 1.25 ) – следует лишь заменить в нём J на y,  на r.

Для компьютерной реализации, в том числе в форме мето-да конечных элементов, наиболее приспособлен подход, осно-ванный на формировании уравнений динамики для расчётной модели, по смыслу представляющей собой основную систему классического метода перемещений ( ОСМП ), где в качестве основных неизвестных Z принимаются перемещения расчётных узлов ( в динамической задаче о собственных колебаниях Z – амплитуды перемещений ). В этом подходе особенностью ОСМП в динамике является то, что кроме расчётных узлов, назначае-мых по правилам метода перемещений, использовавшимся ранее для случаев статических воздействий, в число расчётных узлов включаются также точки расположения масс. При этом часть

основных неизвестных Z – суть перемещения масс y_i ( ) по

направлениям их степеней свободы. Полный вектор перемеще-

ний Z представляется состоящим из двух частей: Z = [] ^т ,

где Z_mу – вектор амплитуд компонентов перемещений масс; Z_d – вектор перемещений, не являющихся степенями свободы масс. Число компонентов вектора Z_m = у равно n, количество пе-ремещений Z_d обозначим n_d , тогда общее число неизвестных Z будет n₀ = n + n_d . Система статических уравнений метода пере-мещений R_{0, i} = 0 ( ) состоит из двух групп, выражающих:

1

d_k

J_{i +1}

R_{0, dk}

) отрицание полных реакций допол-

н

J_i

ительных связей, наложенных на рас-

ч

i +1

i

R_{0, i}

ётные узлы с массами ( рис. 1.26 ) и

непосредственно воспринимающих в

О

R_{0, i +1}

СМП инерционные силовые факторы

J

Рис. 1.26

_i ( ): R_{0, i} = R_{0, iZ} + R_{0, iJ} =

=; ( 1.71 )

2) отрицание полных реакций всех остальных дополнительных связей в расчётных узлах:

R_{0, i} = R_{0, iZ} = ( 1.72 )

Система канонических уравнений в матричной форме:

( 1.73 )

где – матрица динамической жёсткости выбранной основной

системы метода перемещений;

r_{0, yy} – матрица реакций дополнительных связей в ОСМП по

направлениям степеней свободы масс, от их единичных

смещений ( от Z_mi = 1, );

r_{0, yd} – матрица реакций дополнительных связей в ОСМП по

направлениям степеней свободы масс, от единичных

смещений других связей по направлениям, не совпада-

ющим со степенями свободы масс ( от Z_dk = 1, );

r_{0, dy} – матрица реакций связей в расчётных узлах ОСМП по

направлениям, не совпадающим со степенями свободы

масс, от единичных смещений связей по направлениям

степеней свободы масс ( от Z_mi = 1, ); r_{0, dy} = .

r_{0, dy} – матрица реакций связей в расчётных узлах ОСМП по

направлениям, не совпадающим со степенями свободы

– матрица ( n x n ) приведённых масс.

масс, от их единичных смещений ( от Z_dk = 1, );

Если ввести в рассмотрение расширенную матрицу масс

( 1.74 )

, то уравнения ( 1.73 ) можно представить как

г

темы МП по направлениям всех неизвест-

ных Z = [] ^т .

де – матрица внешней жёсткости основной сис-

Вычисление r₀ возможно любыми известными способами – статическими и кинематическими, в том числе через матрицу внутренней жесткости K₀ по формуле r₀ = a_e^т K₀ a_e ( здесь а_e – матрица смещений узлов элементов ОСМП, в собственных ло-кальных осях, от единичных основных неизвестных Z; K₀ – блоч-ная диагональная матрица, формируемая из стандартных матриц жёсткости для элементов определённых типов ).

Вводя, как обычно, в рассмотрение собственное число  = m₀ ² , представляем уравнения ( 1.74 ) в виде

( 1.75 )

где

Частотное уравнение получается как результат постанов-ки условия существования колебаний Z  0 – нетривиальное ре-шение однородной системы ( 1.74 ):

( 1.76 )

Независимо от общего числа n₀ перемещений Z порядок алгебраического характеристического уравнения ( 1.76 ) равен числу степеней свободы масс n , так как собственное число ,

связанное с частотой , присутствует только в блоке ( n x n )

матрицы.

Из уравнений ( 1.73 ) формально математическим путём мо-гут быть получены уравнения собственных колебаний ( 1.65 ), т. е.из табл. 1.5, относящиеся не к ОСМП, а к заданной систе-ме. Это можно истолковывать как применение кинематически неопределимой основной системы с расчётными узлами только в точках расположения масс и с неполным их закреплением – лишь связями по направлениям независимых возможных пере-мещений масс, т. е. с расчётной моделью по рис. 1.20 ( при от-сутствии заданных воздействий ). Для указанного преобразова-ния из второй группы уравнений ( 1.73 ) неизвестные Z_d вы-ражаются через главные неизвестные – перемещения масс y :

Z_d = – Подстановка этого выражения в первую груп-пу уравнений ( 1.73 ) даёт систему из

которой следует формула для вычисления матрицы динами-ческой жёсткости заданной системы:

( 1.77 )

с переходом к уравнению частот собственных колебаний