
- •Основные положения теории динамических расчётов деформируемых систем с конечным числом степеней свободы масс
- •1.1. Термины, понятия и определения
- •1.2. Основные символы и обозначения
- •1.3. Предпосылки и гипотезы динамического расчёта. Принципиальная расчётная модель деформируемой системы с сосредоточенными массами
- •1.4. Степени свободы масс
- •1.5. Уравнения динамики деформируемых систем с конечным числом степеней свободы масс
- •1.5.1. Уравнения для общего случая движения
- •1.5.1.1. Использование матрицы податливости системы
- •1.5.1.2. Уравнения движения с матрицей жёсткости системы
- •1.5.2. Систематизация и анализ вариантов уравнений динамики
- •1.5.3. О численном решении уравнений динамики систем с конечным числом степеней свободы масс
- •1.5.4. Свободное движение и собственные колебания
- •1.5.4.1. Уравнения свободного движения, их решение;
- •1.5.4.2. Характеристическое ( частотное ) уравнение;
- •Дополнительные сведения о собственных векторах j и y
- •1.5.4.4. Расчёт на собственные колебания
- •1.5.5. Вынужденное движение; установившиеся колебания от вибрационных воздействий
- •1.6. Обобщённые перемещения, группировка неизвестных и учет симметрии в динамических расчётах
- •1.7. О приближённом определении частот
- •2. Некоторые инженерные приложения динамики систем с конечным числом степеней свободы масс
- •2.1. Кинематическое возбуждение движения деформируемой системы. Понятие о расчёте на сейсмические воздействия
- •2.2. Понятие об аэроупругости и расчётах сооружений на ветровые нагрузки
- •2.3. Защита сооружений и конструкций от динамических воздействий
- •3. Примеры динамических расчётов статически неопределимых стержневых систем с сосредоточенными массами
- •Задача 3.1. Расчёт плоской стержневой системы на собственные и вынужденные колебания
- •3.1.1. Динамический расчёт рамы
1.5.4. Свободное движение и собственные колебания
Само по себе свободное движение сооружения или конст-рукции в отсутствие динамических нагрузок или кинематичес-ких возмущений практического интереса, как правило, не пред-ставляет. Исследование его бывает необходимо для определения начальных условий движения в момент возобновления воздей-ствия, когда полного затухания ранее возбуждённых свободных колебаний ещё не произошло.
1.5.4.1. Уравнения свободного движения, их решение;
случай собственных колебаний
Уравнения для общего случая свободного движения ( с учё-том затухания вследствие диссипации энергии ) приведены в табл. 1.4. В варианте 10А0 – в перемещениях и с использованием матрицы податливости системы развёрнутый вид этих уравне-ний таков:
. . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
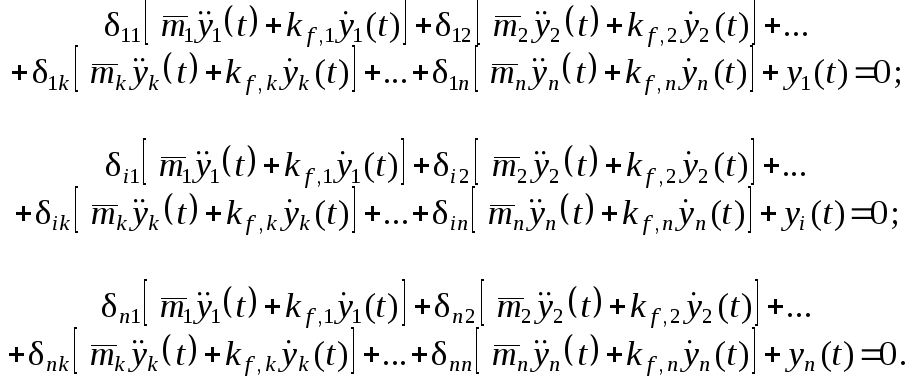
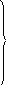
С матрицей жёсткости ( 10Б0 ):
. . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .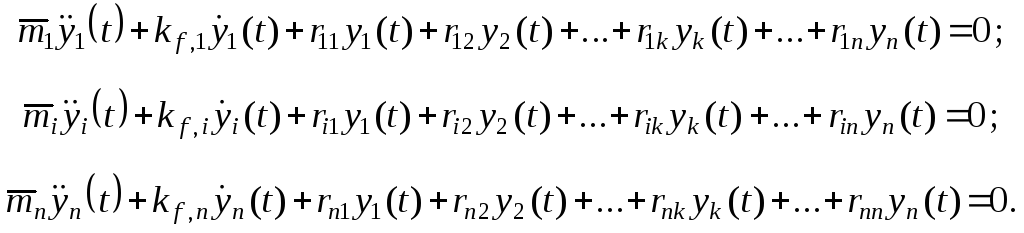
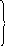
Общее решение систем однородных дифференциальных уравнений может быть представлено в виде [ 1 ] :
yi
(t)
=![]() (
1.45
)
(
1.45
)
о
yij
(t)
Tj
Tj
к омбинациями
затухающих гар-
омбинациями
затухающих гар-
м
Aij
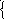



н t



Aij
небрежимо малом рассеянии
энергии ( j = 0, j = 1, 2, …, n ) Рис. 1.22
yi
(t)
=![]() ( 1.46
)
–
незатухающее
полигармони-
( 1.46
)
–
незатухающее
полигармони-
ческое движение по направлению i-й степени свободы.
Для определения
начальных амплитуд Aij
и фаз 0j
состав-ляются и решаются 2n
уравнений, выражающих начальные ус-ловия
движения (
в перемещениях
yi
(0) и
скоростях![]() )
всех масс, а
угловые частоты j
находятся решением особого урав-нения,
смысл которого будет раскрыт в п. 1.5.4.2.
)
всех масс, а
угловые частоты j
находятся решением особого урав-нения,
смысл которого будет раскрыт в п. 1.5.4.2.
Особое значение в динамическом расчёте сооружения ( кон-струкции ) имеет рассмотрение частного случая свободного дви-жения – собственных колебаний, при которых, по определению ( см. с. 11 ), все массы движутся синфазно моногармонически, с образованием незатухающих стоячих волн перемещений и де-формаций, описываемых условием ( 1.1 ). Собственные колеба-ния, в точном смысле, возможны лишь в консервативных ( иде-альных ) системах при строго определённом задании начальных условий движения масс. Несмотря на это, расчёты на собствен-ные колебания актуальны и для реальных систем – при этом в подавляющем большинстве случаев пренебрегают диссипатив-ными факторами, поскольку их влияние на частоты и формы ко-лебаний сооружений и строительных конструкций в большин-стве случаев незначительно ( см. с. 44 ).
Заметим, что есть методы определения собственных частот с учётом диссипа-ции ( в частности, с использованием обобщённых комплексных характеристик упругости материала [ 1 ] ) , так как иногда игнорировать её влияние нельзя, например, для под-земных сооружений в водонасыщеных вязких грунтах. Нужно также знать, что даже будучи несущественным для низкочастотных форм собственных колебаний, рассеяние энергии может сказываться в большей степени в высокочастотных колебаниях, и тогда не следует пренебрегать им при нахождении соответстствующих частот и главных форм.
Запишем в развёрнутом виде все варианты уравнений соб-ственных колебаний консервативной линейно деформируемой системы с конечным числом степеней свободы масс, согласно табл. 1.5.
С использованием матрицы податливости заданной
системы:
![]() – в
амплитудах
перемещений масс
(
в каждом
уравне-
– в
амплитудах
перемещений масс
(
в каждом
уравне-
нии объединены по
два слагаемых, содержащих yi
с номером уравнения;
все члены
разделены на 2![]() ):
):
. . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . .
. . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . .
(
1.47
)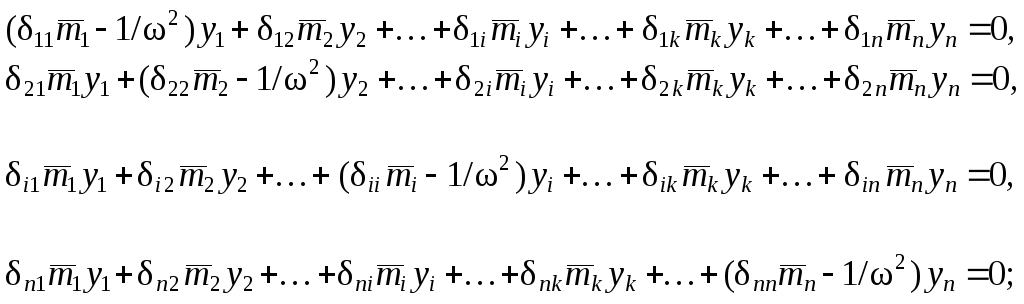
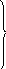
![]() – в амплитудах
инерционных
силовых
факторов
– в амплитудах
инерционных
силовых
факторов
( с объединением слагаемых, содержащих Ji в i-м уравнении ):
. . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
.
. . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .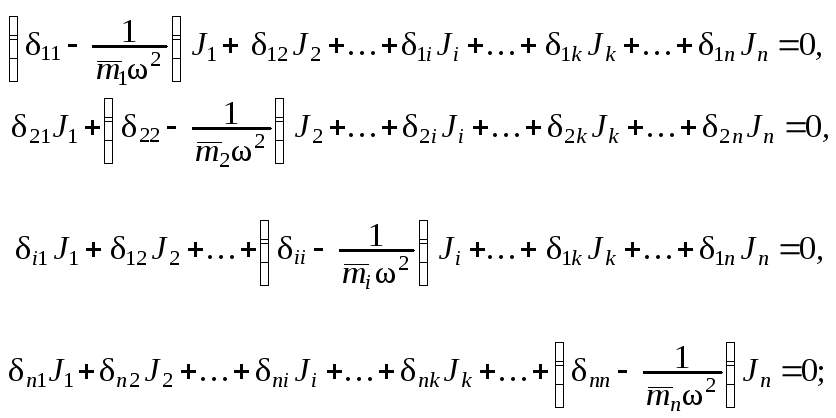
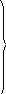 ( 1.48
)
( 1.48
)
С использованием матрицы жёсткости заданной системы:
![]() – в
амплитудах
перемещений масс:
– в
амплитудах
перемещений масс:
. . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .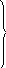
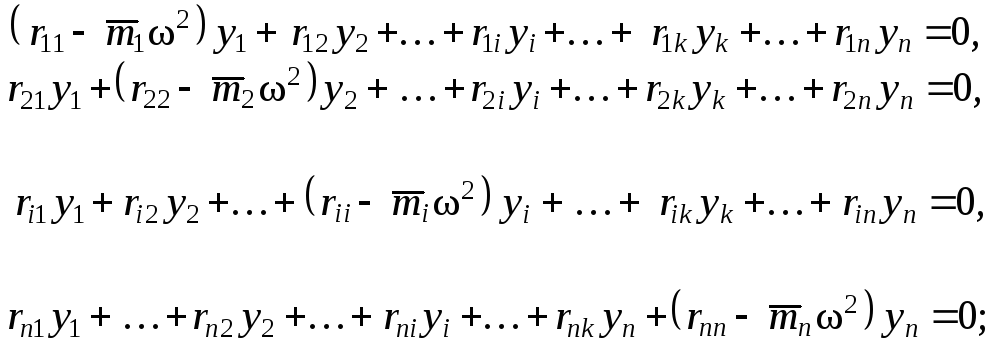 ( 1.49
)
( 1.49
)
![]() – в
амплитудах
инерционных
силовых
факторов:
– в
амплитудах
инерционных
силовых
факторов:
. . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
вестными – (
1.47
) и (
1.49
), (
1.48
) и (
1.50
)
–
видно,
что наибо-
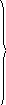
Из сравнения уравнений в вариантах с одинаковыми неиз-
лее компактными ( содержащими характеристики инертности системы – приведённые массы – только в n диагональных коэф-фициентах при неизвестных ) являются:
– при использовании амплитуд сил инерции масс в качестве не-известных – ( 1.48 );
– в амплитудах перемещений масс – ( 1.49 ).
Матричная запись уравнений ( 1.48 ):
. . . . . . . . . . . . . . .
. . . . . . .
. . . . . . . . . . . . . . .
. . . . . . .
y3
Jn
–
1
J1
с
y1
Jn
J3

д
yn
–
1
J2












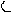
и
yn
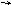

с
y2
yi
yk

р
Jk
Ji
л

 юбую
линейно
деформи-
юбую
линейно
деформи-
руемую систему.
Рис. 1.23




потезами и предпосылка-
ми линейной теории динамики сооружений ( см. с. 15 ), а также смыслом уравнений ( 1.51 ), система рассматривается в состоя-нии амплитудного отклонения от исходного положения стати-ческого равновесия, обозначенного штриховыми линиями как условно недеформированное. Согласно выводу, сделанному на с. 41, амплитуды инерционных силовых факторов и соответст-вующих им перемещений показаны совпадающими по направле-ниям.
Напомним, что систему можно было бы представлять как невесомую, без масс, которые сохранены в расчётной схеме лишь как указание на источник возникновения д’аламберовых инерционных сил. Кроме пренебрежения дис-сипацией энергии, никаких ограничений – ни по типу системы ( плоская или про-странственная, стержневая, пластинчато-оболочечная или континуальная ), ни по виду её напряжённо-деформированного состояния, ни по характеру связей ( дис-кретные или распределенные типа упругого основания ) – не вводится.
Цель расчета – определение частот собственных колеба-ний системы и выявление соответствующих им главных форм колебаний.
Как следует из соображений, приведённых в пп. 1.5.1 и 1.5.2, уравнения ( 1.51 ) ( иногда называемые, по внешнему сход-ству с уравнениями классического метода сил, каноническими уравнениями собственных колебаний ) выражают амплитуды y перемещений масс через амплитуды J инерционных силовых факторов.
Матрица
коэффициентов
![]() уравнений ( 1.51 ) называется матрицей
динамической податливости
заданной системы
по направлениям сил
инерции.
Она
выражается
через
матрицу
упру-гой податливости
,
матрицу относительных масс a
и частоту собственных
колебаний
(
или
связанное
с
ней
собственное
число
):
уравнений ( 1.51 ) называется матрицей
динамической податливости
заданной системы
по направлениям сил
инерции.
Она
выражается
через
матрицу
упру-гой податливости
,
матрицу относительных масс a
и частоту собственных
колебаний
(
или
связанное
с
ней
собственное
число
):
![]() =
–
(
m0
2
)
–1
a
–1
=
–
(
m0
2
)
–1
a
–1
![]()
–
a
–1
, (
1.52
)
–
a
–1
, (
1.52
)
г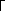
 де
a
=
a1
…
ai
…
an
=
де
a
=
a1
…
ai
…
an
=![]()
=
=![]()
( здесь для краткости символом обозначена величина 0 со с. 14 ).
Динамические
поправки содержатся только в диагональ-ных
компонентах*)
матрицы
![]() :
:
![]() =
ii
–
1/
(
=
ii
–
1/
(![]()
2)
2)
![]() ii
–
/ai
(
ai
=
ii
–
/ai
(
ai
=![]() ),
i
=
1,
2,
...,
n.
(
1.53
)
),
i
=
1,
2,
...,
n.
(
1.53
)
Матрица динамической податливости является обобщён-ной динамической характеристикой линейно деформируемой системы при определённом виде её движения, поскольку содержит в себе данные, количественно описывающие
а) упругие свойства системы – посредством матрицы , учитывающей ее геометрические, структурные и жесткостные особенности;
б) инерционные
качества
системы – через характеристики масс
m0
и a
либо непосредственно![]() ,
а также через выбор опре-делённых (
согласно
степеням свободы масс
) направлений
пере-мещений ik
в матрице упругой податливости ;
,
а также через выбор опре-делённых (
согласно
степеням свободы масс
) направлений
пере-мещений ik
в матрице упругой податливости ;
* )
В дальнейшем будут рассмотрены особые
случаи с недиагональным
)
В дальнейшем будут рассмотрены особые
случаи с недиагональным
расположением днамических поправок.
в) пространственный и временной аспекты движения – посредством частоты , относящейся, по определению, к такому особому случаю движения системы, в котором все её массы син-фазно совершают моногармонические колебания по ( 1.1 ), при-чём конкретному значению ( характеризующему развитие про-цесса во времени ) отвечает определённая главная форма ( про-странственное описание движения ).
