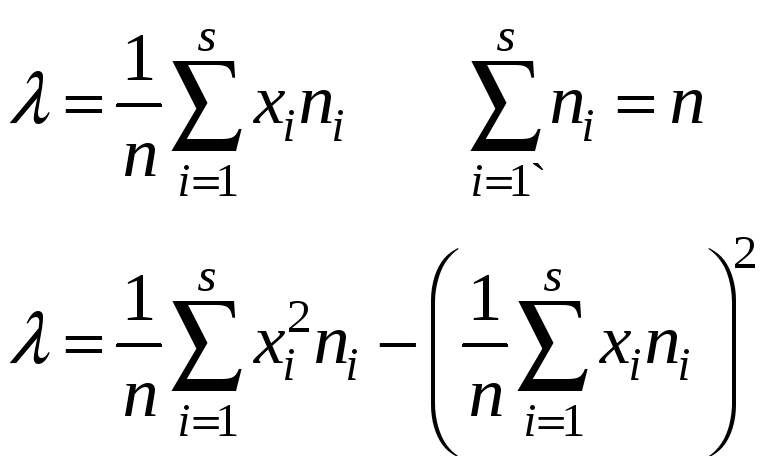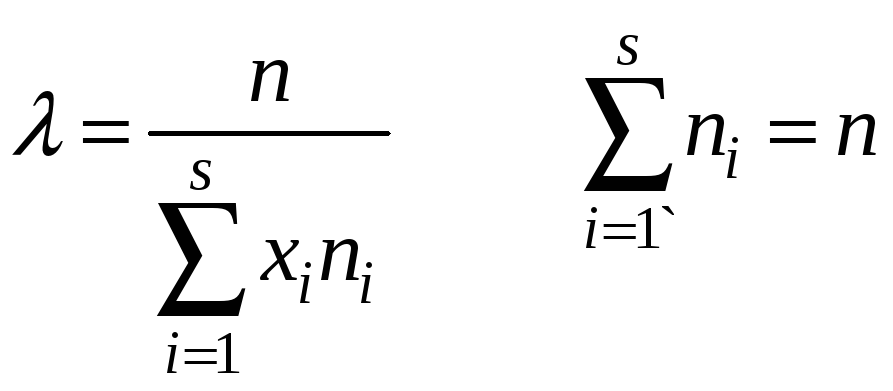1.3.1. Оцінка параметрів закону розподілу

Після вибору відповідного виду розподілу проводиться оцінка його параметрів за допомогою методів максимальної правдоподібності або моментів. Оцінкою параметра називають його наближене значення, побудоване по вибірці спостережень.

У табл.2 представлено оцінки параметрів деяких наведених вище розподілів, що обчислюють по отриманим у результаті експерименту даним.

Таблиця 2

Дискретні і неперервні статистичні розподіли

Тип розподілу	Характеристики розподілу	Оцінка параметрів розподілу за вибірковим даними
Пуассона
Нормальне (Гауса)
Логарифмічно нормальне
Експоненціальне 

Перевага застосування типових законів розподілу складається в їхній добрій вивченості і можливості одержання консистентних, незміщених і ефективних оцінок параметрів.

1.3.1. Приклади побудови деяких законів розподілу

Приклад 1: побудова закону Пуассона за ЕД

Аналізуючи дискретну випадкову величину, для якої можливі значення повинні бути лише послідовними цілими числами, а вибіркові середнє і дисперсія мало відрізняються одне від одного, можна чекати, що ЕД будуть досить точно описуватися законом розподілу Пуассона.

У результаті проведення експерименту – реєстрації кількості значень згасання сигналу на частоті 1000 Гц каналу телефонної мережі – отримано емпіричний варіаційний ряд

	0	1	2	3	4	5	6	7	8	9	10	11	12
	42	156	294	403	410	329	225	157	54	17	8	4	1

Обсяг вибірки становить .

У припущенні про розподіл ознаки за законом Пуассона побудувати теоретичний закон розподілу досліджуваної ознаки.

Розв'язання: для знаходження теоретичного закону треба:

• обчислити вибіркові середнє і дисперсію;

• переконатися в тому, що вони мало відрізняються;

• вибрати як параметр розподілу величину вибіркового середнього ;

• обчислити теоретичні частоти за побудованим розподілом Пуассона.

Досліджувана ознака – кількість значень загасань сигналу – приймає лише послідовні цілочисельні значення.

Обчислимо вибіркові середнє і дисперсію:

Оскільки і приблизно рівні, то ми маємо підстави припустити, що дана вибірка розподілена за законом Пуассона (7) з параметром

, де . (16)

Величина коефіцієнта варіації (15)

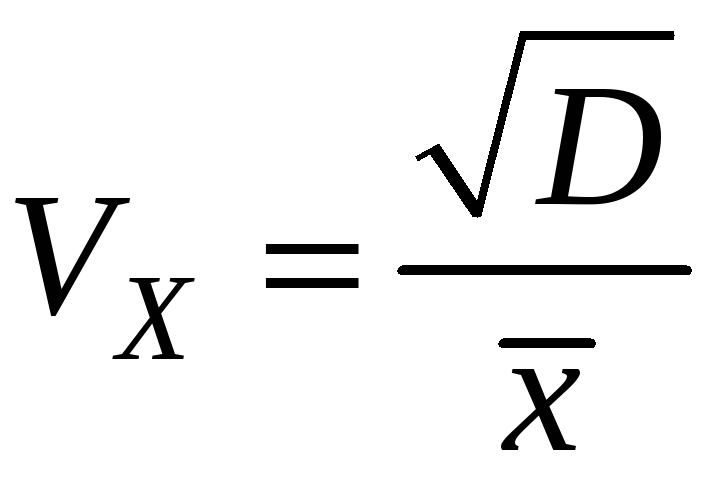
також свідчить про те, що експериментальний розподіл може бути близьким до розподілу Пуассона (див. табл.1).

Обчислимо теоретичні частоти , (нагадаємо, що значення функції Пуассона (7) у випадку (16) знаходять у додатку 1 при ).

Для обчислення теоретичних частот за побудованим законом розподілу зручно розташувати допоміжні розрахунки у вигляді табл.3.

Таблиця 3

Розрахунок теоретичних частот за законом Пуассона

0	0,0183	38,43	38	42
1	0,0733	153,93	154	156
2	0,1465	307,65	308	294
3	0,1954	410,34	410	403
4	0,1954	410,34	410	410
5	0,1563	328,23	328	329
6	0,1042	218,82	219	225
7	0,0595	124,95	125	157
8	0,0298	62,58	63	54
9	0,0132	27,72	28	17
10	0,0053	11,13	11	8
11	0,0019	3,99	4	4
12	0,0006	1,26	2	1
	0,9997		2100	2100

На рис.15 наведено полігони емпіричних і теоретичних частот даного розподілу.

Рис.15 Порівняння теоретичнх і емпіричних частот

Слід зазначити, що сума ймовірностей всіх можливих значень із другого стовпця табл.3 незначно відрізняється від одиниці, а при знаходженні теоретичних частот шляхом округлення величин для останнього значення замість 1 прийнято 2, оскільки сума теоретичних і експериментальних частот повинні збігатися.

Приклад 2: побудова показникового закону за ЕД

На АТС отримано інтервальний розподіл часу обслуговування 60 заявок:

	0–5	5–10	10–15	15–20	20–25	25–30	30–35
	30	16	7	3	2	1	1

Тут – час обслуговування одного клієнта; – кількість клієнтів, які були обслужені за час . Загальна кількість заявок складає обсяг вибірки .

У припущенні про розподіл ознаки за показниковим законом побудувати теоретичний закон розподілу досліджуваної ознаки.

Розв'язання: для обчислення вибіркових середнього і середнього квадратичного відхилення варто спочатку перейти до дискретного розподілу, взявши за можливі значення середини статистичних інтервалів:

	2,5	7,5	12,5	17,5	22,5	27,5	32,5
	30	16	7	3	2	1	1

Для величин середнього і середнього квадратичного відхилення відсутнє повний збіг їхніх значень , але спробуємо все-таки обчислити теоретичні частоти за допомогою показникового закону (12) з параметром

.

Значення коефіцієнта варіації (15)

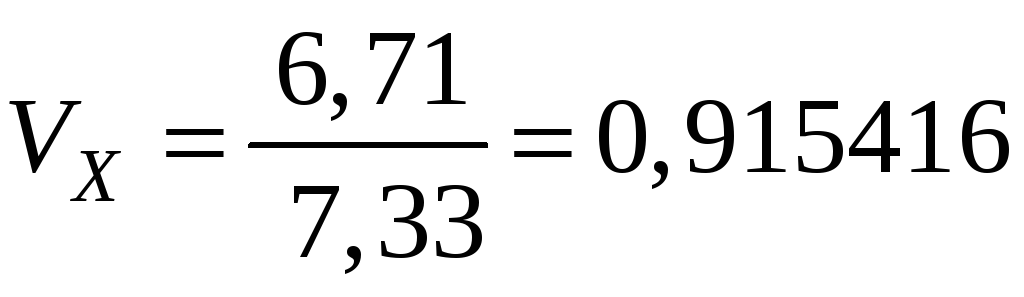
близько до одиниці і тому можна висунути гіпотезу про розподіл ознаки за експоненціальним законом.

Функція і щільність розподілу мають вигляд

(17)

(18)

Теоретичні частоти обчислюємо на основі щільності ймовірності (18) , тут – довжини інтервалів розподілу (див. табл.4).

Таблиця 4

Розрахунок теоретичних частот

2,5	0,0987	29,61	30	30
7,5	0,049	14,7	15	16
12,5	0,0243	7,29	7	7
17,5	0,0121	3,63	4	3
22,5	0,006	1,8	2	2
27,5	0,003	0,9	1	1
32,5	0,0015	0,45	1	1
	0,1946		60	60

Помітимо, що, незважаючи на деяку відмінність значень середнього і середнього квадратичного відхилення, теоретичні і емпіричні частоти майже збігаються (див. рис.16).

Рис.16. Гістограми теоретичних і емпіричних частот

Приклад 3: побудова нормального закону за ЕД за допомогою функції розподілу

ВТК перевірив час обробки (у хвилинах) 200 деталей. У результаті отримано вибірку, яка задана інтервальним розподілом:

	0–2	2–4	4–6	6–8	8–10	10–12	12–14
	2	12	44	92	38	11	1

У припущенні про нормальний розподіл вибіркової сукупності побудувати теоретичний закон досліджуваної ознаки на основі функції розподілу.

Розв'язання: емпіричні частоти влучення в інтервал задано, визначимо теоретичні частоти, припускаючи, що генеральна сукупність розподілена за нормальним законом.

Весь інтервал спостережених значень випадкової величини (вибірки обсягу ) уже розбито на часткових інтервалів однакової довжини. Аналогічно прикладу 2 перейдемо до середин часткових інтервалів:

	1	3	5	7	9	11	13
	2	12	44	92	38	11	1

Обчислимо і .

Значення коефіцієнта варіації свідчить про те, що можна висунути гіпотезу про розподіл ознаки за нормальним законом (див. табл.1).

Параметри розподілу є такими ; , тоді . Теоретична функція розподілу і щільність ймовірності мають вигляд

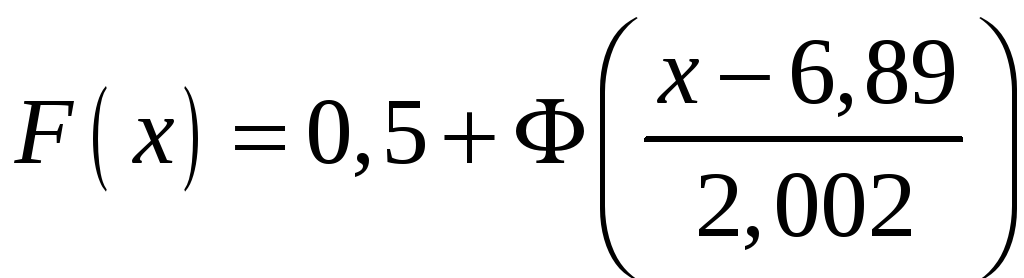, (19)

. (20)

Для побудови теоретичних частот на основі функції розподілу , яка визначається формулою (19), варто спочатку обчислити умовні варіанти і , потім по таблицях (додаток 3), що складено для функції Лапласа , знайти і . Теоретичні частоти визначають за формулою , причому самі значення теоретичних частот зазвичай округляють до цілих чисел, щоб одержати обсяг вибірки . Обчислення зручно представити у вигляді табл.5.

Таблиця 5

Розрахунок теоретичних частот

0–2	2	-2,443	-3,442	-0,4927	-0,4997	1,39	1
2–4	12	-1,444	-2,443	-0,4251	-0,4927	13,52	14
4–6	44	-0,445	-1,444	-0,1736	-0,4251	50,30	50
6–8	92	0,5544	-0,445	0,2088	-0,1736	76,48	77
8–10	38	1,5534	0,5544	0,4394	0,2088	46,12	46
10–12	11	2,5524	1,5534	0,4948	0,4394	11,08	11
12–14	1	3,5514	2,5524	0,4998	0,4948	1,00	1
	200						200

Спостерігається деяка розбіжність емпіричних і теоретичних частот ( рис.17).

Рис.17. Гістограми теоретичних і емпіричних частот

Приклад 4: побудова нормального закону за ЕД за допомогою щільності розподілу

Побудуємо теоретичні частоти для ЭД з прикладу 3, засновуючи розрахунки на отриманому виразі (20) для щільності ймовірності.

Розв'язання: для проведення обчислень варто перейти до середин інтервалів і обчислити умовні варіанти , потім обчислити значення функції для умовних варіант (див. додаток 2). Теоретичні частоти знаходять за формулою , де – обсяг вибірки, – довжина часткових інтервалів. Розрахунки наведено в табл. 6.

Таблиця 6

Розрахунок теоретичних частот

1	2	-2,942	0,00530	1,0589411	1
3	12	-1,943	0,06077	12,141858	12
5	44	-0,944	0,25647	51,242757	51
7	92	0,0549	0,39822	79,564436	79
9	38	1,0539	0,22988	45,93007	46
11	11	2,0529	0,04879	9,7482518	10
13	1	3,0519	0,00381	0,7612388	1
	200				200

На рис.18 показані полігони теоретичних і емпіричних частот даного статистичного розподілу.

Рис.18. Полігони теоретичних і емпіричних частот

Слід зауважити, що у випадку вихідного дискретного статистичного розподілу теоретичні частоти за допомогою щільності ймовірності визначають на основі цього розподілу, а для побудови теоретичних частот за допомогою функції розподілу переходять до інтервального розподілу, середини інтервалів якого збігаються зі значеннями .