1.2. Типові закони розподілу випадкової величини

Найпоширеніші в природі і у суспільному житті випадкові величини розподілені за нормальним законом, а також за біноміальним законом, за законом Пуассона. Зустрічаються випадкові величини, розподілені за законом Максвелла, які мають розподіл або розподіл. У теорії і практиці надійності найчастіше використовуються наступні закони розподілу: нормальний (Гауса), логарифмічно нормальний, Вейбула, експоненціальний (показниковий). Розглянемо деякі закони розподілу, що найбільш часто використовують на практиці економічних і технічних досліджень.

1.2.1. Геометричний розподіл

Геометричний розподіл визначається функцією ймовірності

, (5)

де характеризує число невдач до першого успіху, – імовірність успіху, – імовірність невдачі. Функція ймовірності (див. рис.6) є геометричною прогресією, звідки і походить назва розподілу.

Рис.6. Функція ймовірності геометричного розподілу

Інтегральна функція геометричного розподілу визначається формулою .

Характеристики випадкової величини , що розподілена за геометричним законом (5), є такими: математичне сподівання ; дисперсія ; асиметрія ; ексцес .

1.2.2. Біноміальний розподіл

Найбільш загальним випадком різного роду імовірнісних розподілів є біноміальний розподіл. Нехай випадкова величина визначає число появ деякої події в незалежних випробуваннях. Ймовірність появи події в кожному з них постійна і дорівнює , ймовірність не появи події в окремому випробуванні при цьому дорівнює . Тоді ймовірність того, що випадкова величина прийме значення, що дорівнює , тобто подія з'явитися разів обчислюють за формулою Бернуллі (див. рис.7)

. (6)

Біноміальний розподіл при фіксованому обсязі вибірки задається параметром , тобто є однопараметричним. Інтегральна функція біноміального розподілу характеризується співвідношенням , де – найбільше ціле, що не перевищує число .

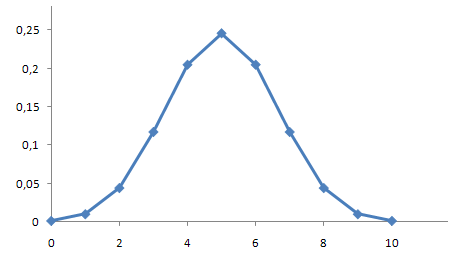
а) б)

Рис.7. Функція ймовірності біноміального розподілу

Математичне сподівання біноміального розподілу (6) дорівнює , дисперсія , асиметрія , ексцес .

Біноміальний розподіл застосовується при аналізі даних вибіркових досліджень, зокрема, при вивченні переваг споживачів, вибірковому контролі якості продукції за планами одноступінчастого контролю, при випробуваннях сукупностей індивідуумів у демографії, соціології, медицині, біології.

1.2.3. Розподіл Пуассона

Цей розподіл названий на честь французького математика С.Д.Пуассона, що вперше одержав його в 1837 р. (сам термін був уперше використаний Сопером в 1914 р.).

Розподіл Пуассона є граничним випадком біноміального розподілу, коли ймовірність здійснення події мала , але число випробувань велике. Тому розподіл Пуассона часто називають також «законом рідких подій».

Розподіл Пуассона виникає в теорії потоків подій. Доведено, що для найпростішого потоку з постійною інтенсивністю число подій (викликів), що відбулися за час , має розподіл Пуассона з параметром . Отже, імовірність того, що за час не відбудеться жодного події, дорівнює , тобто функція розподілу довжини проміжку між подіями є експонентною.

Функція ймовірності випадкової величини, що розподілена за законом Пуассона (див. рис.8), має вигляд

, (7)

а інтегральна функція задається рівністю . Тут параметр Пуассона.

Рис.8. Функція ймовірності розподілу Пуассона

Закон Пуассона (7) характеризується властивістю рівності математичного сподівання і дисперсії.

Характеристики цього закону є такими: математичне сподівання , дисперсія , асиметрія , ексцес .

Розподіл Пуассона моделює випадкову величину, що представляє собою число подій, які відбулися за фіксований час, за умови, що дані події відбуваються з деякою постійною середньою інтенсивністю і незалежно одна від одної. Розподіл Пуассона відіграє ключову роль у теорії масового обслуговування. Він використовується також при аналізі результатів вибіркових маркетингових обстежень споживачів, розрахунку оперативних характеристик планів статистичного приймального контролю у випадку малих значень приймального рівня дефектності, для опису числа розладнань статистично керованого технологічного процесу в одиницю часу, числа «вимог на обслуговування», що надходять в одиницю часу в систему масового обслуговування, статистичних закономірностей нещасних випадків і рідких захворювань. При розподіл Пуассона переходить у нормальний закон, відповідно до центральної граничної теореми.