Численные методы решения задач теплопроводности при нестационарном режиме

Для решения нестационарных задач численным методом из дифференциального уравнения теплопроводности

(1)

следует получить для каждого узла сетки уравнения в конечных разностях в виде:

,

где Т₀ – температура в точке 0 в момент t; Т₀ – температура в точке 0 через время Dt.

Тогда уравнение в конечных разностях:

если Dх = Dу = Dz = D, то

.

Откуда:

Эта формула позволяет по известной температуре Т₀ в данный момент времени t и в данной точке 0 и температурам Т₁,…Т₆ в момент t найти неизвестную температуру Т₀ в точке 0, но в следующий момент времени t + Dt.

Подбирая определенным образом шаг D и Dt, можно добиться устойчивости решения.

Лекция № 6

Метод конечных элементов

Решение задач теплопроводности может быть получено ещё одним численным методом – методом конечных элементов (МКЭ). Преимущества: математической основой метода является вариационное исчисление. В отличие от МКР, в котором исходные дифференциальное уравнения непосредственно используются для построения разностных схем, в МКЭ дифференциальное уравнение теплопроводности и соответствующие граничные условия используются для постановки вариационной задачи, которая затем решается численно. Этот метод нашел весьма широкое распространение благодаря своей универсальности. С его помощью решают не только задачи теплопроводности, но и рассчитывают конструкции на прочность, решают задачи электродинамики, гидравлики и т.д. Широко используют МКЭ в системе САПР.

Рассмотрим основы МКЭ. Пусть требуется найти стационарное распределение температуры Т(х, у) в двумерной области G с границей S. Для изотропного материала и при учете внутренних источников теплоты математическая постановка задачи в дифференциальной форме имеет вид: S a; T_¥

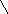
. (1)

Граничное условие на границе S:

, (2)

где l - коэффициент теплопроводности; q_v – объемное тепловыделение; Q – поверхностная плотность теплового потока; a - коэффициент теплоотдачи; T_¥ - температура окружающей среды.

В вариационном исчислении установлено, что решение Т(х, у), удовлетворяющее условиям (1) и (2) совпадает с функцией Т(х, у), которая минимизирует функционал

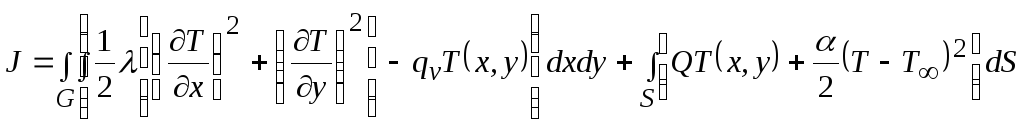,(3)

где G – рассматриваемая область; S – наружная поверхность, в которой имеет место теплоотдача; Т(х, у) – функция из допустимого множества пробных функций. Для задач теплопроводности пробные функции Т(х, у) является допустимыми, если они непрерывны и имеют кусочно-прерывные производные. Кроме того, пробные функции должны удовлетворять главным граничным условиям (2).

Таким образом, функционал (3) является эквивалентной вариационной постановкой исходной задачи (1) – (2).

Основными этапами решения данной задачи с помощью МКЭ является следующее: 1) Вначале область решения разбивается на конечное число подобластей, называемых конечными элементами. Выбор размеров и формы элементов в общем случае произволен. Элементы для плоского тела обычно имеют треугольную или четырехугольную форму. 2) Разбиение области решения на конечные элементы и условия непрерывности, накладываемые на пробные функции, позволяют записать функционал (3) в виде суммы функционалов по элементам

, (4)

где J_i – функционал вида (3) для i – го конечного элемента; к

n – число конечных элементов.

3). На каждом конечном элементе температура Т(х, у) аппроксимируется пробной i j

функцией Т(х, у). В качестве пробных функций обычно выбираются полиномы различных степеней. Например, температуру в элементе можно выразить в виде (линейно зависит от координат):

,

где T_i, T_j, T_k – температуры в узлах треугольного элемента; N_i, N_j, N_k – функции формы, зависящие от координат узлов.

Значение температуры в узлах сетки являются искомыми, поэтому для получения приближенного решения задачи необходимо «отрегулировать» эти значения температур таким образом, чтобы обеспечить минимум функционала (4). Условием минимума функционала является равенство нулю первых производных от него по температурам во всех узлах сетки

,

где .

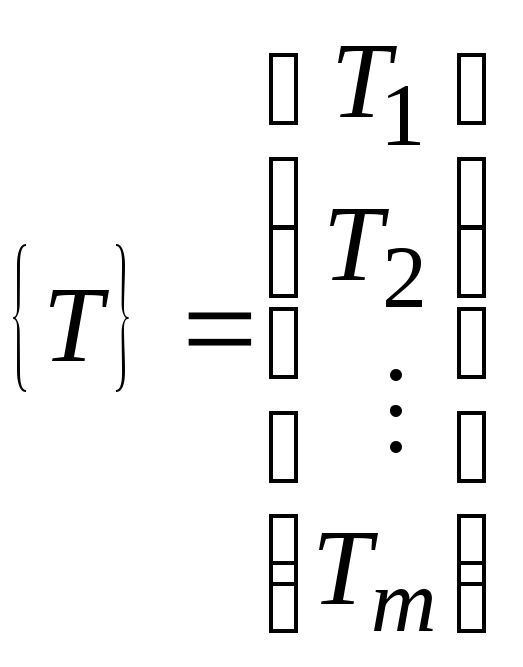В результате дифференцирования по всем неизвестным температурам получается система линейных алгебраических уравнений. В матричной форме она имеет вид

,

где и - матрица теплопроводности зависит от n и вектор нагрузки элемента (зависит от Q, q_v и граничных условий); - вектор узловых температур.

Последующее решение этой системы уравнений с помощью ЭВМ дает приближенное решение исходной задачи.

К достоинствам МКЭ относится простота аппроксимации тел со сложной геометрической формой и сложными граничными условиями.

Недостатком можно считать относительную сложность программирования для ЭВМ и применение ЭВМ с большим объемом оперативной памяти.

Лекция № 6