
Теоретические основы электротехники-3
.pdf
Глава 27. Магнитное поле постоянных токов |
161 |
27.18. Магнитное поле контура произвольной формы на большом расстоянии от контура
Обозначим через r расстояние точки M, в которой отыскивается потенциал Uì, от некоторой точки Î внутри контура (рис. 27.23). Пусть r много больше линейных размеров контура. Пусть ON — направление от Î ê M, при котором при заданном r телесный угол ! получается наибольшим, равным !max. При всяком другом направлении, составляющем с этим направлением угол ,
ïðè òîì æå r будем иметь ! !max cos . Íî !max s/r2, ãäå s — часть поверхности сферы радиуса r, вырезаемая центральным
конусом с телесным углом !max. Таким образом, согласно выражению Uì 4i ! , имеем
|
|
Ðèñ. 27.23 |
||||
U |
|
|
is |
|
cos |
. |
ì |
|
|
||||
|
|
4 r 2 |
||||
|
|
|
||||
Для плоского контура при r, намного большем размеров контура, s есть площадь, ограниченная контуром, и ON — направление нормали к ней.
Так как произведение is m есть магнитный момент тока i в замкнутом контуре, то формулу для Uì можно представить в виде
U |
|
|
m cos |
. |
ì |
|
|||
|
|
4r 2 |
||
|
|
|
||
Составляющие напряженности поля на больших расстояниях от контура
имеют выражения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
U ì |
|
|
2m cos |
; |
||||||
r |
r |
|
|
||||||||||
|
|
|
|
|
|
4r 3 |
|||||||
|
|
|
|
|
|
|
|||||||
H |
1 |
|
U ì |
|
m sin |
. |
|||||||
|
|
|
|||||||||||
|
|
|
|
r |
|
|
|
4 r 3 |
|||||
Из изложенного вытекает следующее важное положение. На больших расстояниях от контура тока напряженность магнитного поля убывает обратно пропорционально кубу расстояния, и характер поля совершенно не зависит от формы контура тока. Напряженность поля полностью определяется магнитным моментом.
Весьма интересно отметить, что характер магнитного поля на больших расстояниях от контура тока такой же, как и характер электрического поля диполя на больших от него расстояниях. Это становится ясным, если сопоставить полу- ченные в настоящем параграфе формулы с формулами в § 24.2 для поля электрического диполя.
27.19. Тело во внешнем магнитном поле. Аналогия с электростатической задачей
Задача о расчете магнитного поля при наличии во внешнем магнитном поле тела из вещества с абсолютной магнитной проницаемостью аналогична рассмот-

162 Часть 4. Теория электромагнитного поля
ренной в §§ 24.18 и 24.19 задаче о расчете электрического поля при наличии во внешнем электрическом поле тела из диэлектрика с абсолютной диэлектриче- ской проницаемостью .
Действительно, как уравнения поля, так и граничные условия аналогичны в обоих случаях.
Для магнитного поля имеем во всей интересующей нас области пространства rot H 0, так как в этой области отсутствуют макроскопические токи. Следовательно, уравнения магнитного поля имеют вид
rot H 0; B H 0 H 0 M; divB 0.
В соответствующей электростатической задаче в рассматриваемой области пространства div D 0, так как в этой области нет свободных зарядов. Поэтому уравнения электрического поля имеют вид
rot E 0; D E 0 E P; divD 0.
Заметим, что уравнения rot H 0 è rot E 0 эквивалентны уравнениям
H gradU ì è E gradU.
Граничными условиями на поверхности тела, внесенного во внешнее магнитное поле, являются равенство в обоих средах нормальных составляющих вектора магнитной индукции и касательных составляющих вектора напряженности поля:
Bn1 Bn2 è H t1 H t 2 .
Для тела из диэлектрика, внесенного во внешнее электрическое поле, гранич- ные условия имеют аналогичный вид:
Dn1 Dn2 è E t1 E t 2 .
Таким образом, при исследовании поля тел во внешнем магнитном поле можем воспользоваться аналогичными задачами, решенными в электростатике, с заменой E íà H, D íà B, P íà 0 M è íà . Так как поляризованность вещества P dp/dV, а намагниченность M dm/dV, то в аналогичных задачах электриче- ский момент соответствует умноженному на 0 магнитному моменту.
27.20. Шар и эллипсоид вращения во внешнем однородном магнитном поле
В § 24.19 был рассмотрен шар из диэлектрика, находящийся во внешнем электрическом поле. Было найдено, что шар поляризуется однородно.
Точно так же шар из вещества с абсолютной магнитной проницаемостью , помещенный во внешнее однородное магнитное поле, поляризуется однородно. Пусть шар помещен в пустоте и > 0. Тогда вектор напряженности H? поля, определяемого намагниченностью шара, оказывается внутри шара направленным против вектора напряженности H0 внешнего поля. В этом случае поле вектора H? называется р а з м а г н и ч и в а ю щ и м п о л е м. Используя формулы,

Глава 27. Магнитное поле постоянных токов |
163 |
полученные в § 24.19, и произведя в них соответствующую замену, получим формулы для интересующего нас случая. Напряженность размагничивающего поля определяется формулой
H |
? |
|
0 |
|
H |
|
. |
|
|
|
0 |
||||||
|
|
2 |
|
|
|
|
||
|
|
|
0 |
|
|
|
||
Вне шара поле, вызванное намагниченностью шара, такое же, как поле тока в весьма малом замкнутом контуре, находящемся в центре шара, имеющего магнитный момент m, равный геометрической сумме магнитных моментов всех элементарных токов в объеме шара.
Пользуясь формулами, полученными в § 24.19, находим
0 m 40 R3 H ? 4R3 0 0 2 0 0 H 0 ,
ãäå R — радиус шара.
Намагниченность M вещества шара равна магнитному моменту, отнесенному к единице объема шара. Следовательно,
|
|
M |
0 m |
3 |
|
0 |
|
H |
|
3 |
|
H |
? |
. |
|||
0 |
|
0 2 |
|
0 |
0 |
||||||||||||
|
|
4 |
R |
3 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Результирующая напряженность и результирующая магнитная индукция
внутри шара равны: |
|
|
|
|
|
|
|
|
|
|
|
|
H H 0 |
H ? |
|
3 |
0 |
|
H 0 ; |
|
|
||||
0 |
2 |
0 |
|
|
||||||||
|
|
|
|
|
|
|
|
|||||
B |
|
3 |
|
0 H 0 |
|
|
3 |
|
B0 . |
|||
|
|
|
|
|
|
|
||||||
0 |
2 |
0 |
0 2 |
0 |
||||||||
|
|
|
|
|
||||||||
Чем больше , тем сильнее размагничи- |
|
|
|
|
|
|||||||
вающее поле и тем слабее поле H, íî òåì |
|
|
|
|
|
|||||||
сильнее поле B. В пределе при . имеем |
|
|
|
|
|
|||||||
H ? H 0 ; H 0; B 3B0 . |
|
|
|
|
|
|
|
|||||
Таким замечательным свойством намаг- |
|
|
|
|
|
|||||||
ничиваться однородно во внешнем однород- |
|
|
|
|
|
|||||||
ном поле обладает эллипсоид, частным слу- |
|
|
|
|
|
|||||||
чаем которого является шар. На рис. 27.24 |
|
|
|
|
|
|||||||
для эллипсоида изображены внешнее одно- |
|
|
|
|
|
|||||||
родное поле, поле вектора H, определяемое |
|
|
|
|
|
|||||||
намагниченностью эллипсоида и связанное |
|
|
|
|
|
|||||||
с условным представлением о наведенных |
|
|
|
|
|
|||||||
магнитных массах, результирующее поле |
|
|
|
|
|
|||||||
вектора H и результирующее поле вектора B. |
|
|
|
Ðèñ. 27.24 |
||||||||

164 Часть 4. Теория электромагнитного поля
27.21. Магнитное поле в неоднородной среде. Применение метода интегральных уравнений
Решение задачи расчета магнитного поля в неоднородной среде становится полностью аналогичным соответствующей задаче электростатики при введении в рассмотрение магнитных зарядов объемной и поверхностной плотностью ì
èì, эквивалентных создающим поле токам.
|
|
|
|
|
|
|
Для расчета магнитного поля постоянного тока, |
||||||||||
|
|
|
|
|
|
протекающего в области V со средой, имеющей |
|||||||||||
|
|
|
|
|
магнитную проницаемость e, применим рассмот- |
||||||||||||
|
|
|
|
|
ренный в § 24.20 метод интегральных уравнений. |
||||||||||||
|
|
|
|
|
В части пространства, ограниченной замкнутой |
||||||||||||
|
|
|
|
|
поверхностью s, магнитная проницаемость опре- |
||||||||||||
|
|
|
|
|
деляется функцией i(x, y, z). Повторяя рассуж- |
||||||||||||
|
|
|
|
|
дения, выполненные в § 24.20 при введении вто- |
||||||||||||
|
|
|
|
|
ричных |
источников |
электростатического поля, |
||||||||||
|
Ðèñ. 27.25 |
|
|
|
и приводя среду к однородной с магнитной про- |
||||||||||||
|
|
|
|
ницаемостью e, получаем соотношения для плот- |
|||||||||||||
|
|
|
|
|
|||||||||||||
ности вторичных источников в виде (рис. 27.25) |
|
|
|
|
|||||||||||||
|
|
ì |
|
e |
|
H |
i |
grad |
i |
, |
ì |
2 |
H |
n |
, |
(*) |
|
|
|
|
|
||||||||||||||
|
|
|
i |
|
|
|
|
|
|
e |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ãäå Hn — нормальная к поверхности s составляющая напряженности магнитного
ïîëÿ, i e .i e
При расчете поля в кусочно-однородной среде по аналогии с интегральным уравнением (***), полученным в § 24.20, находим интегральное уравнение отно-
сительно размещенных на поверхности s магнитных зарядов плотностью |
ì: |
|||||||
|
|
|
|
ì cos(r, n) |
ds 2 |
e H |
0n . |
(**) |
ì |
2 |
r 2 |
|
|||||
|
|
|
s |
|
|
|
|
|
Свойства этого интегрального уравнения такие же, что и уравнения (***) § 24.20. При использовании скалярного магнитного потенциала и введении эквивалентных электрическим токам магнитных зарядов расчет входящей в правую часть уравнения (**) величины H0n становится полностью аналогичным расчету величины E0n в соответствующей задаче электростатики.
Правая часть уравнения (**) может быть выражена также и через создающие внешнее магнитное поле электрические токи, если для расчета напряженности
магнитного поля применить закон Био—Саварра. Рассчитывая величину H0n, öåëå- |
|||||||||||
сообразно сопоставить затраты на вычисление интеграла H0n |
|
|
|
|
1 |
|
|
|
ì dV |
||
n 4 |
|
r |
|||||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
e |
|
|
при замене токов магнитными зарядами и интеграла H0n |
1 |
|
|
[J, r]n |
|
dV , åñëè |
|||||
4 |
|
r 3 |
|||||||||
|
|
|
|
|
|||||||
|
|
|
V |
|
|
|
|
|
|
|
|
такая замена не выполняется.

|
|
|
|
|
|
|
|
|
|
Глава 27. |
Магнитное поле постоянных токов |
165 |
|||||||||
Изложенный подход можно применить для расчета как трехмерных, так и |
|||||||||||||||||||||
двухмерных магнитных полей. В случае плоскопараллельного поля входящая |
|||||||||||||||||||||
под знак интеграла |
функция в уравнении (**) будет иной, так как составляю- |
||||||||||||||||||||
щая напряженности магнитного поля, нормальная к контуру l сечения поверхно- |
|||||||||||||||||||||
сти раздела сред плоскостью X0Y, |
выражается формулой |
|
|
|
|||||||||||||||||
|
|
|
|
1 |
|
ìâ |
cos(r, n) |
|
|
1 |
|
|
|
cos(r, n) |
|
|
|||||
|
H n |
2 |
e |
|
|
r |
|
|
ds 2 |
e |
ì |
r |
|
dl, |
|
||||||
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
||
ãäå s — сечение плоскостью X0Y области с источниками внешнего поля, ìâ — |
|||||||||||||||||||||
объемная плотность магнитных зарядов, определяющих внешнее поле. |
|
||||||||||||||||||||
Уравнение (**) можно теперь записать в виде |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
ì |
cos(r, n) |
|
|
|
ìâ |
cos(r, n) |
|
|
|
|||||||
|
|
|
|
ì |
|
r |
|
|
dl |
|
|
|
r |
ds. |
|
|
|||||
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
Как отмечалось, применение векторного магнитного потенциала для расчета |
|||||||||||||||||||||
двухмерных магнитных полей так же эффективно, как и скалярного магнитного |
|||||||||||||||||||||
потенциала при преобразовании вихревых полей к потенциальным. Поэтому |
|||||||||||||||||||||
для расчета плоскопараллельного магнитного поля постоянного тока в кусоч- |
|||||||||||||||||||||
но-однородной среде в качестве вторичных источников используем размещен- |
|||||||||||||||||||||
ные на поверхности раздела сред электрические токи плотностью j. |
|
||||||||||||||||||||
Пусть контур l разделяет среды с магнитными проницаемостями i è e |
|||||||||||||||||||||
(ðèñ. 27.26). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Плотность j токов, расположенных на контуре |
|
|
|
|
|
||||||||||||||||
сечения тела с магнитной проницаемостью i, |
|
|
|
|
|
||||||||||||||||
должна быть выбрана так, чтобы обеспечить при |
|
|
|
|
|
||||||||||||||||
переходе к однородной среде с проницаемостью |
|
|
|
|
|
||||||||||||||||
скачок касательной составляющей магнитной ин- |
|
|
|
|
|
||||||||||||||||
дукции Bte |
e . Размещение на контуре l â îäíî- |
|
|
|
|
|
|||||||||||||||
Bti |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
родной среде с некоторой магнитной проницаемо- |
|
|
|
|
|
||||||||||||||||
стью слоя тока плотностью j (ñì. ðèñ. 27.26) âûçû- |
|
|
Ðèñ. 27.26 |
|
|||||||||||||||||
вает скачок касательных составляющих напряжен- |
|
|
|
||||||||||||||||||
|
|
|
|
|
|||||||||||||||||
ности магнитного поля Hti – Hte j и магнитной индукции Bti – Bte j. Обозначив |
|||||||||||||||||||||
через Bt касательную к контуру составляющую магнитной индукции в однород- |
|||||||||||||||||||||
ной среде, обусловленную всеми источниками за исключением расположенного в |
|||||||||||||||||||||
рассматриваемой точке, можем записать: Bte Bt – j, Bti |
Bt + j. Подставляя |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
эти выражения в соотношение Bte |
|
e , получаем после простых преобразова- |
|||||||||||||||||||
|
|
|
2 i e Bt |
Bti |
|
i |
|
|
|
|
|
|
|
|
|
|
|||||
ний уравнение j |
|
|
2 |
Bt, которое после подстановки величины |
|||||||||||||||||
|
|
|
i e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
B |
t |
A |
|
J' cos(r, n) ds |
|
j cos(r, n) dl |
|
|||||||||||||
|
|
|
n |
|
2 |
|
|
|
r |
|
|
2 |
|
r |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
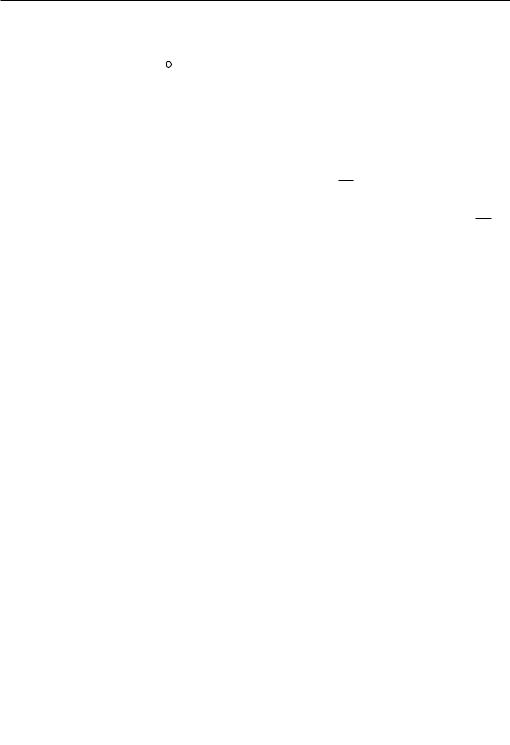
166 Часть 4. Теория электромагнитного поля
приводит к интегральному уравнению
j |
|
j |
cos(r, n) |
dl |
|
J' |
cos(r, n) |
ds. |
|
|
|
|
|||||
|
l |
r |
s |
r |
||||
|
|
|
|
|
|
|
||
Здесь s— сечение проводов с током плотностью J , задающим внешнее магнитное поле.
Если электрический ток, создающий внешнее магнитное поле, протекает в среде с магнитной проницаемостью i, то под входящей под знак интеграла плот-
ностью тока следует понимать величину, равную J i J. В случаях, когда электрический ток протекает в среде с магнитной проницаемостью e, имеем J e J.
Как и полученное выше уравнение (**), данное уравнение является интегральным уравнением относительно плотности вторичных источников и характеризуется аналогичными свойствами. Его решение может быть в некоторых случаях получено аналитически, однако в общем случае оно требует численного решения.
Найденное выше соотношение j (2 ) Bt можем использовать для расчета плоскопараллельного магнитного поля постоянного тока i, протекающего по прямолинейному проводу, расположенному в среде с магнитной проницаемостью 1 параллельно плоской поверхности раздела сред с магнитными проницаемостями1 è 2. Повторяя рассуждения, приведенные в § 24.23, найдем значения токов
) Bt можем использовать для расчета плоскопараллельного магнитного поля постоянного тока i, протекающего по прямолинейному проводу, расположенному в среде с магнитной проницаемостью 1 параллельно плоской поверхности раздела сред с магнитными проницаемостями1 è 2. Повторяя рассуждения, приведенные в § 24.23, найдем значения токов
i |
i |
2 |
1 |
i, |
i |
|
|
2 2 |
i. |
|
|
|
2 |
|
|||||||
1 |
|
2 |
1 |
|
|
2 |
1 |
|
||
|
|
|
|
|
|
|||||
Подобно зеркальному изображению в электрическом поле, для расчета магнитного поля в среде с магнитной проницаемостью 1 следует ввести зеркально изображенный ток i1 и после замены 2 íà 1 учесть токи i è i1 (ðèñ. 27.27, à). Для расчета поля в среде с магнитной проницаемостью 2 òîê i заменяем на i2, а магнитную проницаемость принимаем равной 2 во всем пространстве (рис. 27.27, á).
Ðèñ. 27.27

Глава 27. Магнитное поле постоянных токов |
167 |
27.22. Коэффициенты размагничивания
Для эллипсоидов как H?, òàê è M пропорциональны напряженности H0 внешнего поля. Стало быть, можно написать
H ? NM.
Коэффициент пропорциональности N называют к о э ф ф и ц и е н т о м р а з - м а г н и ч и в а н и я. От него зависит при данной намагниченности значение напряженности размагничивающего поля. Коэффициент размагничивания зависит только от формы намагничиваемого тела. Для шара получаем
N H ? 1 .
M 3
Расчет дает для эллипсоида вращения формулу
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arccos |
|
|
|
|
ln( 2 1) 1 |
|
1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||
N |
|
2 |
1 |
|
1 |
|
2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
, |
|||
|
|
|
2 1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 |
2 |
||||||
причем есть отношение оси вращения эллипсоида, которая предполагается направленной вдоль линии внешнего поля, к оси, ей перпендикулярной. Первым выражением для N удобно пользоваться при > 1, вторым — при < 1.
Для бесконечной, расположенной поперек поля пластины, которую можно рассматривать как сплющенный эллипсоид, находим N 1, приняв 0. Это — наивысшее возможное значение N. Для шара, полагая 1 и раскрывая неопределенность, получаем N 1 3. Для бесконечно длинного стержня, расположенного вдоль поля, полагая . и раскрывая неопределенность, получаем N 0.
3. Для бесконечно длинного стержня, расположенного вдоль поля, полагая . и раскрывая неопределенность, получаем N 0.
Свойство эллипсоидов однородно намагничиваться в однородном внешнем поле используется в магнитометрии. Для исследования магнитных свойств ферромагнитных материалов можно изготовить из этих материалов образцы, имеющие форму эллипсоида вращения или близкую к ней форму. Однородность намагничивания особенно важна именно при испытании ферромагнитных материалов, так как их магнитная проницаемость зависит от напряженности поля и только при однородном намагничивании значение во всем объеме образца будет одинаковым.
Ввести в рассмотрение коэффициент размагничивания, зависящий только от формы тела, строго говоря, возможно только для эллипсоидов и их частных слу- чаев: шара, пластины, бесконечно длинного цилиндра с эллиптическим или круглым сечением. Однако для приближенных практических расчетов магнитного поля, которое образуется при внесении в однородное внешнее поле тел иной формы, например коротких цилиндров, все же вводят в расчет коэффициенты размагничивания таких тел. Такой расчет является только ориентировоч- ным, так как тела, отличные по форме от эллипсоидов, намагничиваются неоднородно в однородном внешнем магнитном поле.
168 Часть 4. Теория электромагнитного поля
27.23. Магнитное экранирование
Для защиты электроизмерительных приборов от влияния посторонних магнитных полей их системы помещают в массивные замкнутые или почти замкнутые оболочки из ферромагнитного материала. Такие оболочки называют м а г н и т н ы м и э к р а н а м и. Поле внутри экрана оказывается ослабленным по сравнению с внешним полем.
Для экрана в форме полого шара с радиусами R1 è R2 (рис. 27.28) и с абсолютной магнитной проницаемостью стенок , помещенного во внешнее однородное поле с индукцией B0, магнитная индукция B в полости экрана мо-
Ðèñ. 27.28 |
жет быть рассчитана и оказывается равной |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B B0 |
|
|
|
|
|
1 |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
R3 |
|
|
|
|
|
|
||
|
|
|
|
0 |
|
|
|||||||
|
|
1 |
|
|
1 |
1 |
|
|
|
|
2 |
||
|
|
3 |
|
|
|
||||||||
|
|
|
9 |
|
|
|
|
|
0 |
|
|||
|
|
|
|
|
R2 |
|
|
|
|||||
Например, если R1 0,9R2 è 5000, òî B 0,031B0, т. е. напряженность поля внутри экрана составляет 3 % от напряженности внешнего поля. Для ферромагнитного вещества 00 0, и экранирующее действие определяется тем, что ли-
нии магнитной индукции внешнего поля, стремясь пройти по пути с наименьшим магнитным сопротивлением, сгущаются внутри стенок экрана, почти не проникая в его полость.
Нередко применяют многоступенчатые экраны в виде нескольких полых ферромагнитных тел, расположенных одно внутри другого.
27.24. Расчет магнитного поля в неоднородной среде методом конечных разностей
Численный расчет магнитного поля постоянных токов в неоднородной среде можно выполнить методом конечных разностей аналогично расчету электростатиче- ского поля. Аналогия решения уравнений Лапласа и Пуассона будет полной, если выполнить эквивалентную замену электрических токов магнитными зарядами плотностью ì. Численный расчет трехмерного магнитного поля целесооб-
разно выполнять, заменяя электрические токи магнитными зарядами, так как в этом случае вместо векторного уравнения можно перейти к решению скалярного
уравнения для скалярного магнитного потенциала. Для
формирования конечно-разностных уравнений воспользуемся соотношением
gradU ds |
U ds m (m — магнитный заряд). |
|
s |
s |
n |
|
||
|
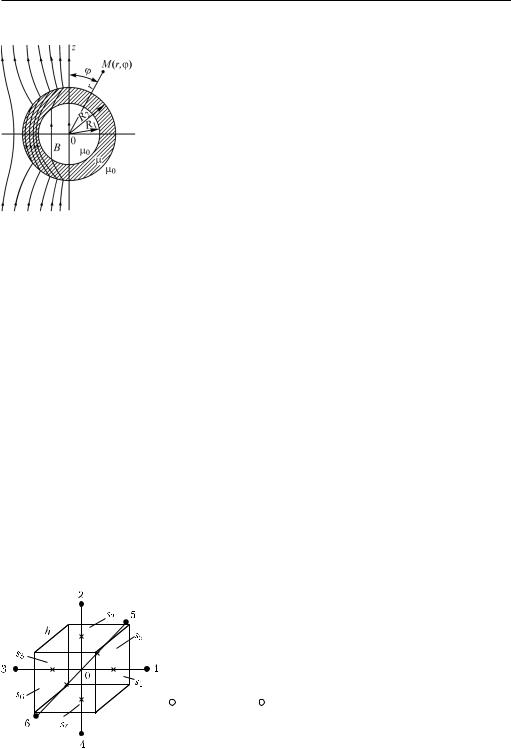
Разобьем рассматриваемый объем V на совокуп- |
Ðèñ. 27.29 |
ность одинаковых кубов с длиной ребра h (ðèñ. 27.29). |
|

|
Глава 27. Магнитное поле постоянных токов 169 |
|
Разместим магнитный заряд m в центре 0 куба и представим интеграл |
|
U ds по поверхности s куба в виде суммы шести интегралов по поверхно- |
s |
n |
|
ñòÿì s1, s2, …, s6 и вычислим их приближенно:
(x, y, z) grad xU ds Φ (1ñð h 2 |
0ñð h 2 ) |
U1 U 0 |
|
k1(U1 U 0 ), |
|||
|
|
||||||
s1 |
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
(x, y, z) grad yU ds Φ ( 2ñð h 2 |
0ñð h 2 ) |
U 2 |
U 0 |
k2 (U 2 |
U 0 ), |
||
|
h |
||||||
s2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x, y, z) grad zU ds Φ ( 6ñð h 2 |
0ñð h 2 ) |
U 6 |
U 0 |
k6 (U 6 |
U 0 ). |
||
|
h |
||||||
s6 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Здесь величины 1ñð, 2ñð, …, 6ñð являются средними функций (x, y, z) в соответствующих кубах.
Конечно-разностное уравнение
i 6 |
(*) |
k1U1 + k2U2 + … + k6U6 – U02ki – ìñð h3, |
|
i 1 |
|
в котором ìñð m/h3, выражает потенциал U0 узла 0 через потенциалы соседних шести узлов. Совокупность таких уравнений образует систему, которая может быть разрешена относительно искомых потенциалов узлов.
При численном расчете плоскопараллельного магнитного поля в неоднородной среде получим разностное уравнение относительно векторного магнитного потенциала, принимая за исходное соотношение H dl i. При этом исключает-
l |
|
|
|
|
|
|
|
|
|
|
|
|
ся необходимость перехода от токов к эквивалентным им |
|
|
|
|
|
|
|
|
|
|
|
|
магнитным зарядам. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разобьем область на совокупность квадратов с длиной |
|
|
|
|
|
|
|
|
|
|
|
|
стороны h. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
На рис. 27.30 изображены четыре смежных квадрата, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в каждом из которых магнитные проницаемости 1, …, 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и плотности J1, …, J4 тока имеют в общем случае различ- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ные значения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
Вычислим интеграл B dl вдоль контура abcd, äëÿ |
Ðèñ. 27.30 |
|
|
|
||||||||
l
чего разобьем его на четыре интеграла по сторонам ab, bc, cd, da контура:
|
B |
|
h |
|
|
h |
|
A |
0 |
A |
|
|
|
|
|
|
|
|
|
|
||
|
dl Φ |
|
|
|
|
|
|
|
|
1 |
|
k |
(A |
|
|
A ), |
||||||
|
|
|
|
|
|
|
|
|
|
0 |
||||||||||||
|
|
2 4 |
|
|
2 |
|
|
|
h |
|
1 |
|
|
1 |
|
|
||||||
ab |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
B |
|
h |
|
|
h |
|
A |
0 |
A |
2 |
|
k |
|
|
|
|
A |
|
|
||
|
dl Φ |
|
|
|
|
|
|
|
|
|
|
|
(A |
|
|
), |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
|||||||||
|
|
2 1 |
|
2 |
|
|
|
h |
|
2 |
|
|
|
|
||||||||
bc |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||

170 Часть 4. Теория электромагнитного поля
|
B |
|
h |
|
h |
|
A |
0 |
A |
3 |
|
|
|
|
|
|
|
dl Φ |
|
|
|
|
|
|
|
k |
(A |
|
A |
), |
|||
|
|
|
|
|
|
|
|
0 |
||||||||
|
|
2 2 |
|
2 |
|
|
|
h |
|
3 |
|
3 |
|
|||
cd |
|
|
3 |
|
|
|
|
|
|
|
|
|||||
|
B |
|
h |
|
h |
|
A |
0 |
A |
4 |
k |
|
|
A |
|
|
|
dl Φ |
|
|
|
|
|
|
|
(A |
|
). |
|||||
|
|
|
|
|
|
|
|
0 |
||||||||
|
|
2 4 |
|
2 |
|
|
|
h |
|
4 |
|
4 |
|
|||
da |
|
|
3 |
|
|
|
|
|
|
|
|
|||||
Входящий в разностное уравнение (A0 – A1) k1 + (A0 – A2) k2 + (A0 – A3) k3 + + (A0 –A4) k4 i òîê i сквозь площадку, ограниченную контуром abcda, выразим через плотности J1, …, J4 тока в квадратах i Φ Jñð h2 0,25 ( J1 + J2 + J3 + J4) h2 и получим окончательно:
4 |
4 |
(**) |
2ki Ai |
A0 2ki Jñð h 2 . |
|
i 1 |
i 1 |
|
По аналогии с разностными уравнениями (*) уравнения (**), записанные для совокупности ячеек сетки, образуют систему алгебраических уравнений, решение которой позволяет определить векторный потенциал в совокупности точек области.
